FWT(快速沃尔什变换)

文章目录

- 引入：
- or卷积
- and卷积
- xor卷积
- IFWT
- 模板：
- 例题：

引入：

FFT/NTT是用来解决 $∑i+j=kA[i]B[j]\sum_{i+j=k}A[i]B[j]$ 的式子
而FWT是用来解决 $Ci=∑j⊕k=iAj×BkC_i=\sum_{j⊕k=i}A_j×B_k$

FWT是一种用于处理位运算卷积的算法
证明我也不是很懂，网上有很多讲的详细的，这里只讲应用：
现在有一些卷积，形如：
$Ck=∑i∨j=kAi∗BjC_k=\sum_{i ∨ j=k}A_i∗B_j$
$Ck=∑i∧j=kAi∗BjC_k=\sum_{i ∧ j=k}A_i∗B_j$
$Ck=∑i⨁j=kAi∗BjC_k=\sum_{i \bigoplus j=k}A_i∗B_j$
普通的FFT就没辙了，就要用到FWT来做，我们直接给出结论：

or卷积

我们把多项式A $2^n项)$ 拆成两部分 $A_0,A_1$ ,则有：
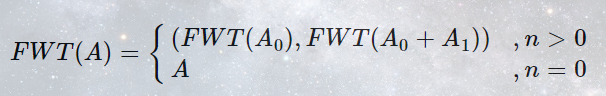
在这里插入图片描述
然后把上面的部分是指两部分合到一块
还有个性质： $FWT(A)i=∑j∨i=iAjFWT(A)_i=\sum_{j∨i=i}A_j$
所以统计子集和可以用FWT

and卷积

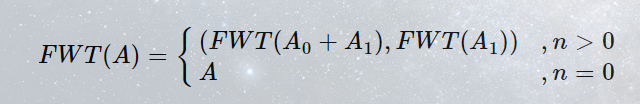
在这里插入图片描述
性质： $FWT(A)i=∑j∧i=iAjFWT(A)_i=\sum_{j∧i=i}A_j$
统计超集和

xor卷积

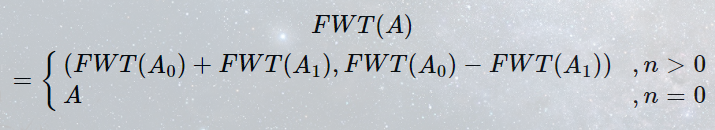
在这里插入图片描述

IFWT

有FWT，就要再变换回来，还要有IFWT
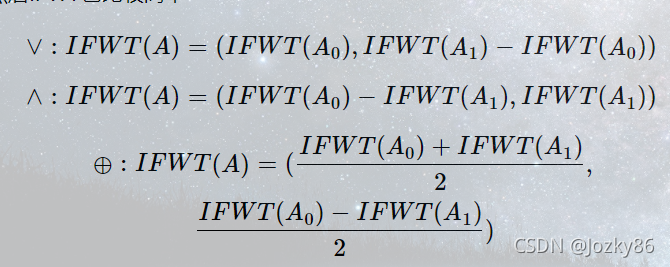
在这里插入图片描述
主要是会应用就行

模板：

#include <cstdio>
typedef long long ll;
const int mod=998244353;const int N=1<<20;
int a[N],b[N],c[N];
ll qpow(ll a,ll b){ll ans=1;while(b){if(b&1)ans=ans*a%mod;a=a*a%mod;b>>=1;}return ans%mod;
} 
void FWT(int x[],int t1,int t2,int len)
{const ll inv2= qpow(2,mod-2);for(int i=1;i<len;i<<=1)for(int j=0;j<len;j+=(i<<1))for(int k=0;k<i;k++){ll p=x[j+k],q=x[i+j+k];if(t1==0) x[i+j+k]=(q+mod+t2*p)%mod;  //orelse if(t1==1) x[j+k]=(p+mod+t2*q)%mod;   //andelse if(t1==2)   //xor{x[j+k]=(p+q)%mod*(t2<0?inv2:1)%mod;x[i+j+k]=(p+mod-q)%mod*(t2<0?inv2:1)%mod;}     }
}
int main()
{int n;scanf("%d",&n);
//    int len=2;int len=(1<<n);for(int i=0;i<len;i++) scanf("%d",&a[i]);for(int i=0;i<len;i++) scanf("%d",&b[i]);for(int t=0;t<3;t++){FWT(a,t,1,len);FWT(b,t,1,len);//相对应的运算 for(int i=0;i<(1<<n);i++) c[i]=(1LL*a[i]*b[i])%mod;FWT(a,t,-1,len);FWT(b,t,-1,len);FWT(c,t,-1,len);for(int i=0;i<(1<<n);i++) printf("%d%c",c[i],i<(1<<n)-1?' ':'\n');}return 0;
}