Visual Studio容器项目工程化心得

引言　　

　　关注博主的网友会看到我使用ASP.NET Core 容器化部署企业级项目的过程，回想到开发过程中，鄙人有一些工程化心得，分享给同学们。

项目工程化

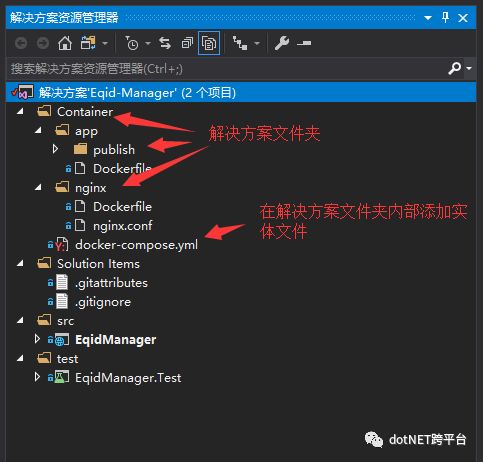
　　因为本项目涉及单元测试Project、容器化部署、本地化的sqlite数据库，nlog日志，因此有必要给出我的Visual Studio 2019 解决方案目录：

需要理解几点：

① 建立container文件夹

　　该专门存放容器化部署相关的文件，将开发内容和部署内容分开是一种DevOps实践，同时也为我们以后实现CI/CD做些许铺垫。

　　小技巧：在使用Visual Studio的时候，可建立与以上文件件同名的解决方案文件夹，这样便于开发人员编写部署脚本。

640?wx_fmt=png

② 编写git ignore 文件

　　网上很多大牛分享过git的操作技巧，add, commit, push, checkout、merge 相信很多开发人员烂熟如心。

但是作为企业级工程，多少会涉及一些不需要代码仓库管理的文件（密钥文件、临时文件、本地数据库文件、日志文件），这就涉及git ignore的用法，更丰富的官方文档在这里： https://git-scm.com/docs/gitignore

这个操作很多时候是由架构师一次性配置完成，很多开发同学没有实操过，今天我们也来玩弄一下。

// 在解决方案.sln 同级目录下编写的.gitignore文件：忽略vs user file,nuget package,temp files
 *.suo
*.user
packages
.vs
.nuget
container/app/publish/*

//  在EqidManager项目文件夹下编写.gitignore文件：忽略localdb,logs,temp files
*.suo
*.user
bin
obj
internal-nlog.txt
EqidManager.db
healthchecksdb

640?wx_fmt=jpeg

③ 编写WebDeploy Publish Profile

　　container文件夹中包含app和nginx的镜像准备文件和对应的Dockerfile，这里我们关注 app/publish文件夹, 里面将会存放本次应用程序的最终可执行文件。

使用WebDeploy部署的时候，在该路径生成部署文件，便于统一管理，产生的FolderPublish.pubxml 如下：

<?xml version="1.0" encoding="utf-8"?>
<!--
此文件由 Web 项目的发布/打包过程使用。可以通过编辑此 MSBuild 文件
自定义此过程的行为。为了解与此相关的更多内容，请访问 https://go.microsoft.com/fwlink/?LinkID=208121。 
-->
<Project ToolsVersion="4.0" xmlns="http://schemas.microsoft.com/developer/msbuild/2003">
  <PropertyGroup>
    <WebPublishMethod>FileSystem</WebPublishMethod>
    <PublishProvider>FileSystem</PublishProvider>
    <LastUsedBuildConfiguration>Release</LastUsedBuildConfiguration>
    <LastUsedPlatform>Any CPU</LastUsedPlatform>
    <SiteUrlToLaunchAfterPublish />
    <LaunchSiteAfterPublish>True</LaunchSiteAfterPublish>
    <ExcludeApp_Data>False</ExcludeApp_Data>
    <ProjectGuid>1213badd-176e-4c24-af84-bfdb0517b692</ProjectGuid>
    <publishUrl>../../container/app/publish</publishUrl>
    <DeleteExistingFiles>False</DeleteExistingFiles>
  </PropertyGroup>
</Project>

<!--
  关注黄色背景行，发布目录使用相对路径（相对于项目文件***.csproj的路径）
-->