1. 什么是 JWT

JWT 其全称为：JSON Web Token，简单地说就是 JSON 在 Web 上的一种带签名的标记形式。官方的定义如下：

JSON Web Tokens are an open, industry standard RFC 7519 method for representing claims securely between two parties.

即：JSON Web Token (JWT)是一个开放标准(RFC 7519)，它定义了一种紧凑的、自包含的方式，用于作为JSON对象在各方之间安全地传输信息。

2. 有什么作用

对信息进行签名之后再进行传输有什么作用，JWT 就有什么作用。它能起的作用，决定了在项目的需求中是否有必要使用它，它自身的本质决定了它适合的场景。

本质上，JWT 跟自己对信息加个签名没有区别。

那使用它的理由是什么呢？

（1）它建立了一个标准并为多数人认识和接受，这样一来就可以形成标准库，使用者可以共享。

（2）它形成了一些最佳实践，这种实践过程包括了参数安全传递的诸多常见方面，如 exp 到期时间属性的定义来规定签名有效期等。按照最佳实践中对一些 JSON 属性的明确定义，再加上标准库对它的贯彻实现，会带来很多便利。

（3）将其作为 Token 放在请求的 header 中，作为无状态的鉴权方式很适合目前多站点应用的场景。

但最佳实践和其特性不能混为一谈，具体到应用场景，仍然可以利用其特性作适合该场景的其它发挥。

3. 参数访问控制演化

（1）直接传参

http://*/api?p1=*&p2=*

这种方式，不进行访问的权限的判断，公开可直接访问。

（2）带KEY传参

http://*/api?p1=*&p2=*&key=

这种方式需要知道正确的 KEY 才能访问，但 KEY 明文附在后面易泄露。

（3）带签名传参

这种方式，将 KEY 作为签名算法的加密条件，不明文显示，不知道 KEY 则无法生成相应的签名，感觉不错。不足在于，签名一次之后访问链接一直为有效会带有风险。

http://*/api?p1=*&p2=*&sign=

其中签名部分，如采用 md5 方式，key 作为运算的一部分。

sign=md5(p1+p2+key)

（4）带时间戳签名

参数中带上签名时的时间戳，时间戳会参与签名算法，服务端不仅检测签名的有效性，还会比较时间是否在合理范围内，如 5 分钟以内，如此一来，链接在一段时间之后就会失效。

http://*/api?p1=*&p2=*&timestamp=*&sign=

其中签名部分，如采用 md5 方式，time，key 均作为运算的一部分。

sign=md5(p1+p2+time+key)

（5）独立鉴权参数签名

将鉴权部分独立出来签名，这样的好处就是鉴权部分独立的判断过程，其它形参不再需要参与这个签名与判断过程。

参数可使用 JSON 形式，于是可以让其变成以下形式：

鉴权传输部分形式如：{p1:abcd,p2:abcd}.sign

其中，签名部分，如采用 md5 方式，将 JSON 字符串与 key 拼接运算，并且使用连接符.点，如下。

sign=md5({p1:abcd,p2:abcd}.key)

（6）带头部的独立鉴权部分

为了更加灵活的，将鉴权部分加个头部。头部用来干什么呢，可以指定签名算法，或以后可能要更多扩展参数用，如以下形式。

{alg:MD5}.{p1:abcd,p2:abcd}.sign

签名部分，为前两部分再连接上 key 一起运算。

sign=md5({alg:MD5}.{p1:,p2:}.key)

（7）最终标准化为 JWT 形式

头部称之为 header，数据部分称之为 payload，签名部分为 signature。

(7.1) header 不使用明文，采用其 base64 形式

(7.2) payload 不使用明文，采用其 base64 形式

(7.3) signature 为前两者（都是 base64 形式）通过 . 点连接，再采用 header 中指定的签名算法签名的结果。

(7.4) 最终形式为 base64(header).base64(payload).signature

(7.5) base64 考虑到URL编码，将=去掉，+号变成-，/变成_ 处理。

(7.6) 最终字符串通过作为请求 header 进行传输。

4. 最简实现

给定一个签名用的 sercretKey 和 payload，生成成符合要求的 JWT 字符串。多数时候，需求可能就是这样简单，至于签名算法，这里就使用一般默认的HS256。则需要的功能函数大致是：

func getJwt (payload){    var content = base64({"alg":"HS256","typ":"JWT"}) + . + base64(payload)    var signature = base46( sign(content, sercretKey)  )    return content + . + sign}

C# 的实例代码，这里给出一个 C# 的 JWT 辅助类，其中 JObject 引用了 Newtonsoft.Json 包。

    public class JWTHelper    {        #region 工具函数准备        public static string Base64URL(string str)        {            return Convert.ToBase64String(Encoding.UTF8.GetBytes(str)).Replace("=", "").Replace("+", "-").Replace("/", "_");        }                public static string Base64URL(byte[] bs)        {            return Convert.ToBase64String(bs).Replace("=", "").Replace("+", "-").Replace("/", "_");        }        public static string HS256(string str, string key)        {            var encoding = new System.Text.UTF8Encoding();            byte[] keyByte = encoding.GetBytes(key);            byte[] messageBytes = encoding.GetBytes(str);            using (var hmacsha256 = new HMACSHA256(keyByte))            {                byte[] hashmessage = hmacsha256.ComputeHash(messageBytes);                return Base64URL(hashmessage);            }        }        #endregion                public static string Sign(JObject payload, String key)        {            JObject header = new JObject();            header["alg"] = "HS256";            header["typ"] = "JWT";            string h = Base64URL(header.ToString(Formatting.None));            string p = Base64URL(payload.ToString(Formatting.None));            string s = HS256(h + "." + p, key);            return String.Format("{0}.{1}.{2}", h, p, s);        }    }

使用以下代码测试一下：

JObject payload = new JObject();payload["username"] = "xxx";Console.Write(JWTHelper.Sign(payload, "123fd"));

得到结果

eyJhbGciOiJIUzI1NiIsInR5cCI6IkpXVCJ9.eyJ1c2VybmFtZSI6Inh4eCJ9.1C28A5CqMa70FLtUQh4pwSZWPlZhbQ-ZeYs38K_sqks

在 https://jwt.io/ 上，可以验证一下，得到了同样的结果。

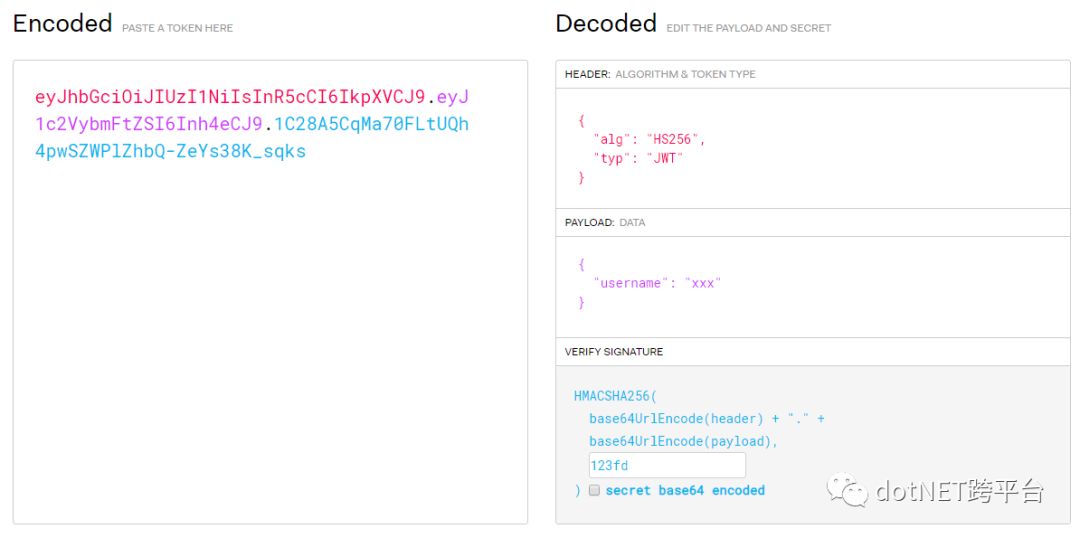
5. 具体使用

显然，它也会存在一些问题，如通过 base64 解码看到明文，或者是在有效期内取得整个 token 进行访问等。所以使用是根据需要来的。而且，也可以在 JWT 上进一步加入自定义的新机制来应对更多的场景。

以下这篇文章列出了一些问题与趋势，可供参考。

https://baijiahao.baidu.com/s?id=1608021814182894637

更多细节可参考：https://www.cnblogs.com/cjsblog/p/9277677.html