传送门

题意：一个$x\in (-\infty ,+\infty ),y\in [0,R]$的矩形中有$n$个点，矩形外有$m$个半径均为$R$的圆，有独立的代价$c_i$。求覆盖最多的点所需的最小代价。

$n,m\le 100$

显然先把永远不可能覆盖到的点扔掉，然后转化为覆盖所有点

先考虑圆心都在矩形上方的情况

结论 对于一个合法（即覆盖所有点）的圆的集合，一定存在一个圆和点的匹配方式，使得每个圆匹配的点是按照$x$排序后的一段。

证明

考虑排序后的一段点，如果一个圆覆盖了左边和右边的点，而中间的点没有覆盖

类似于这样：

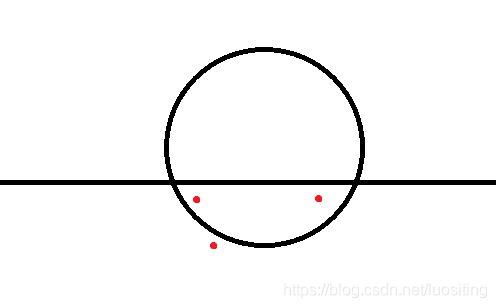
（红色的是点）

因为下面的点保留下来了，所以一定有一个圆覆盖它 假设这个圆在当前圆的圆心的左边，在右边同理

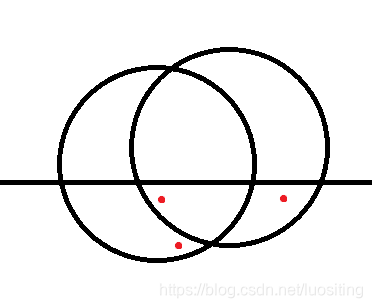
看上去它覆盖了左边的点，所以接下来我们的证明就往这个方向努力

注意到两个圆的半径都是$R$,所以两个圆交点所在的直线是两个圆心的中垂线

而两个圆心都在直线上方，所以连线的中点也在直线上方，所以中垂线一定和圆有一个直线上的交点，这个可以用反证法证明。

这样根据意识流，右边的圆 左边的部分一定被左边的圆覆盖了

如果圆半径不相同，就会出现这样的情况：

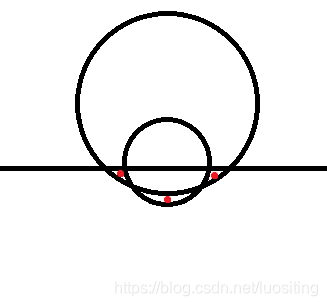
然后是一个很憨的dp

设$dp(i,j,k)$表示当前处理到排完序后的第$i$个点，上面的圆上次处理的是第$j$个，下面是第$k$个(因为上面的结论只对一边有效，所以两边要分别处理)

转移的时候是如果当前点在上/下面的圆内

1. 可能上一个点也用了这个圆，这个点接在后面
2. 可能上一个点用的是其他圆

注意圆不用排序，因为第二、三个参数的含义是上次处理“了”这个圆，这次可能会接着处理来找到最优解，而不是处理“到”这个圆，所以圆的坐标会反复横跳。

dp过程中实际上有很多方案并不满足每个圆对应一段（因为没有也没法判断这个圆是否用过），但这些方案一定不是最优解（因为同一个圆被算了多次代价，但实际上即使我们去重之后也可以达到相同的效果），同时满足限制的都被统计入答案了，所以可以找到最优解。

复杂度$O(n^4)$

#include <iostream>
#include <cstdio>
#include <cstring>
#include <cctype>
#include <algorithm>
#define MAXN 105
using namespace std;
inline int read()
{int ans=0,f=1;char c=getchar();while (!isdigit(c)) f=(c=='-'? -1:1),c=getchar();while (isdigit(c)) ans=(ans<<3)+(ans<<1)+(c^48),c=getchar();return f*ans;                                                                                                                                                                                                                                                                                                                                                                                                       
}
typedef long long ll;
const int INF=0x3f3f3f3f;
int R;
struct point{int x,y,c;}s[MAXN],w[MAXN],up[MAXN],low[MAXN];
inline bool check(const point& a,const point& b){return (ll)(a.x-b.x)*(a.x-b.x)+(ll)(a.y-b.y)*(a.y-b.y)<=(ll)R*R;}
inline bool operator <(const point& a,const point& b){return a.x==b.x? a.y<b.y:a.x<b.x;}
int cnt1,cnt2;
int dp[MAXN][MAXN][MAXN];
int main()
{int n,m;n=read(),m=read(),R=read();for (int i=1;i<=n;i++) s[i].x=read(),s[i].y=read();for (int i=1;i<=m;i++) w[i].x=read(),w[i].y=read(),w[i].c=read();int tot=0;for (int i=1;i<=n;i++)for (int j=1;j<=m;j++)if (check(s[i],w[j])){s[++tot]=s[i];break;}sort(s+1,s+tot+1);for (int i=1;i<=m;i++)if (w[i].y<0) low[++cnt2]=w[i];else up[++cnt1]=w[i];for (int i=0;i<=cnt1;i++)for (int j=0;j<=cnt2;j++)dp[0][i][j]=INF;dp[0][0][0]=0;for (int k=1;k<=tot;k++)for (int i=0;i<=cnt1;i++)for (int j=0;j<=cnt2;j++){dp[k][i][j]=INF;if (i&&check(up[i],s[k])) {dp[k][i][j]=min(dp[k][i][j],dp[k-1][i][j]);	for (int l=0;l<=cnt1;l++) dp[k][i][j]=min(dp[k][i][j],dp[k-1][l][j]+up[i].c);}if (j&&check(low[j],s[k])) {dp[k][i][j]=min(dp[k][i][j],dp[k-1][i][j]);	for (int l=0;l<=cnt2;l++) dp[k][i][j]=min(dp[k][i][j],dp[k-1][i][l]+low[j].c);}}int ans=INF;for (int i=0;i<=cnt1;i++)for (int j=0;j<=cnt2;j++)ans=min(ans,dp[tot][i][j]);printf("%d\n%d\n",tot,ans);return 0;	
}