这里是Z哥的个人公众号

每周五11：45 按时送达

当然了，也会时不时加个餐～

我的第「87」篇原创敬上

Hi，大家好，我是Z哥。

熟悉我的小伙伴应该知道，我平时看书大多都很快，之前还把自己的速读技巧分享给了大家。（我珍藏5年的10倍速阅读法）

今年截止到现在，我已经看了30多本书了。但是，最近的一个多星期我只看了一本书，郭建龙老师的《中央帝国的财政密码》。因为我在速读完一遍之后，又细细品味了一遍。

这本书真的太棒了，让我有一种豁然开朗的感觉。我觉得值得每个人去读一下。

通过书中讲述的中国两千多年的经济发展的演变趋势，会让你对我们当下的社会经济，有更进一步的理解和认识。让你身处在“庐山”之中，也能识到“庐山”的真面目。

据说这本书写了7年，为了力求引用内容的准确、真实，作者翻阅了《史记》、《战国策》、《周礼》、《春秋左传》等等67本正史，阅读量惊人。

我在此书中的收获颇多，就不一一赘述了。你看，记了一堆内容。

就挑几个让我感受深刻的点展开说一下。顺带也分享一下我自己的一些进一步的思考和观点。

感受1

刚读了这本书的1/3之后，你就会发现当今社会中的诸多现象和问题，在历史上都有过相似的一幕。甚至有些还不止一次。

我们当下社会中的企业、组织的经营和治理其实有很多方面和国家的治理是互通的。

这也解释了为什么那些商场、官场的大佬们，都对历史颇有研究的原因。

因为里面藏着大量的实践经验，特别是那些失败的经验，导致国家走向衰落、走向灭亡的经验。这些都可以帮助我们在当下少走很多弯路。

虽然说世事无绝对，一种做法不可能一直对，也不可能一直错，毕竟所处的环境在变化。但错过了一个做对的机会还能等下一个，而做出了一个错的决定，则有可能再也等不到下一个机会了。

之前在朋友圈发了一张图，也是对这点的有感而发。

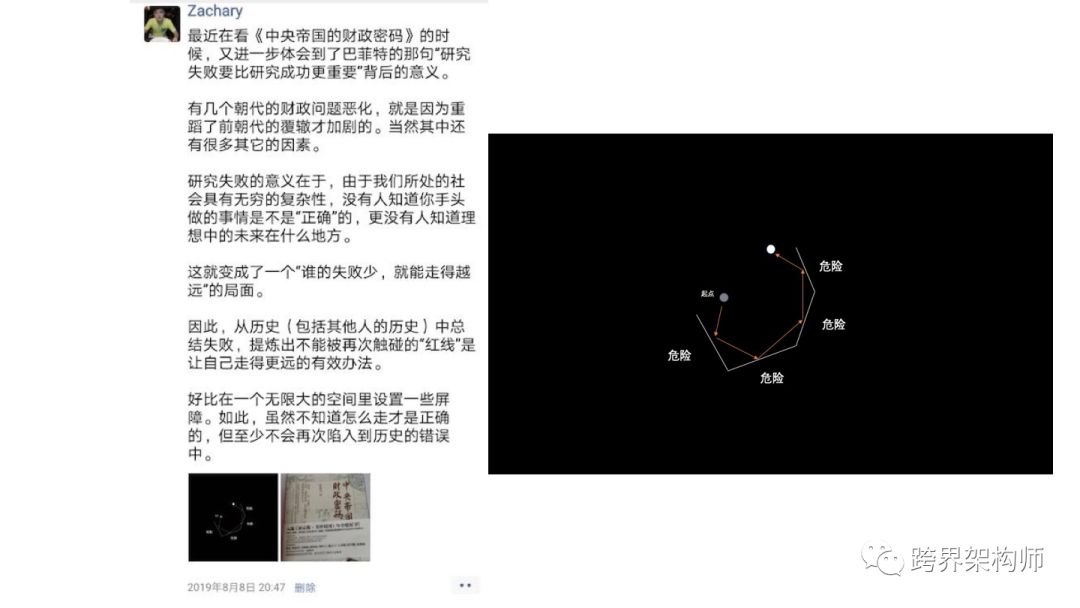
感受2

我们身边有很多人是理想主义者，Z哥我也是。

在理想主义者的世界里，做一件事往往只有一条路，就是那条“最完美”的路。

但其实我们永远要记得「上有政策下有对策」。一个再完美的想法，执行下去必有衰减，甚至会发生背道而驰的情况。

所以，我们务必要在进行方案制定、规划安排、落实措施等工作的时候，多考虑一些“坏情况”的发生。

我前几天还和身边的理想主义小伙伴说，我们要“抱着最好的理想，做着最坏的准备”。如果你也是理想主义者，也可以试试。

感受3

很多看上去很正确的事，如果真的按照100%的要求彻底执行，可能反而会适得其反。

比如，纳税对国家很重要，但是100%按户籍纳税反而会吃力不讨好。

因为灰色地带的「模糊性」背后体现的是「灵活性」。为了彻底消灭灰色地带，执行起来反而会变得更加的“机械化”，很容易会陷入到为了追求某个指标去做事。

那么怎么来考虑？Z哥建议你从“边际产出”的角度来考虑。

当我要做一件事，从80%做到90%可能是值得的，投入产出是正的。但是当95%做到99%还值得吗？得好好慎重考虑一下，根据实际情况决定，不要一股脑的死干。

感受4

那些身处高位的人一定要定期到一线去，通过间接的、侧面的、局部的信息来验证自己所接收到的信息的「可信度」。

根据书中的记载，隋朝的官员上报给皇帝的数据，有些甚至被夸大10倍。比如，一个很容易判断的点，当时登记在册的土地面积比我们当前的国土面积还大……

皇帝在这样的大背景下做决策，错误必然比正确的多。

那么怎么才能改善甚至是避免呢，其实在之前的《一句话概括4本管理著作》中也有提到一些。

• 用书面报告代替口头陈述。

• 偶尔深入问一些细节作为“抽查”。

感受5

一个人或者组织，其实和软件系统一样，所处的位置越底层，稳定性越是第一位的。（职业病，习惯性的喜欢和技术扯上关系：D）

比如，一个软件系统分硬件层面和软件层面，软件层面做的再好，硬件层面只要不稳定，全盘崩塌，这个软件的价值等于0。

这也是为什么越基础的事物发展的越慢，因为对它们来说，除了“快”，更重要的是“稳”。

所以，如果你所从事的工作是其他人的“下游”，那么不妨考虑一下，平时是否有把稳定性放在第一位？是不是有让别人觉得你靠谱？

感受6

以寻求共赢，一起把饼做大，一起分享做大的红利，才是可持续的发展道路。

如果我们以零和博弈的视角去做事，那不是你赢，就是我输。

假如止步于此，我们的社会其实是无法发展和进步的。因为整体的“总量”没有增加，蛋糕还是这么大。

甚至因为相互之间的内耗导致蛋糕更小了也有可能。

所以，我们平时在与其它人合作的时候，应该更多的去考虑，这个蛋糕我们可以一起做到多大？在做大的过程中，如何去分这个蛋糕，让大家都能享受到做大的好处？这二个问题很现实，但很重要。

我们这个时代新产生了很多岗位，并且越来越多的工作内容无法被客观的量化。这个情况还有愈演愈烈趋势。

如果用经济学中「剩余索取」的概念来考虑分蛋糕的问题，会是一个不错的办法。

在减去事先计划的支出和可量化部分的支出后，“剩的多，得的多；剩的少，得的少。”

感受7

Z哥我一直是将「事物皆有两面性」奉作最重要的理念去做事的，刚开这个公众号那会我还将它设置为关注自动回复中。

在阅读该书的过程中，有些事例让我对这个理念的认识得到了进一步的加强。

比如，我们现在每天在用的“人民币”这种法定货币，其实也是有利有弊的。虽然大家都喜欢它：D

最早的时候，人们交易用的都是自然货币，就是以实物作为货币，粮食、盐等等。

缺点很明显，就是假如我想用粮食换盐的话，必须得找一个正好想用盐换粮食的人才行。但是优势是人们在交易的时候自然会以它们的“实际价值”来作为交易价值的砝码，缺斤少两是很敏感的。

当以“面值”为交易价值的法定货币推出后，的确让交易更方便了。任何东西与货币做交换就好了，同时还能促进跨区域的交易。

但中央如果不具备统一铸币的能力，交由市场自行铸币，会催生“劣币驱逐良币”的问题。因为大家总会将足额的优质货币藏在家里，交易的时候先将那些掺加杂质的劣势货币用掉，导致市场中流通的都是劣质货币，并且越来越劣质。

解决的办法很简单，由中央统一铸币，统一规格。汉武帝就是这么干的。

但这也让中央通过铸币来间接地增加财富，成了一个方便之选。把0.5克铜当5克铜的价值来用，自然会催生通货膨胀问题。

这个问题在如今可能会更严重，原因你应该也能想到。

感受8

行政效率是一个组织得以持续生存的基本。

说起东汉这个朝代，可能大多数人的印象中只有那个三国之前的“东汉末年”，好像这个朝代的皇帝没什么作为啊。

其实主要的原因并不在皇帝本身，而是由于东汉继承的西汉行政体系太低效了，导致连皇帝想要做什么事，都推动不了。

在我们身边也能看到类似的现象。有些公司的发展陷入困境，想作出一些改变，但是不管是大的还是小的改革，推进困难，连老板都无可奈何，推动不了。

这其实和东汉的情况是一样的，行政体系已经僵化了。所以行政体系是一个组织的“循环系统”，运转不动了，离“挂”也就不远了。

感受9

为了解决某个眼前的问题，一旦临时开设“快捷方式”，往往会收不住手。因为短期利益的诱惑力实在太强了。

比如，唐肃宗为了方便筹钱，建立新的职位「租佣使」，这个职位在正统官员的体系之外。但随后，各种“使”开始不断出现，让正统官员形同虚设，权力失控。

所以，当我们冲着“图省事”去做一个决定的时候，冥冥之中其实就打开了一条通往“大坑”的“捷径”。一旦踩不住刹车，那等待你的只有是远处的“大坑”。

技术圈中，很多程序员对那些历史悠久的项目怨气很重，所谓“不堪入目的祖传代码”其实就是在每一个时期所作出的各种“捷径”的大集合。

因为在当时做出这个决定的时候，对决定者来说这是最省事的一个方案。

感受10

前面说到，唐肃宗为了筹钱，慢慢开始建立了很多“使”出来。

这么做的根本原因还是因为没钱，再加上正统官员体系的行政效率低，筹不到钱。

因为，财政是一个国家的命脉。

这和现在很多企业有钱的时候谈理想，没钱的时候不顾底线敛财的道理是一样的。

包括说为什么皇帝睁一只眼闭一只眼地倚重宦官？奸臣？原因还是因为能给他们带来钱。他们也知道这些钱的收取都是透支未来所得，是不可持续的。但毕竟活得过明天才能谈未来，也是逼不得已。

马斯洛的需求模型所表达的也是这个意思。

▲图片来源于网络，版权归原作者所有

这情况不但会出现在一个组织中，包括我们每个个体在决策的时候也是如此。

感受11

盯住基础科学的创新，这里面蕴藏着大量应用层面的创新机会。

宋代的雕版印刷术成熟促使了“飞钱”诞生。这也是我们现在用的纸币的起源。

在“飞钱”诞生之前，人们的交易成本是很高的。毕竟，身上揣着那么重的货币，没事谁愿意走的很远去做交易，或者多带一些在身上。

Z哥认为最近大火的AI、区块链、5G，本质上还是应用层面的创新，因为底层所用的东西还是那些老的事物。

像量子领域这种，假如能够进一步的突破，我认为才是真正意义上的基础科学的创新。

不知道你怎么看？

总结

今天这篇文章的内容比较散，但是「知识密度」比较高，可以多回味、思考一下。

希望对你有所启发。

如果你最近正好想找书看，不妨看一看这本，真的是强力推荐。

帮你搜了一下价格，如果凑单买的话京东便宜，单买的话当当便宜，下面请自取。

推荐阅读：

• 一句话概括4本管理著作

• 你会轻易打破规则吗？

原创不易，如果你觉得这篇文章还不错，就「在看」或者「分享」一下吧。鼓励我的创作 ：）

如果你有关于软件架构、分布式系统、产品、运营的困惑

可以试试点击「阅读原文」