经典排序算法（11）——计数排序算法详解

计数排序（Counting sort）是一个非基于比较的排序算法，该算法于1954年由 Harold H. Seward 提出。它的优势在于在对一定范围内的整数排序时，它的复杂度为Ο(n+k)（其中k是整数的范围），快于任何比较排序算法。

一、算法基本思想

（1）基本思想

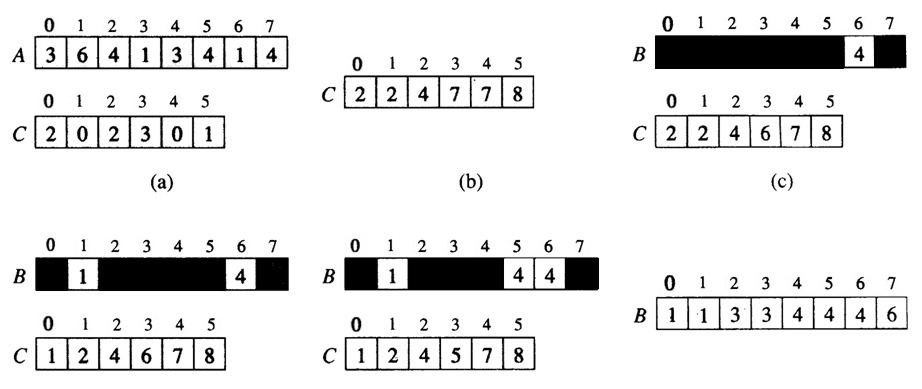
计数排序的基本思想是对于给定的输入序列中的每一个元素x，确定该序列中值小于x的元素的个数。一旦有了这个信息，就可以将x直接存放到最终的输出序列的正确位置上。

例如，如果输入序列中只有17个元素的值小于x的值，则x可以直接存放在输出序列的第18个位置上。当然，如果有多个元素具有相同的值时，我们不能将这些元素放在输出序列的同一个位置上。解决方案就是要反向填充目标数组，以及将每个数字的统计减去1。

（2）运行过程

计数排序的运行过程如下：

1、找出待排序的数组中最大和最小的元素；

2、统计数组中每个值为i的元素出现的次数，存入数组 C 的第 i 项；

3、对所有的计数累加（从C中的第一个元素开始，每一项和前一项相加）；

4、反向填充目标数组：将每个元素i放在新数组的第C(i)项，每放一个元素就将C(i)减去1。

（3）示例

二、算法实现（核心代码）

Java实现：

//针对c数组的大小，优化过的计数排序
public class CountSort{public static void main(String []args){//排序的数组int a[] = {3, 6, 4, 1, 3, 4, 1, 4};int b[] = countSort(a);for(int i : b){System.out.print(i + "  ");}System.out.println();}public static int[] countSort(int []a){int b[] = new int[a.length];int max = a[0], min = a[0];for(int i : a){if(i > max){max = i;}if(i < min){min = i;}}//这里k的大小是要排序的数组中，元素大小的极值差+1int k = max - min + 1;int c[] = new int[k];for(int i = 0; i < a.length; ++i){c[a[i]-min] += 1;//优化过的地方，减小了数组c的大小}for(int i = 1; i < c.length; ++i){c[i] = c[i] + c[i-1];}for(int i = a.length-1; i >= 0; --i){b[--c[a[i]-min]] = a[i];//按存取的方式取出c的元素}return b;}
}

三、性能（算法时间、空间复杂度、稳定性）分析