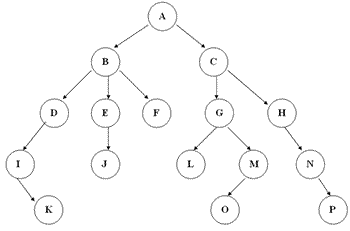
一、树的定义

树是由n（n>=1）个有限节点组成一个具有层次关系的集合，它有如下特点：

1、每个节点有零个或多个子节点；

2、没有父节点的节点称为根节点；

3、每一个非根节点有且只有一个父节点；

4、除了根节点外，每个子节点可以分为多个不相交的子树。

一棵树至少包含一个树节点，不存在不包含树节点的树。

树中节点的最大层次称为树的深度（或高度）。

二、二叉树的定义

二叉树是每个节点最多有两个子树的树结构。通常子树被称作“左子树”（left subtree）和“右子树”（right subtree）。

二叉树与树不同之处：

1、树的节点个数至少为1，而二叉树的节点个数可以为0；

2、树中节点的最大度数没有限制，而二叉树节点的最大度数为2；

3、树的节点无左、右之分，而二叉树的结点有左、右之分。

二叉树的性质：

1、在二叉树的第i层最多有2^(i-1)个节点（i≥1）；

2、深度为h的二叉树至多有2^h - 1个节点；

3、包括n（n>1）个元素的二叉树的边树为n-1；

4、对于任何一颗二叉树，若其叶子节点数记为n0，其度为2的节点数记为n2，则有n0 = n2+1。

5、若一颗满二叉树有n个节点，则其深度h应为h = log2(n)+1，对数取下限。

6、一颗有n个节点的完全二叉树，从左至右，从上至下，从1开始编号，对于编号为i的节点，有：

（1）若i=1，则i是根节点；若i≠1，则i/2是i的父亲；

（2）若2i≤n，则i的左孩子是2i；若2i＞n，则i没有孩子；

（3）若2i+2≤n，则i的右孩子是2i+1；若2i+1>n，则i没有右孩子。

二叉树的遍历方式：前根（根左右）、中根（左根右）、后根（左右根）遍历。

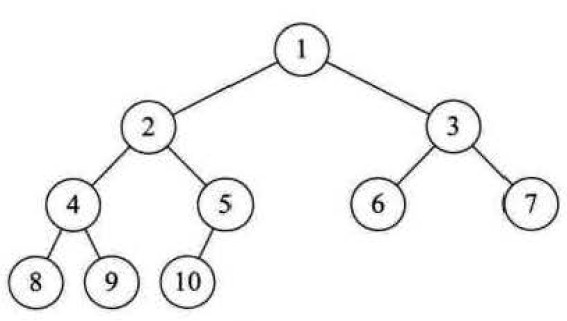
三、完全二叉树的定义

对于一颗二叉树，假设其深度为d（d>1）。除了第d层外，其它各层的节点数目均已达最大值，且第d层所有节点从左向右连续地紧密排列，这样的二叉树被称为完全二叉树。

在一棵二叉树中，除最后一层外，其余层都是满的，并且最后一层或者是满的，或者是在右边缺少连续若干节点，则此二叉树为完全二叉树。

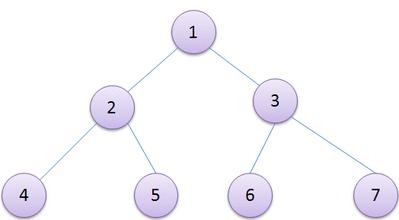
四、满二叉树的定义

一棵深度为k，且有2^k-1个节点的二叉树，称为满二叉树。

对于上述的完全二叉树，如果去掉其第d层的所有节点，那么剩下的部分就构成一个满二叉树（此时该满二叉树的深度为d-1）。

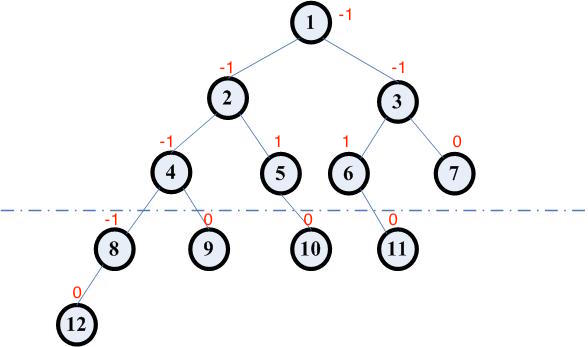
五、平衡二叉树的定义

平衡二叉树的定义如下：

1、它的左子树和右子树的高度之差的绝对值不超过1；

2、它的左子树和右子树都是平衡二叉树。

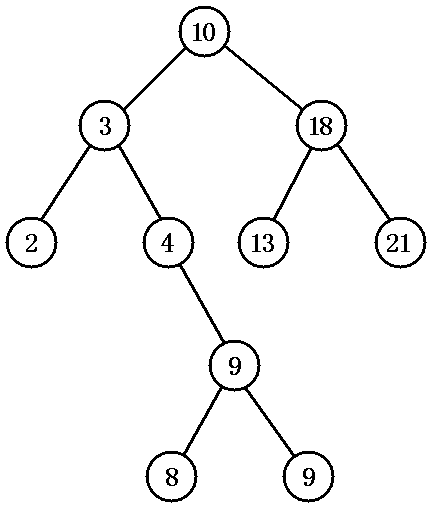
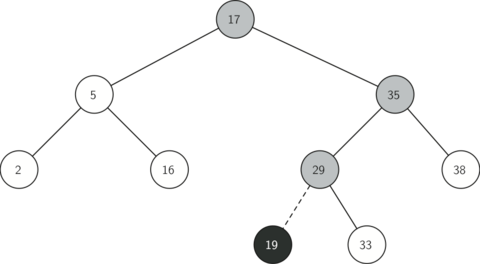
六、二叉搜索树的定义

二叉搜索树的定义如下：

1、任意节点的左子树不空，则左子树上所有结点的值均小于它的根结点的值；

2、任意节点的右子树不空，则右子树上所有结点的值均大于它的根结点的值；

3、任意节点的左、右子树也分别为二叉查找树；

4、没有键值相等的节点。

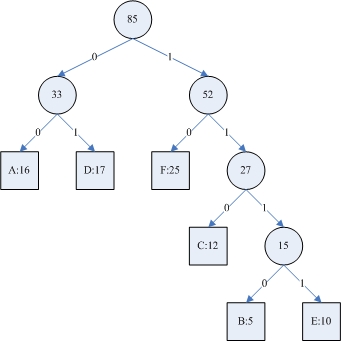
七、霍夫曼树的定义

霍夫曼树又称最优二叉树，是一种带权路径长度最短的二叉树。霍夫曼树的所有元素都在叶子节点上。

所谓树的带权路径长度，就是树中所有的叶结点的权值乘上其到根结点的路径长度（若根结点为0层，叶结点到根结点的路径长度为叶结点的层数）。