一、平衡二叉树的定义
平衡二叉树（Balanced Binary Tree）又被称为AVL树，它且具有以下性质：
（1）它是一棵空树或它的左右两个子树的高度差的绝对值不超过1；
（2）并且左右两个子树都是一棵平衡二叉树。
把二叉树的每个节点的左子树减去右子树定义为该节点的平衡因子。二叉平衡树的平衡因子只能是1、0或者-1。
需要注意的是，平衡二叉树是对二叉搜索树(又称为二叉排序树)的一种改进。二叉搜索树有一个缺点就是，树的结构是无法预料的，随意性很大，它只与节点的值和插入的顺序有关系，往往得到的是一个不平衡的二叉树。在最坏的情况下，可能得到的是一个退化（单支）二叉树，其高度和节点数相同，相当于一个单链表，对其进行查找的时间复杂度由O(logn)变成了O(n)，从而丧失了二叉排序树的一些应该有的优点。
二、平衡二叉树AVL调整
在平衡二叉树中删除或插入节点后，可能会使某些节点的平衡因子的绝对值大于 ，即树失去了平衡，这时候就需要进行平衡调整，使其重新满足平衡二叉树的要求。
调整平衡二叉树之前，首先要明白一个定义：最小不平衡子树。最小不平衡子树是指以离插入节点最近、且平衡因子绝对值大于1的节点做根的子树。
平衡二叉树的调整主要分为四种：
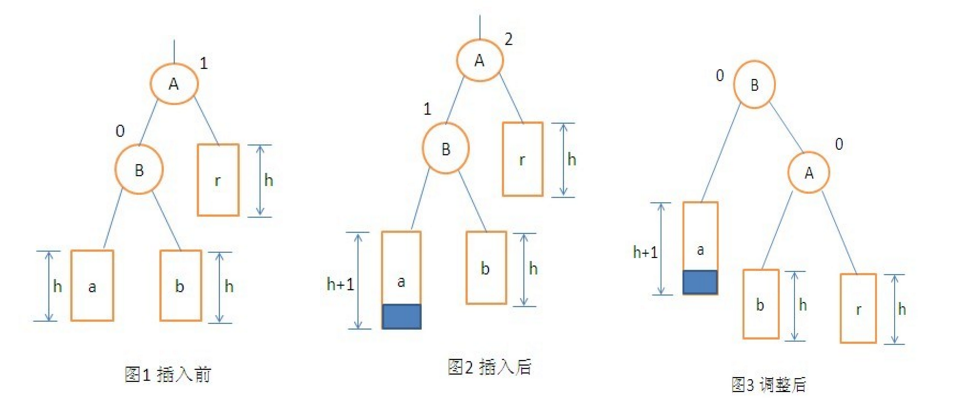
（1）单向右旋平衡处理LL：由于在*a的左子树根节点的左子树上插入节点，*a的平衡因子由1增至2，致使以*a为根的子树失去平衡，则需进行一次右旋转操作；
如下图所示：发生不平衡（平衡因子绝对值大于1）的节点和插入的节点在一条直线上，如同 / 状，则只需要进行一次向右旋转即可。旋转之后，不平衡节点的左孩子的右子树，需要移动到不平衡节点的左子树上。
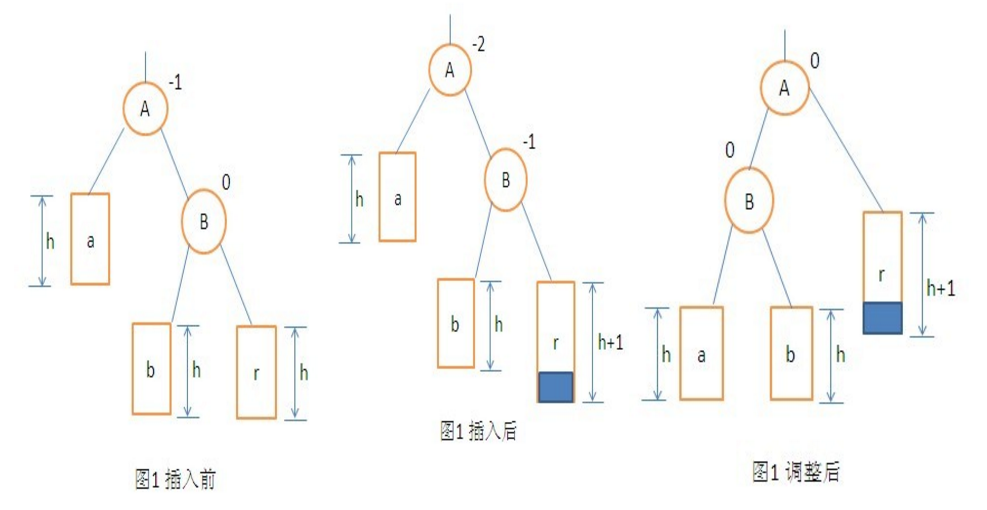
（2）单向左旋平衡处理RR：由于在*a的右子树根节点的右子树上插入节点，*a的平衡因子由-1变为-2，致使以*a为根的子树失去平衡，则需进行一次左旋转操作；
如下图所示：发生不平衡（平衡因子绝对值大于1）的节点和插入的节点在一条直线上，如同 \ 状，则只需要进行一次向左旋转即可。旋转之后，不平衡节点的右孩子的左子树，需要移动到不平衡节点的右子树上。
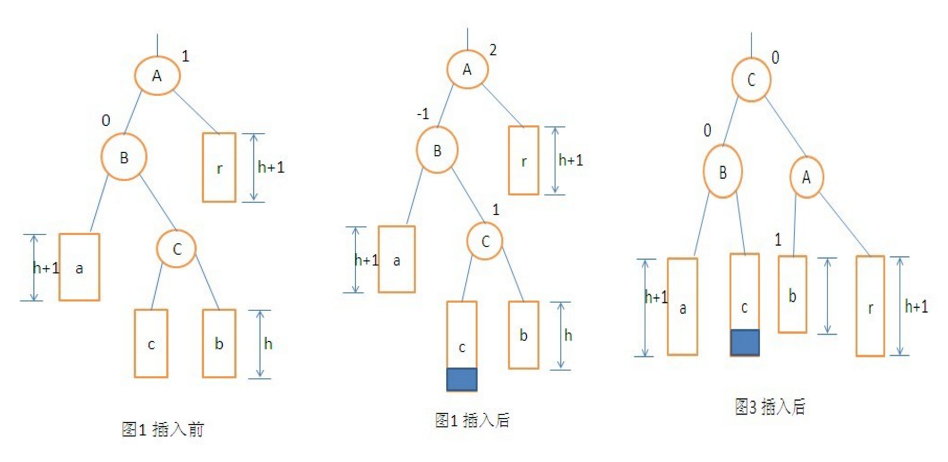
（3）双向旋转（先左后右）平衡处理LR：由于在*a的左子树根节点的右子树上插入节点，*a的平衡因子由1增至2，致使以*a为根的子树失去平衡，则需进行两次旋转（先左旋后右旋）操作。
如下图所示：发生不平衡（平衡因子绝对值大于1）的节点和插入的节点不在一条直线上，如同 < 状，则首先需要进行一次向左旋转，然后进行一次向右旋转。
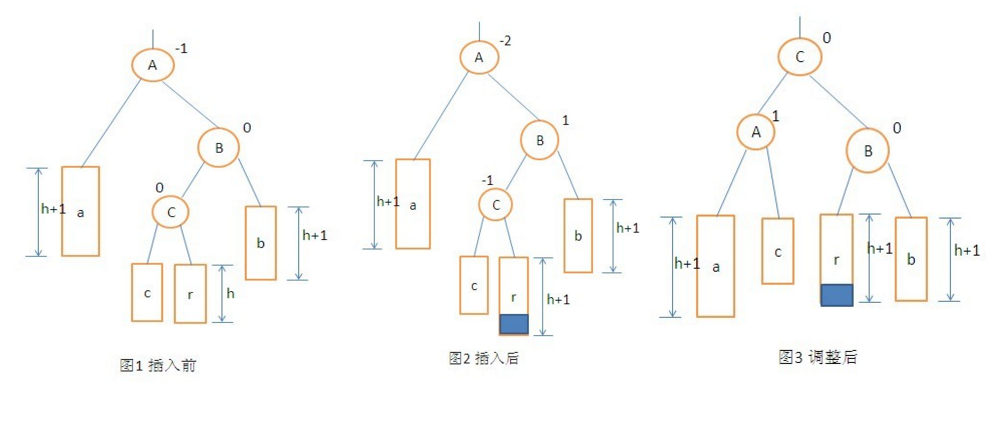
（4）双向旋转（先右后左）平衡处理RL：由于在*a的右子树根节点的左子树上插入节点，*a的平衡因子由-1变为-2，致使以*a为根的子树失去平衡，则需进行两次旋转（先右旋后左旋）操作。
如下图所示：发生不平衡（平衡因子绝对值大于1）的节点和插入的节点不在一条直线上，如同 > 状，则首先需要进行一次向右旋转，然后进行一次向左旋转。
