题目描述
如下面第一个图的九宫格中，放着 1~8 的数字卡片，还有一个格子空着。与空格子相邻的格子中的卡片可以移动到空格中。经过若干次移动，可以形成第二个图所示的局面。

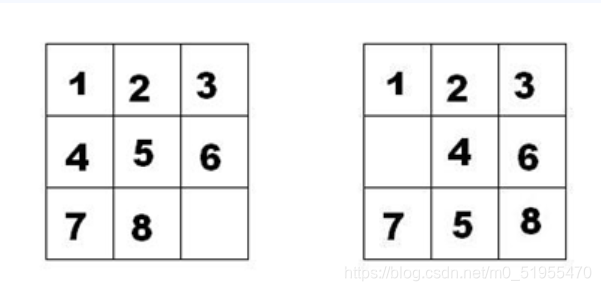
我们把第一个图的局面记为：12345678.
把第二个图的局面记为：123.46758
显然是按从上到下，从左到右的顺序记录数字，空格记为句点。
本题目的任务是已知九宫的初态和终态，求最少经过多少步的移动可以到达。如果无论多少步都无法到达，则输出-1。
输入
输入第一行包含九宫的初态，第二行包含九宫的终态。
输出
输出最少的步数，如果不存在方案，则输出-1。
样例输入
12345678.
123.46758
样例输出
3

普通的bfs超时了，只能拿67分。
代码如下：

#include <iostream>
#include <queue>
#include <map>
using namespace std;
int mp[4][4];
map<int, int>vis;
map<int, int>st; //step
int target  = 0;
int row, col;int dx[] = {0, 0, 1, -1}, dy[] = {1, -1, 0, 0};bool move_can(int u, int d) {for (int i = 2; i >= 0; i--)for (int j = 2; j >= 0; j--) {mp[i][j] = u % 10;u = u / 10;if (mp[i][j] == 0) {row = i;col = j;}}if ((d == 0 && col == 2) || (d == 1 && col == 0) || (d == 2 && row == 2) || (d == 3 && row == 0))return false;return true;
}int move_to(int u, int d) {int xx = row + dx[d];int yy = col + dy[d];mp[row][col] = mp[xx][yy];mp[xx][yy] = 0;int tmp = 0;for (int i = 0; i < 3; i++)for (int j = 0; j < 3; j++) {tmp = tmp * 10 + mp[i][j];}return tmp;
}int bfs(int s) {queue<int>q;vis[s] = 1;st[s] = 0;q.push(s);while (q.size()) {int t = q.front();q.pop();if (t == target)return st[t];for (int i = 0; i < 4; i++) {if (move_can(t, i)) {int v = move_to(t, i);if (!vis[v]) {vis[v] = 1;st[v] = st[t] + 1;q.push(v);}}}}return -1;
}int main() {int state = 0;for (int i = 0; i < 3; i++)for (int j = 0; j < 3; j++) {char c;cin >> c;if (c >= '1' && c <= '8')mp[i][j] = c - '0';elsemp[i][j] = 0;state = state * 10 + mp[i][j];}for (int i = 0; i < 9; i++) {char c;cin >> c;if (c >= '1' && c <= '8')target = target * 10 + (c - '0');else {int tmp = 0;target = target * 10 + tmp;}}cout << bfs(state) << endl;return 0;
}

然后我采用了双向bfs，然后ac了！

代码如下：

#include <iostream>
#include <queue>
#include <map>
using namespace std;
char c;
map<int, int>vis;
map<int, int>dis;
int mp[4][4];int dx[] = {0, 0, 1, -1}, dy[] = {1, -1, 0, 0};
int nx, ny;
int ans;void fff1(int s) {int div = 100000000;for (int i = 0; i < 3; i++)for (int j = 0; j < 3; j++) {mp[i][j] = (s / div) % 10;if (mp[i][j] == 0) {nx = i;ny = j;}div = div / 10;}
}int fff2() {int tmp = 0;for (int i = 0; i < 3; i++)for (int j = 0; j < 3; j++) {tmp = tmp * 10 + mp[i][j];}return tmp;
}int dbfs(int s, int e) {if (s == e)return 0;queue<int>q1, q2;q1.push(s), q2.push(e);vis[s] = 1, vis[e] = 2;dis[s] = 0, dis[e] = 1;while (q1.size() && q2.size()) {int t;bool flag;if (q1.size() < q2.size()) {t = q1.front();q1.pop();flag  = 1;} else {t = q2.front();q2.pop();flag = 0;}fff1(t);for (int i = 0; i < 4; i++) {int xx = nx + dx[i], yy = ny + dy[i];if (xx >= 0 && xx < 3 && yy >= 0 && yy < 3) {swap(mp[xx][yy], mp[nx][ny]);int v = fff2();if (!dis.count(v)) {dis[v] = dis[t] + 1;vis[v] = vis[t];if (flag)q1.push(v);elseq2.push(v);} else if (vis[v] + vis[t] == 3) {ans = dis[v] + dis[t];return ans;}swap(mp[xx][yy], mp[nx][ny]);}}}return -1;
}int main() {int s = 0;int e = 0;for (int i = 0; i < 9; i++) {cin >> c;if (c == '.')c = '0';s = s * 10 + (c - '0');}for (int i = 0; i < 9; i++) {cin >> c;if (c == '.')c = '0';e = e * 10 + (c - '0');}cout << dbfs(s, e) << endl;return 0;
}