对于代价函数:
loss=∑i(y^−yi)2loss=\sum_i{(\hat{y}-y_i)}^2loss=∑i(y^−yi)2
loss=∑i(w∗xi+b−yi)2loss=\sum_i{(w*x_i+b-y_i)}^2loss=∑i(w∗xi+b−yi)2
最常见的代价函数:均方差代价函数(Mean-Square Error,MSE):
loss=12N∑iN(w∗xi+b−yi)2loss=\frac{1}{2N}\sum_i^N{(w*x_i+b-y_i)}^2loss=2N1∑iN(w∗xi+b−yi)2
一 梯度下降(Gradient Descent)
在学习梯度下降原理之前首先我们需要知道这几个数学概念:导数、偏导数、方向导数和梯度。关于梯度下面直接说结论:
- 梯度是一个矢量,既有大小又有方向
- 梯度的方向是最大的方向导数
- 梯度的值是方向导数的最大值
梯度下降算法基本原理:
既然在变量空间的某一点处,函数沿着梯度方向具有最大的变化率,那么在优化代价函数的时候,就可以沿着负梯度方向去减小代价函数的值。
梯度下降数学原理:
w′=w−lr∗∂loss∂ww\prime=w-lr*\frac{\partial loss}{\partial w}w′=w−lr∗∂w∂loss
b′=b−lr∗∂loss∂bb\prime=b-lr*\frac{\partial loss}{\partial b}b′=b−lr∗∂b∂loss
其中lr表示的是学习率:LearningRate
""""
用一元线性回归解决回归问题: y = wx + b
"""
import numpy as np
import matplotlib.pyplot as plt
# 画图正常显示中文
plt.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False # 用来正常显示负号def compute_error(b, w, points):totalError = 0for i in range(0, len(points)):x = points[i, 0]y = points[i, 1]# computer mean-squared-errortotalError += (y - (w * x + b)) ** 2# average loss for each pointreturn totalError / float(len(points))def step_gradient(b_current, w_current, points, learningRate):b_gradient = 0w_gradient = 0N = float(len(points))for i in range(0, len(points)):x = points[i, 0]y = points[i, 1]# 计算梯度 grad_b = 2(wx+b-y) grad_w = 2(wx+b-y)*xb_gradient += (2 / N) * ((w_current * x + b_current) - y)w_gradient += (2 / N) * x * ((w_current * x + b_current) - y)# update w'new_b = b_current - (learningRate * b_gradient)new_w = w_current - (learningRate * w_gradient)return [new_b, new_w]def gradient_descent_runner(points, starting_b, starting_w, learning_rate, num_iterations):b = starting_bw = starting_w# update for several timesfor i in range(num_iterations):b, w = step_gradient(b, w, np.array(points), learning_rate)return [b, w]def plot_scatter(data):x_data = data[:, 0]y_data = data[:, 1]plt.scatter(x_data, y_data)plt.title("训练数据集散点分布")plt.xlabel("自变量:x")plt.ylabel("因变量:y")plt.savefig("scatter.png")# plt.show()def plot_result(data, w, b):x_data = data[:, 0]y_data = data[:, 1]plt.scatter(x_data, y_data, c='b')plt.plot(x_data, w * x_data + b, 'r')plt.title("训练拟合结果")plt.xlabel("自变量:x")plt.ylabel("因变量:y")plt.savefig("result.png")# plt.show()def run():# numpy读取CSV文件points = np.genfromtxt("data.csv", delimiter=",")# 绘制数据散点图plot_scatter(points)# 设置学习率learning_rate = 0.0001# 权值初始化initial_b = 0initial_w = 0# 迭代次数num_iterations = 1000print("Starting b = {0}, w = {1}, error = {2}".format(initial_b, initial_w,compute_error(initial_b, initial_w, points)))print("Running...")[b, w] = gradient_descent_runner(points, initial_b, initial_w, learning_rate, num_iterations)print("After {0} iterations b = {1}, w = {2}, error = {3}".format(num_iterations, b, w, compute_error(b, w, points)))plot_result(points, w, b)if __name__ == '__main__':run()
运行结果:
Starting b = 0, w = 0, error = 5565.107834483211
Running…
After 1000 iterations b = 0.08893651993741346, w = 1.4777440851894448, error = 112.61481011613473
数据集:
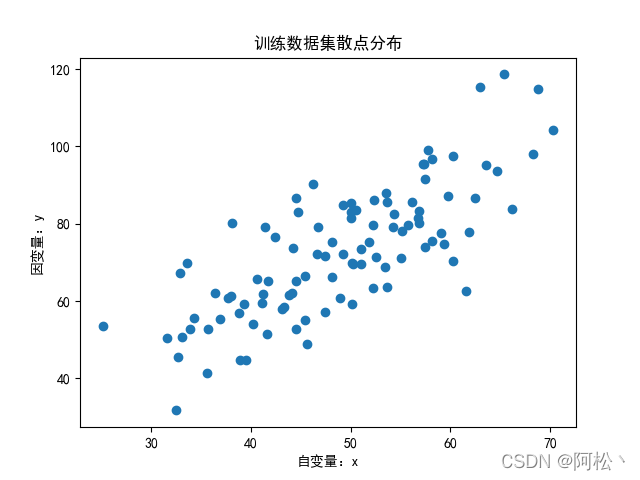
训练拟合结果:
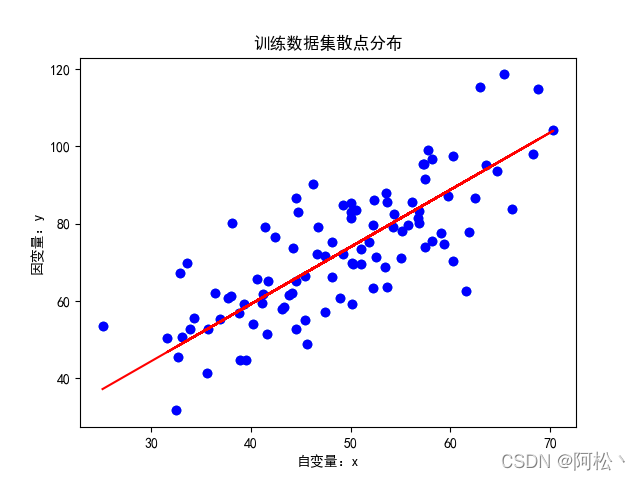

--学习笔记(下)...)


 与 经纬度(单位:弧度/度) 之间的转换。...)
![200行代码,7个对象——让你了解ASP.NET Core框架的本质[3.x版]](http://pic.xiahunao.cn/200行代码,7个对象——让你了解ASP.NET Core框架的本质[3.x版])
)
)
-区间dp)










