题目背景
上元节的庙会上，牛宝靠自己的聪明才智成功破解了花灯阵，点亮了在场所有花灯，但他没料到的是这个游戏包含AB两个项目，A项目就是点亮所有花灯，而B项目则是熄灭所有花灯。不过点亮的是花灯阵，熄灭的则是花灯环。
题目描述
熄灭花灯环的规则如下：
在一个环形的花灯圈中，每隔一段距离摆放着一个花灯堆，每个花灯堆都由一定数量的花灯组成，共有n个花灯堆(n<= 100)，现要将花灯全部熄灭，需要消耗牛宝体力值为10。不过在熄灭花灯之前，必须先将所有花灯堆聚集到一起才行。牛宝体力有限，每次只能将相邻的两个花灯堆聚集在一起,聚集成的新花灯堆的花灯数,即为牛宝消耗的体力值。
读入花灯堆数n及每堆的花灯数(<=20)。选择一种最佳聚集花灯的策略,使得所有花灯堆聚集到一起后,牛宝消耗的体力值最小,输出牛宝将花灯全部聚齐并熄灭所消耗的最少体力值。
输入格式
第一行输入一个整数n,代表环形花灯圈上有n个花灯堆
第二行输入组成每个花灯堆的花灯数
输出格式
输出一个整数，代表牛宝将花灯全部聚齐并熄灭所消耗的最少体力值
输入输出样例
输入
4
4 4 5 9
输出
53
说明/提示
牛宝正在愁思记录着搬运花灯堆所要耗费的体力。。。
话说第一次写这题的时候，还不知道区间dp这东西，我居然用循环链表模拟一个环，结果只能过一个数据点。(还是太年轻了)
循环链表模拟环
代码如下：
#include <iostream>
using namespace std;
const int N = 110;struct huan {int w;int l;int r;
};
huan node[N];
int ans;int main() {int n;int cnt;cin >> n;cnt = n;for (int i = 1; i <= n; i++) {int x;cin >> x;node[i].w = x;node[i].l = i + 1;node[i].r = i - 1;}node[0].l = 1;node[0].r = n;node[1].r = 0;node[n].l = 0;node[0].w = 999999;int u;while (cnt != 1) {bool flag = 0;int minv = 99999999;for (int i = node[0].l; i; i = node[i].l) {if ((node[i].w + node[node[i].l].w) < minv && node[i].l != 0) {u = i;minv = (node[i].w + node[node[i].l].w);} else if ((node[i].w + node[node[0].l].w < minv ) && node[i].l == 0) {u = i;flag = 1;minv = (node[i].w + node[node[0].l].w);}}ans += minv;if (flag) {node[u].w += node[node[0].l].w;node[0].l = node[node[0].l].l;node[node[0].l].r = 0;cnt--;} else {node[node[u].l].w += node[u].w;node[node[u].r].l = node[u].l;node[node[u].l].r = node[u].r;cnt--;}}cout << ans + 10 << endl;return 0;
}
原因就是，假如有很多花灯堆，刚好这边有2个花堆和那边的2个花堆合在一起所需的体力值一样且都是最小值的时候，应该合哪边的呢？？？
模拟环的方式无法处理这种情况，当然应该是我水平太低。
然后用区间dp来写，就可以解决这种情况。
解题思路：
写这道题前，先看看石子合并-区间dp这道简单一点的
这道题与石子合并-区间dp的区别是：这道题变成了环形的，处理方式是将之前的直线石子合并 ，将前n堆石子复制到n+1到2n，变成一个2n长的直线石子合并问题
，输出的时候枚举dp[i][n+i-1]，找最小值。
举个例子：
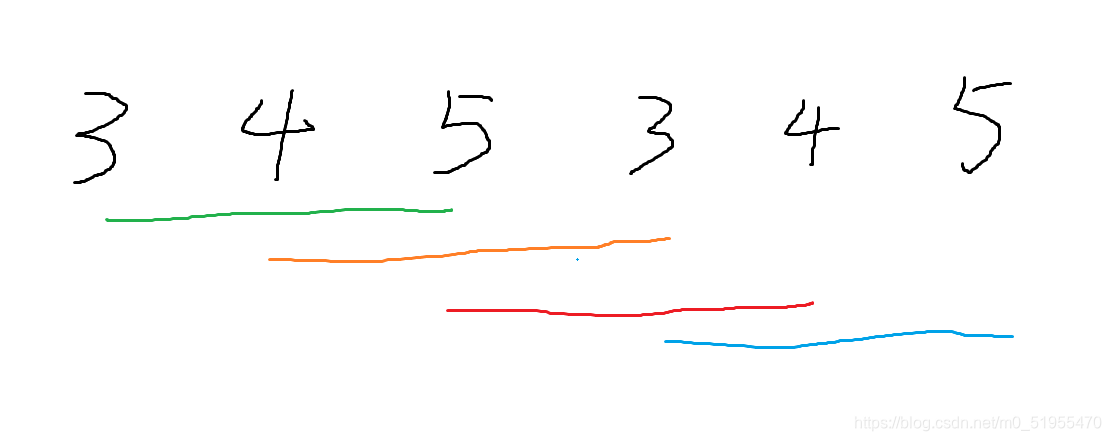可以看到，原本假如石子是3堆，为3,4,5
那么变成环形的话，我们就变成3,4,5,3,4,5
然后处理方式还是一样，只是最后我们输出的结果是长度为3情况(dp[i][n+i-1])中最小值。
代码如下：
#include <iostream>
using namespace std;
const int N = 101;
const int INF = 1 << 30;
int a[N * 2];
int s[N * 2];
int dp[2 * N][2 * N];
int n;int ans() {for (int i = 1; i <= 2 * n; i++)dp[i][i] = 0;for (int len = 1; len < 2 * n; len++)for (int i = 1; i <= 2 * n - len; i++) {int j = i + len;dp[i][j] = INF;for (int k = i; k < j; k++) {dp[i][j] = min(dp[i][j], dp[i][k] + dp[k + 1][j] + s[j] - s[i - 1]);}}int minv = 1 << 30;for (int i = 1; n + i - 1 <= 2 * n; i++) {minv = min(dp[i][n + i - 1], minv);}return minv;
}int main() {cin >> n;for (int i = 1; i <= n; i++)cin >> a[i];for (int i = n + 1; i <= 2 * n; i++)a[i] = a[i - n];s[0] = 0;for (int i = 1; i <= 2 * n; i++) {s[i] = s[i - 1] + a[i];}cout << ans()+10 << endl;return 0;
}
)
