逻辑回归
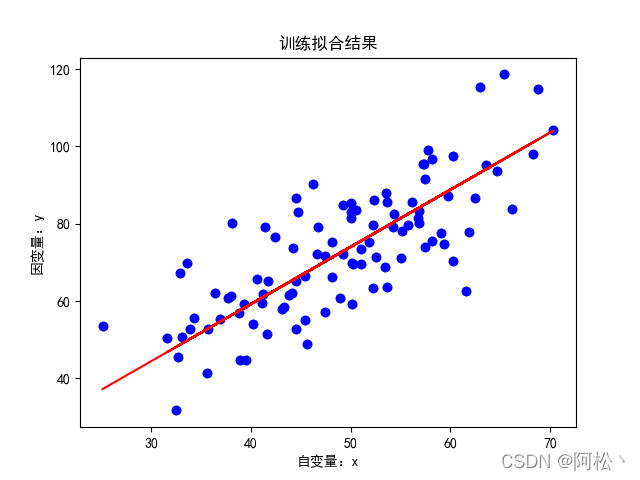
在学习逻辑回归之前我们先回顾一下线性回归。线性回归解决的是回归问题,简单来说就是,我们需要找到一个函数,这个函数需要尽可能的拟合所有训练集的样本点。
逻辑回归解决的是分类问题,它的目标是找到一个函数,利用这个函数尽可能把不同种类的数据区分开来。利用sigmod激活函数可以将前面类似线性回归的计算结果映射为离散值。
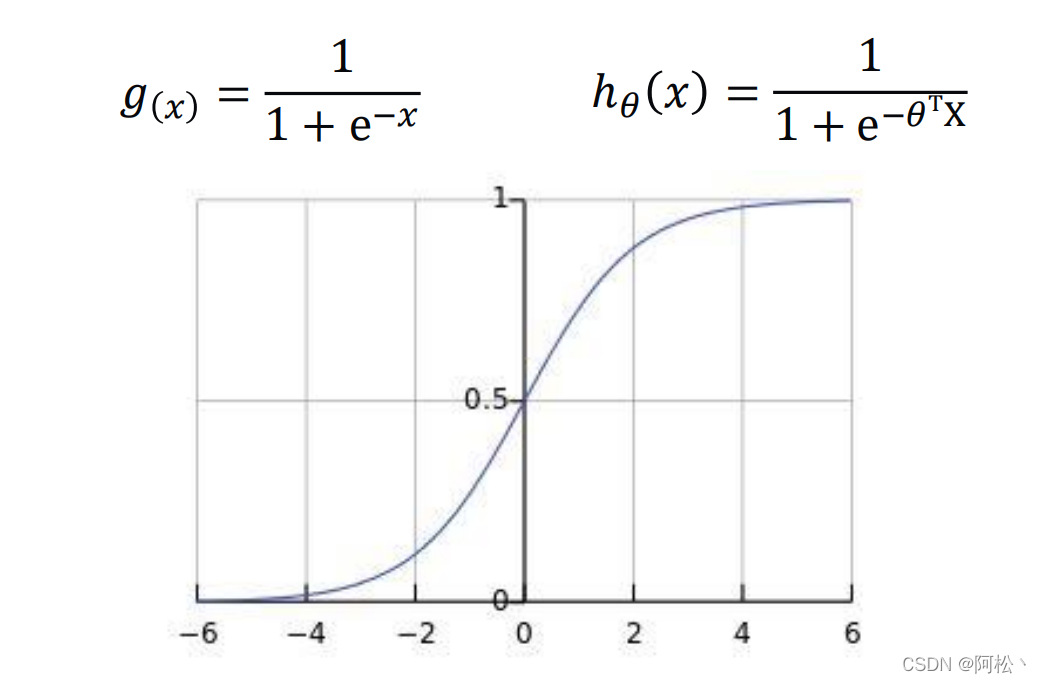
通过激活函数我们可以将下面图片中不同位置的点映射为不同的离散值。
需要注意:这个图横纵坐标都是自变量X,跟上面的线性回归是有区别的。

import matplotlib.pyplot as plt
import numpy as np
from sklearn.metrics import classification_report
from sklearn import preprocessing
# 数据是否需要标准化
scale = False# 画图正常显示中文
plt.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False # 用来正常显示负号def sigmoid(x):return 1.0 / (1 + np.exp(-x))def cost(xMat, yMat, ws):left = np.multiply(yMat, np.log(sigmoid(xMat * ws)))right = np.multiply(1 - yMat, np.log(1 - sigmoid(xMat * ws)))return np.sum(left + right) / -(len(xMat))def gradAscent(xArr, yArr):if scale == True:xArr = preprocessing.scale(xArr)xMat = np.mat(xArr)yMat = np.mat(yArr)# 学习率lr = 0.001# 迭代次数epochs = 10000# 申明一个列表用来存储losscostList = []# 计算数据行列数# 行代表数据个数,列代表权值个数m, n = np.shape(xMat)# 初始化权值ws = np.mat(np.ones((n, 1)))for i in range(epochs + 1):# xMat和weights矩阵相乘h = sigmoid(xMat * ws)# 计算误差ws_grad = xMat.T * (h - yMat) / mws = ws - lr * ws_gradif i % 50 == 0:costList.append(cost(xMat, yMat, ws))return ws, costListdef plot(x_data, y_data):x0 = []x1 = []y0 = []y1 = []# 切分不同类别的数据for i in range(len(x_data)):if y_data[i] == 0:x0.append(x_data[i, 0])y0.append(x_data[i, 1])else:x1.append(x_data[i, 0])y1.append(x_data[i, 1])# 画图scatter0 = plt.scatter(x0, y0, c='b', marker='o')scatter1 = plt.scatter(x1, y1, c='r', marker='x')# 画图例plt.title("训练数据集散点分布")plt.xlabel("自变量:x0")plt.ylabel("自变量:x1")plt.legend(handles=[scatter0, scatter1], labels=['label0', 'label1'], loc='best')plt.savefig("LR_scatter.png")# plt.show()def plot_result(ws,x_data,y_data):# 画图决策边界plot(x_data,y_data)x_test = [[-4],[3]]y_test = (-ws[0] - x_test*ws[1])/ws[2]plt.plot(x_test, y_test, 'k')plt.savefig("LR_result.png")plt.show()def plot_loss(costList):# 画图 loss值的变化x = np.linspace(0, 10000, 201)plt.plot(x, costList, c='r')plt.title('Train')plt.xlabel('Epochs')plt.ylabel('Cost')plt.savefig("LR_Loss.png")plt.show()# 预测
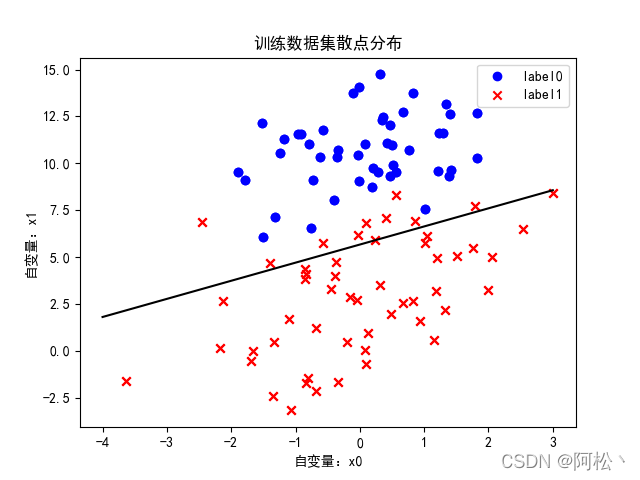
def predict(x_data, ws):if scale == True:x_data = preprocessing.scale(x_data)xMat = np.mat(x_data)ws = np.mat(ws)return [1 if x >= 0.5 else 0 for x in sigmoid(xMat*ws)]def train():# 载入数据data = np.genfromtxt("LR-testSet.csv", delimiter=",")x_data = data[:, :-1]y_data = data[:, -1]# 绘制散点图plot(x_data, y_data)# 数据处理,添加偏置项x_data = data[:, :-1]y_data = data[:, -1, np.newaxis]print("x_data的数据形状为:", np.mat(x_data).shape)print("y_data的数据形状为:", np.mat(y_data).shape)# 给样本添加偏置项X_data = np.concatenate((np.ones((100, 1)), x_data), axis=1)print("x_data添加偏执后X_data的数据形状为:", X_data.shape)# 训练模型,得到权值和cost值的变化ws, costList = gradAscent(X_data, y_data)print("训练后得到的权值列表为:", ws)print("保存决策边界结果图像")plot_result(ws, x_data, y_data)predictions = predict(X_data, ws)print(classification_report(y_data, predictions))print("保存loss下降结果……")plot_loss(costList)if __name__ == '__main__':train()运行结果:
x_data的数据形状为: (100, 2)
y_data的数据形状为: (100, 1)
x_data添加偏执后X_data的数据形状为: (100, 3)
训练后得到的权值列表为: [[ 2.05836354]
[ 0.3510579 ]
[-0.36341304]]
保存决策边界结果图像
precision recall f1-score support
0.0 0.82 1.00 0.90 471.0 1.00 0.81 0.90 53accuracy 0.90 100
macro avg 0.91 0.91 0.90 100
weighted avg 0.92 0.90 0.90 100
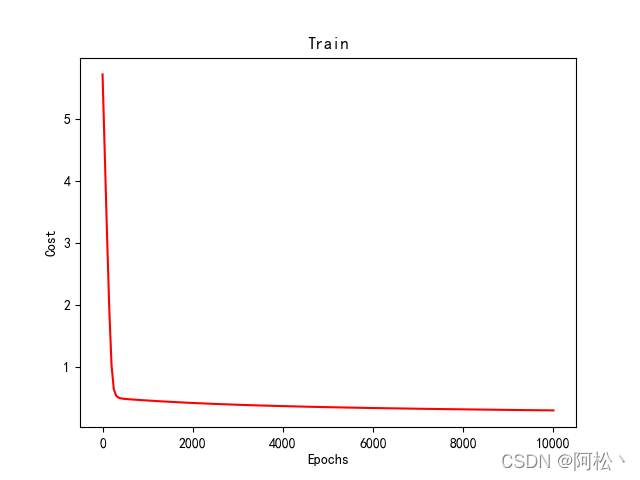
保存loss下降结果……
输出图片:
)
-区间dp)













tensorflow笔记:Tensor数据类型)

)

)