数据结构与算法--数组中的逆序对

题目：在数组中的两个数字如果签名一个数字大于后面的数组，则这两个数字组成一个逆序对。输入一个数组，求出这个数组中的逆序对的总数。
案例：输入数组{7,5，6,4}中一共有5个逆序对分别是{7,6}，{7,5}，{7,4}，{6,4}，{5,4}
如上题描述，最简单的方案就是双循环遍历整个数组，扫描第一个数字的时候让他与其他数字逐个比较，记录下比他小的数字并且累加一，这个类似冒泡排序的一个算法
双循环的方案时间复杂度与冒泡排序是一样的都是O(n²)，应该有更快的方案
方案二：
- 还是用{7,5，6,4}作为案例分析，既然我们不能拿到第一个后与后面列表逐个比较，那么我们拆解开看能否得到更优方案
- 我们将数组按从左到右拆解成一个元素一个元素的单个数组
- 接着一遍合并相邻的子数组，一遍统计逆序对的数目
- 我们用如下图解
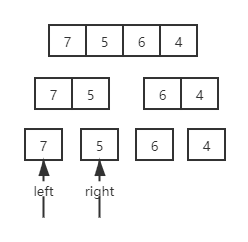
第一步，我们将数组每次拆解一半，知道数组只剩下1 个或者2个，我们此处用最好理解的方案，拆解成独立的一个
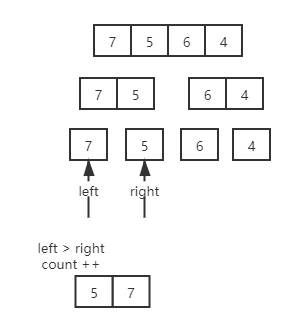
第二步，逐个比较相邻的，7 < 5 是一个逆序对，我们应该count +1，并且将两个独立数组合并成一个有序数组，同理6与4 也是一样，得到两个数组，分别是{7,5}， {6,4}
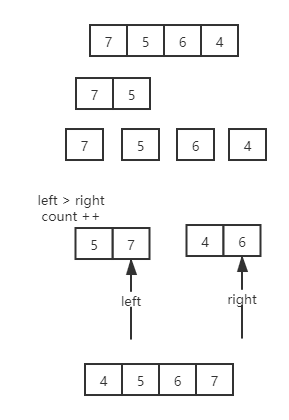
第三部接着合并得到的两个数组，并统计，如下图中，当left指针指向7 ，right指向6 此时left > right,
因为此时两个数组都是顺序的，那么left指向的数据比第二个数组中所有数都要大
那么count叠加次数应该是第二个数组的长度，或者说是right指向的数据的下标大小+1
接着移动left，right，并且将较大的数放入合并的数组中
如上步骤和我们先进行拆解，然后对子数组逐个进行统计排序的方式和我们之前文章：数据结构与算法–排序算法总结（动图演示）讲到的归并排序的思想是一样的
只不过我们之前的实现中归并排序拆解的时候选择的是拆解成2 个，因为这样可减少递归的次数
此时我们选择拆解成1个，是因为我们目的是需要统计次数，如果拆解成2个，必须在对这两个进行单独排序的时候单独统计，这样多了多余的逻辑
经如上分析有如下代码：

/*** 找出数组中所有逆序对 例如：* {7,5,6,4} => 75,76,74,54,64* @author liaojiamin* @Date:Created in 14:50 2021/6/11*/
public class InversePairs {public static Integer countInverse = 0;public static Integer[]  mergeSortFindPairs(Integer[] array){if(array == null || array.length <= 1){return array;}if(array.length < 2){return array;}Integer middle = array.length/2;Integer[] left = Arrays.copyOfRange(array, 0, middle);Integer[] right = Arrays.copyOfRange(array, middle, array.length);return merge(mergeSortFindPairs(left), mergeSortFindPairs(right));}public static Integer[] merge(Integer[] left, Integer[] right){Integer[] mergeArray = new Integer[left.length + right.length];Integer targetPosition = mergeArray.length-1;Integer leftPosition = left.length -1;Integer rightPosition = right.length -1;while (targetPosition >= 0){if(leftPosition >=0 && rightPosition >= 0){if(left[leftPosition] > right[rightPosition]){countInverse+=(rightPosition+1);mergeArray[targetPosition--] = left[leftPosition--];}else {mergeArray[targetPosition--] = right[rightPosition--];}}else {if(leftPosition < 0){while (rightPosition >= 0){mergeArray[targetPosition--] = right[rightPosition--];}}else {while (leftPosition >= 0){mergeArray[targetPosition--] = left[leftPosition--];}}}}return mergeArray;}public static void main(String[] args) {Integer[] array = {1,3,44,22,31,4,0,32,14,16,32,9,4,7,23,555,12,123,456};array = mergeSortFindPairs(array);for (int i = 0; i < array.length; i++) {System.out.println(array[i]);}System.out.println(countInverse);}
}