数据结构与算法--二叉堆（最大堆，最小堆）实现及原理

二叉堆（最大堆，最小堆）实现及原理

二叉堆与二叉查找树一样，堆也有两个性质，即结构性质和堆性质。和AVL树一样，对堆的一次操作必须到堆的所有性质都被满足才能终止，也就是我们每次对堆的操作都必须对堆中的数据进行校正才能终止。

结构性质

堆是一颗被填满的二叉树，除了最底层上的元素是不满的，但是最底层元素必须是从左到右填入。这样的树称为完全二叉树（complete binary tree），如下就是一个二叉堆的案例：
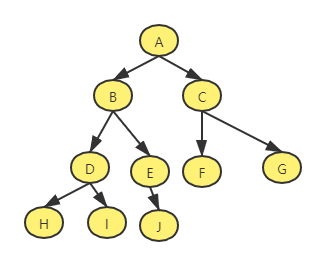
容易得到的一个层级与节点数的一个结论是，如果有一棵高度 h 的完全二叉树，节点数在2^h 到 2^h+1 - 1 个节点。这意味着完全二叉树的高是LogN，
根据观察发现重要点：因为完全二叉树是那么有规律，所有他甚至可以用一个数组来标识而不需要用连去链接，如下图中的数组来表示上图中的完全二叉树

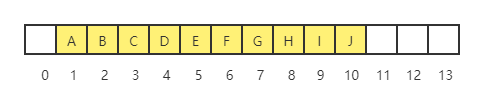
在这里插入图片描述

如上图，对于数组中任意位置 i 上的元素，其做儿子在 2*i 位置上，右儿子在左二子后的单元（2i+1）中
那么同理他的父节点就在他 i/2上，因此这里不仅不需要指针联合，而且遍历改树需要的操作也会非常简单，大部分计算机上运行可以非常快。
这种实现方法的唯一问题在于，最大的堆大小需要预先估计，也就如果我们需要存储10 个节点数据，那么数组的大小不是10 ，而需要更大的空间，这个具体值需要计算得。
如上图中堆的大小是13个元素。改数组位置 0 是没有存放数据，后面我们会详细说明实现。
因此一个堆的结构应该由一个 Comparable 对象（应为需要比较各个节点大小）数组，和一个代表当前堆大小的整数组成。

堆性质

让操作快速执行的性质是堆序性质（heap-order property）。由于我们需要快速找出最小单元，因此最小单元应该在根节点上，如果我们考虑任意子树也应该是一个堆，那么任意节点都应该小于他的子树。
应用这个逻辑，我们得到堆序性质。在一个堆中，对于每个节点X，X的父节点中关键字小于或者等于X中的关键字，根节点除外（根节点没有父节点）。如下图就是一个最小堆的示范：

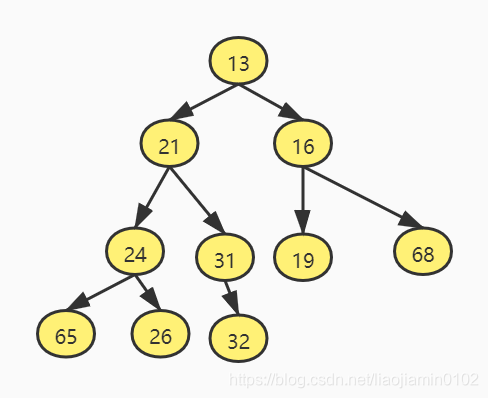
在这里插入图片描述

根据堆序性质，最小元素数据总可以在根节点处找到，也就是我们可以用O(1)时间的方法findMin。

基本的堆操作

最重要的一点在于，所有操作都必须保证堆序性质。

insert 插入操作

为了将一个元素X插入到堆中，我们可以在下一个可用位置模拟一个空的元素位置，他必须填补在此处，要不然不满足结构性质，如下图：
如上图，如果插入的数据能满足堆序性质，那么插入结束
如果插入的元素比其父节点31 要小，我们必须将空元素的父节点上的元素31 移动到空元素位置。
这样空元素位置就朝根节点的方向上移动了一个位置，继续改过程直到插入的数据X能翻入空位置为止。
例如我们需要插入的数据是 14，如下图
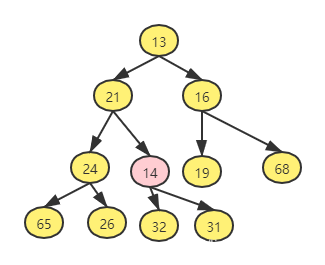
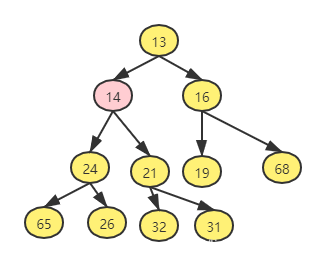
这种方法的策略上叫上滤。新元素在堆中上滤直到找出正确的位置。
如果插入的元素是新堆中最小元素，那么新元素会一直上滤到根节点出，这种插入的时间长达O(logN)，平均来看，上滤终止的要早与交换对比来看，例如我们也可以在insert中用交换来实现上滤古村，但是一次交换需要3条赋值语句。如果一个元素上滤d层，需要3d次交换，而用数组，我们先用0 保存需要插入的元素，每次只需要将应该去的位置的数据给空穴位置就行，这样只需要用d + 1 次赋值即可。

deleteMin删除最小数据

deleteMin以类似的方式处理。找出最小元素是简单的。困难地方在于怎么删除他。当删除根节点时候，相当于在根处有一个空元素。由于对堆少了一个跟元素，因此我们将堆中最后一个元素X放入根节点中。如果X比他的子节点都小，满足堆序性质，那么删除完成
如果X比他子节点大，那么找出子节点中最小者，与X交换位置
持续以上步骤，直到X找到他的位置为止。
如下案例，我们删除最小值13的流程：

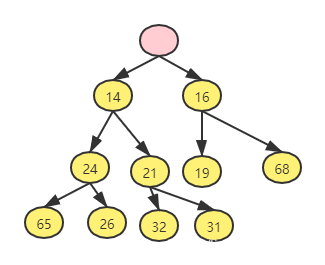
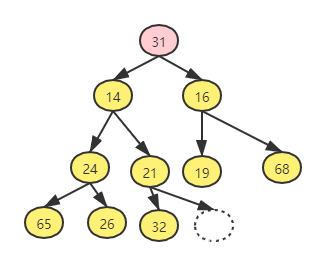
在这里插入图片描述

纠错，此处应该是与21 交换，图片有误

在这里插入图片描述

以上方式我们将堆中最后一个元素X掏出来，放入临时变量，删除min后，根变成了空元素位置
此时我们将子节点与掏出的元素X比较，如果X大于子节点，那么将子节点中最小元素放入空元素位置中，
如果X小于子节点，那么将X放入当前位置
这种策略叫下滤
实现过程中可能最后一个节点只有一个节点，我们默认的处理方式都认为有两个子节点，此处应该在比较适合判空操作。
删除操作最坏情况时间也是O(logN)，平均而言，被放到根处的元素几乎下滤到底层，因此平均运行时间也是O(logN）

代码实现

二叉堆节点定义与之前二叉树的有一点点不一样，更简单，无需指针如下代码实现：

/*** @author liaojiamin* @Date:Created in 15:57 2020/12/24*/
public class AnyType implements Comparable<AnyType> {private Object element;public AnyType(Object element){this.element = element;}public Object getElement() {return element;}public void setElement(Object element) {this.element = element;}@Overridepublic int compareTo(AnyType o) {if (o == null) {return -1;}int flag;if (o instanceof AnyType) {int myElement = Integer.valueOf(this.element.toString()) - Integer.valueOf(o.getElement().toString());flag = myElement > 0 ? 1 : myElement == 0 ? 0 : -1;} else {flag = this.element.toString().compareTo(o.toString());}if (flag == 0) {return 0;} else if (flag > 0) {return 1;} else {return -1;}}
}

具体二叉堆代码实现


/*** 二叉堆，父节点总小于子节点（最小堆），用数组实现* @author liaojiamin* @Date:Created in 15:45 2020/12/24*/
public class BinaryHeap {private static final int DEFAULT_CAPACITY = 10;/*** 当前最后一个数据下标* */private int currentSize;private AnyType[] array;public BinaryHeap(){}public BinaryHeap(int capacity){currentSize = 0;array = new AnyType[capacity];}public BinaryHeap(AnyType[] item){currentSize = item.length;array = new AnyType[(currentSize + 2 )*11/10];int i =1;for (AnyType anyType : item) {array[i++] = anyType;}buildHeap();}public void buildHeap(){for (int i = currentSize/2; i > 0; i--){percoateDown(i);}}/*** 二叉堆中添加节点（上滤方法）* */public void insert(AnyType x){if(currentSize == array.length){enlargArray(currentSize*2+1);}int hole = ++currentSize;for(array[0] = x; x.compareTo(array[hole/2]) < 0;hole = hole/2){array[hole] = array[hole/2];}array[hole] = x;}/*** 查找最小值，二叉堆最小值是根节点* */public AnyType findMin(){return array[1];}/*** 删除最小值（根节点）* */public AnyType deleteMin(){if(isEmpty()){return null;}AnyType min = findMin();array[1] = array[currentSize--];array[currentSize + 1] = null;percoateDown(1);return min;}/*** 判断是否为空* */public boolean isEmpty(){if(array == null || array.length <= 0 || currentSize == 0){return true;}for (AnyType anyType : array) {if(anyType != null){return false;}}return true;}/*** 置空整个二叉堆* */public void makeEmpty(){array = new AnyType[DEFAULT_CAPACITY];}/*** 将顶部较大的节点逐步下滤* */public void percoateDown(int hole){int child=0;AnyType tem = array[hole];for (;hole*2<=currentSize;hole=child){child = 2*hole;if(child<=currentSize && array[child].compareTo(array[child+1]) > 0){child ++;}if(array[child].compareTo(tem) < 0){array[hole] = array[child];}else {break;}}array[hole] = tem;}/*** 扩容* */public void enlargArray(int newSize){AnyType[] newArray = new AnyType[newSize];for (int i = 0; i < array.length; i++) {newArray[i] = array[i];}array = newArray;}public static void main(String[] args) {Integer size = 10;BinaryHeap binaryHeap = new BinaryHeap((size + 2 )*11/10);Random random = new Random();for (int i = 0; i < size; i++) {AnyType anyType = new AnyType(random.nextInt(100));binaryHeap.insert(anyType);}while (!binaryHeap.isEmpty()){System.out.println(binaryHeap.deleteMin().getElement());}}
}

以上源码我们实现的是最小堆的情况，可以将比较参数修改一下得到以下最大堆的实现代码：


/*** 二叉堆，父节点总大于子节点（最大堆），用数组实现* @author liaojiamin* @Date:Created in 15:45 2020/12/24*/
public class BinaryHeapMax {private static final int DEFAULT_CAPACITY = 10;/*** 当前最后一个数据下标* */private int currentSize;private AnyType[] array;public BinaryHeapMax(){}public BinaryHeapMax(int capacity){currentSize = 0;array = new AnyType[capacity];}public BinaryHeapMax(AnyType[] item){currentSize = item.length;array = new AnyType[(currentSize + 2 )*11/10];int i =1;for (AnyType anyType : item) {array[i++] = anyType;}buildHeap();}public AnyType[] getAppHeapData(){return Arrays.copyOfRange(array, 1, currentSize+1);}/*** 获取当前最大堆数据量* */public Integer heapSize(){return currentSize;}public void buildHeap(){for (int i = currentSize/2; i > 0; i--){percoateDown(i);}}/*** 二叉堆中添加节点（上滤方法）* */public void insert(AnyType x){if(currentSize == array.length){enlargArray(currentSize*2+1);}int hole = ++currentSize;for(array[0] = x; x.compareTo(array[hole/2]) > 0;hole = hole/2){array[hole] = array[hole/2];}array[hole] = x;}/*** 查找最小值，二叉堆最小值是根节点* */public AnyType findMax(){return array[1];}/*** 删除最小值（根节点）* */public AnyType deleteMax(){if(isEmpty()){return null;}AnyType max = findMax();array[1] = array[currentSize--];array[currentSize + 1] = null;percoateDown(1);return max;}/*** 判断是否为空* */public boolean isEmpty(){if(array == null || array.length <= 0 || currentSize == 0){return true;}for (AnyType anyType : array) {if(anyType != null){return false;}}return true;}/*** 置空整个二叉堆* */public void makeEmpty(){array = new AnyType[DEFAULT_CAPACITY];}/*** 将顶部较大的节点逐步下滤* */public void percoateDown(int hole){int child=0;AnyType tem = array[hole];for (;hole*2<=currentSize;hole=child){child = 2*hole;//此处需要添加array[child+1]，因为我们是默认每个父节点都满子节点，那么必然遇见单个子节点情况，此时我们compareTo方法对比null对象返回的-1，这个是为了方便min情况时候，可以看到min情况时候无需增加这个条件，因此此处有不同用来兼容null节点情况。if(child<=currentSize && array[child].compareTo(array[child+1]) < 0 && array[child+1] != null){child ++;}if(tem.compareTo(array[child]) < 0){array[hole] = array[child];}else {break;}}array[hole] = tem;}/*** 扩容* */public void enlargArray(int newSize){AnyType[] newArray = new AnyType[newSize];for (int i = 0; i < array.length; i++) {newArray[i] = array[i];}array = newArray;}public static void main(String[] args) {Integer size = 10;BinaryHeapMax binaryHeap = new BinaryHeapMax((size + 2 )*11/10);Random random = new Random();for (int i = 0; i < size; i++) {AnyType anyType = new AnyType(random.nextInt(100));binaryHeap.insert(anyType);}while (!binaryHeap.isEmpty()){System.out.println(binaryHeap.deleteMax().getElement());}}
}