leetcode63. 不同路径 II

一:题目

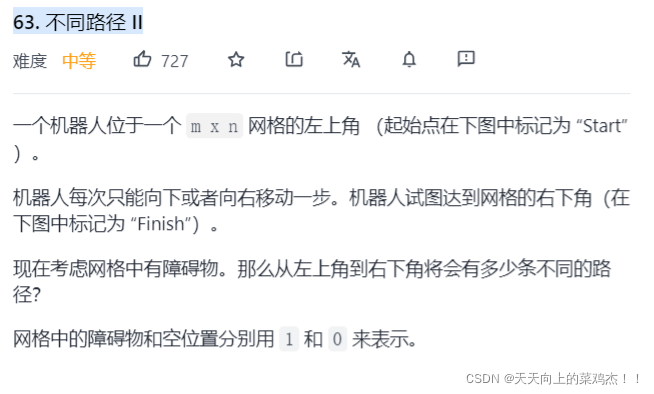
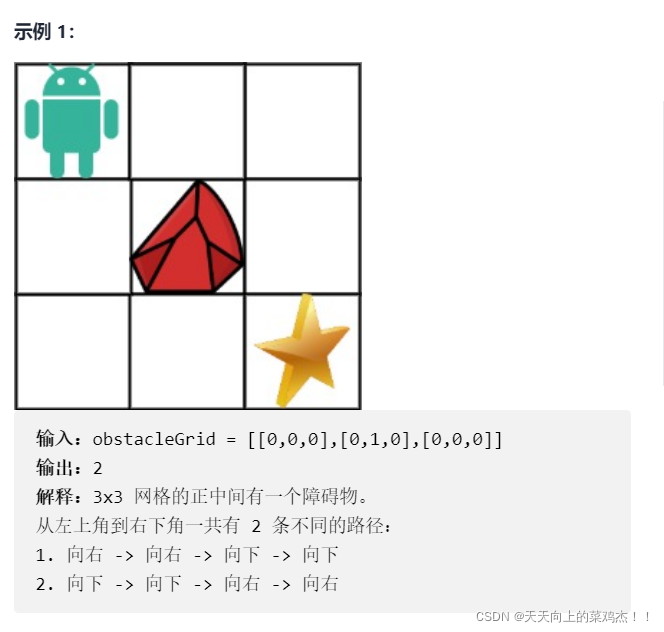
在这里插入图片描述

二：上码

class Solution {
public:/**思路:1.分析题意:这里有障碍物,所以我们的做法会有点变化，如果这个障碍物出现在左侧或则右测的话那么我们确定的是其障碍物包括其后面的下标将均为0,如果障碍物出现在上诉区域外的话，那么就直接dp[i][j] = 0;2.动态规划五步走1>:确定dp数组的含义，以及下标的含义。dp[i][j] 表示到达下标为i和j的时候,有多少路数2>:确定dp数组的递推公式到达dp[i][j]的话,只能从上方或者左方来左方:dp[i-1][j]上方:dp[i][j-1]dp[i][j] = dp[i-1][j] + dp[i][j-1];3>:确定dp数组的初始化这里的上侧和左侧;如果没障碍物的话 那么就为1，有障碍物的下标为0,其后面也将为04>:确定dp数组的遍历顺序从左向右5>:举例验证obstacleGrid = [[0,0,1,0],[0,0,0,0],[0,0,0,0]]0  1  0  01  2  2  21  3  5  7*/int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {//cout << obstacleGrid.size() << endl;//这个是测试有几组数据也就是几行数据//cout << obstacleGrid[0].size() << endl;//测试每组数据中有几个元素int m = obstacleGrid.size();//行int n = obstacleGrid[0].size();//列vector<vector<int> >dp(m,vector<int>(n,0));for(int i = 0; i < n; i++) {//行不动列在变if(obstacleGrid[0][i] == 1) {//遇见障碍物break;}dp[0][i] = 1;}for(int j = 0; j < m; j++) {//列不动 行在变 这里从1开始因为第一个格不用管他if(obstacleGrid[j][0] == 1) {break;}dp[j][0] = 1;}for(int i = 1; i < m; i++) {for(int j = 1; j < n; j++) {if(obstacleGrid[i][j] == 1) {//反正dp[i][j] == 0;continue; }else{dp[i][j] = dp[i-1][j] + dp[i][j-1];}}}cout << n << m;for(int i = 0; i < n; i++) {//   for(int j = 0; j < n; j++) {cout << obstacleGrid[0][i] << ' ';cout << "wyy";// }//     cout << endl;}return dp[m-1][n-1];}
};