首先介绍一个非常著名的多分类数据集 MNIST，也就是 0 到 9 的手写数字数据集。每个图像都是 28 * 28，用于Pytorch 数据读取的格式是 NCHW，即 Number、Channel、Height、Weight。

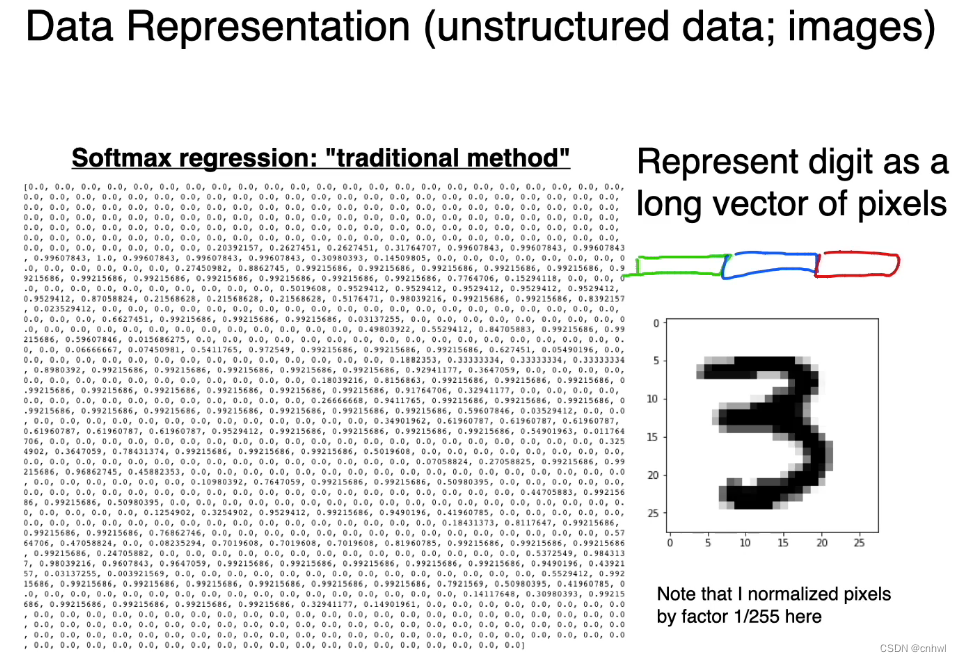
读取图像之后，就能看到一个只有单通道的（灰度）图像，实际上就是一行行像素值的组合，用于 Softmax Regression 时输入得是一个向量，所以要将一行行的像素进行拼接，成为一个长的向量。同时，将像素值从 0 - 255 转化为 0 - 1 有利于梯度下降。

回顾之前的 Logistic Regression，就是输入向量 x 与权重向量 w 做点积再加上偏置 b 得到 Net input（加权和），然后经过 Sigmoid 函数，得到一个概率输出，这个概率就是在输入为 x 的条件下预测为 y = 1 的后验概率。

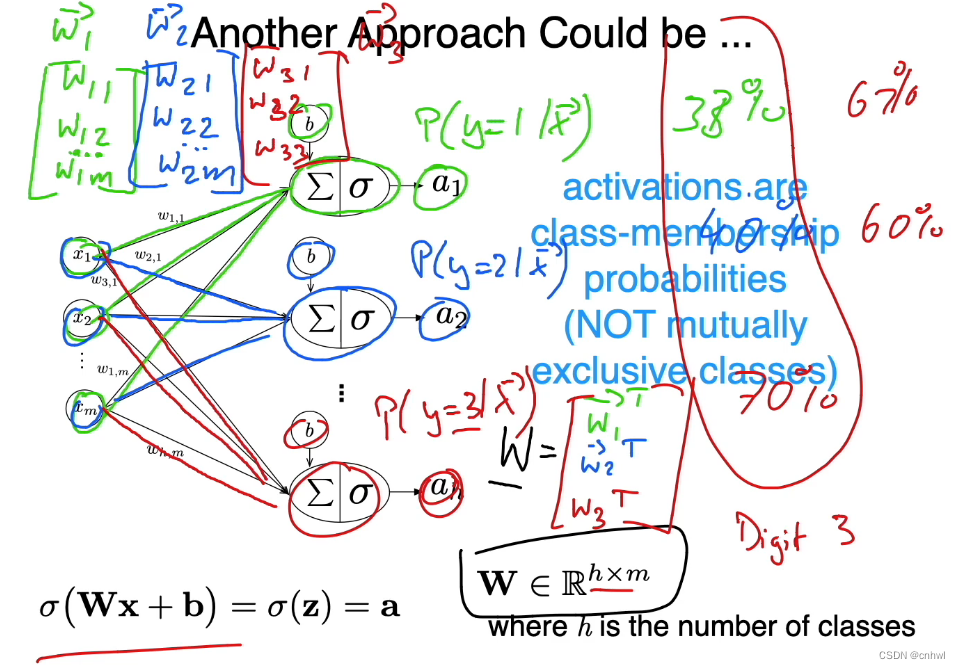
将 Logistic Regression 拓展到多分类任务中，最简单的方法就是使用多个 Logistic Regression，当类别数为 h ，输入特征数为 m 时，可以得到 h 个长度为 m 的权重向量 w，构成的权重矩阵 W 大小为 h * m。每一个概率输出都是当输入为 x 时预测为某一个类的后验概率，但是各个类的概率之和不为 1，因此该模型适用于不互斥类的多分类任务。

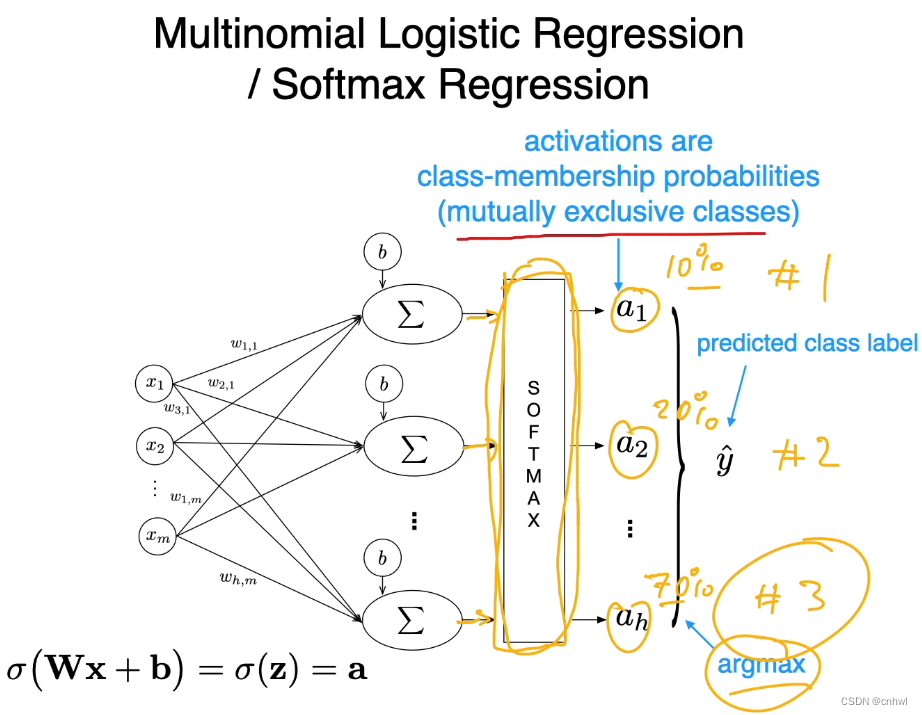
对于互斥类的多分类任务，我们希望各个类的输出概率之和为 1，此时就可以使用 Softmax 函数。

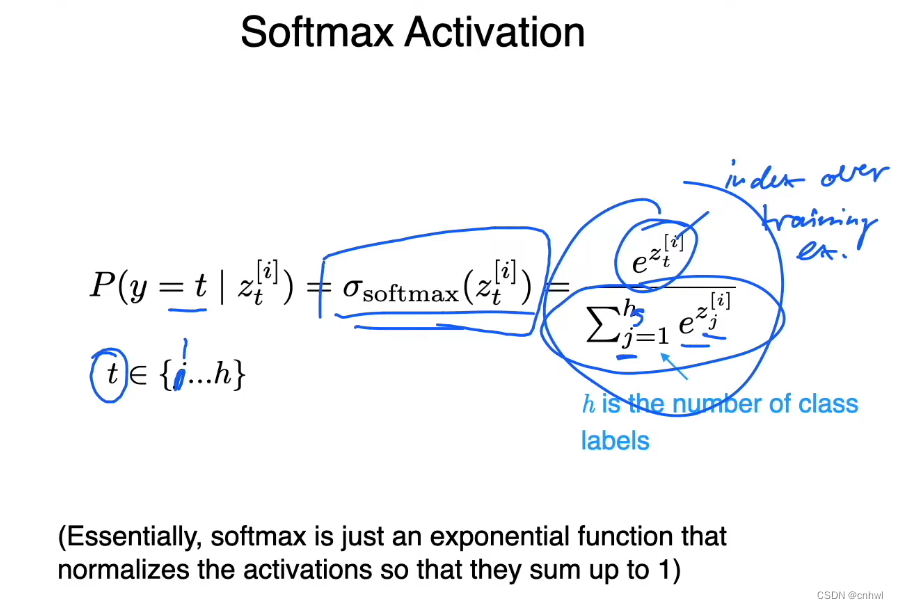
Softmax 函数实际上就是一个指数归一化函数，使得 h 个类的后验概率求和等于 1

假设有四个训练样本，它们的标签分别为 0、1、3、2，经过 Onehot Encoding 之后，就能得到四个标签向量（行向量），如第一个训练样本的标签向量为 [1, 0, 0, 0]

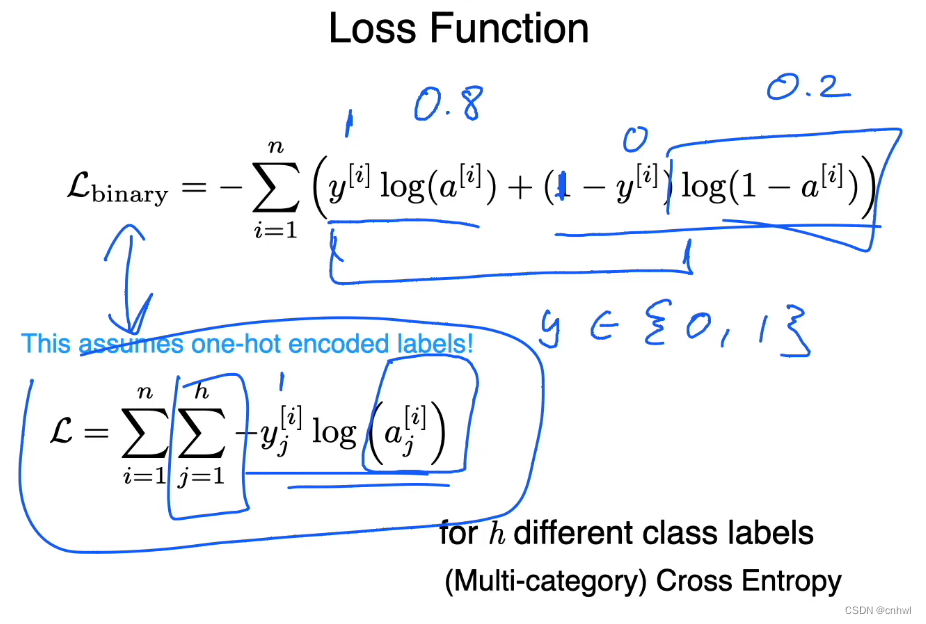
引出 Onehot Encoding 之后，就可以介绍交叉熵损失函数的拓展 —— 多元交叉熵了。$y^{[i]}$ 是第 i 个训练样本的标签向量，如前面举例过的 [1, 0, 0, 0]；${y_j}^{[i]}$ 则表示第 i 个训练样本的标签向量的第 j 个类位置的取值，也就是 0 或 1；${a_j}^{[i]}$ 则是 Softmax 函数输出矩阵的对应位置的值，即第 i 行第 j 列的值。下面是例子：

假设我们有四个训练样本，类别数为 3，则标签矩阵和 Softmax 的输出矩阵都是 4 * 3；计算第一个训练样本的 Loss，就是标签矩阵的第一行与 Softmax 输出矩阵的第一行对应位置的 log ，相乘再相加。

四个训练样本的 Loss 计算都是同理

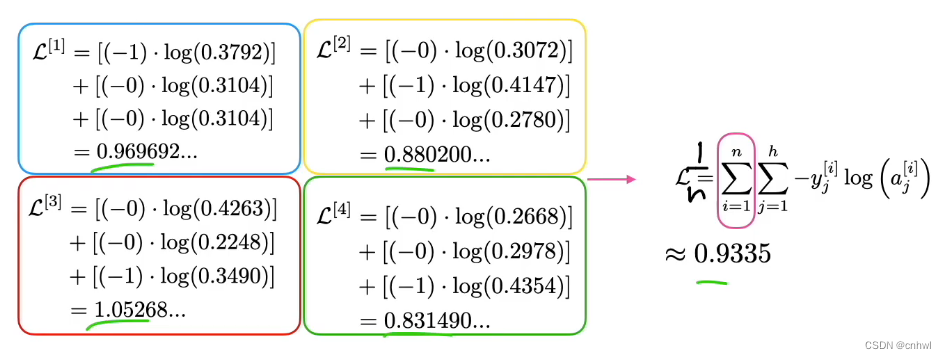
将各个训练样本的 Loss 加起来就是训练集上的损失。

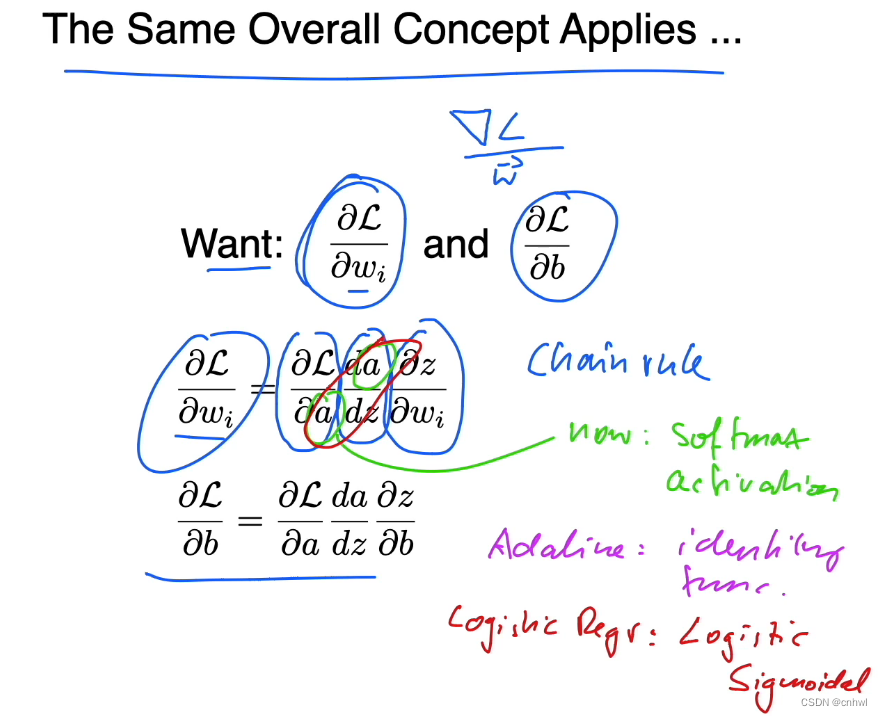
想要使用梯度下降更新参数，核心就是求得损失关于参数的偏导数，即梯度。借助链式法则，可以将损失关于参数的偏导数分解成：损失关于激活函数输出的偏导数 + 激活函数关于加权和（Net Input）的偏导数 + 加权和关于参数的偏导数

将 Softmax Regression 以图形的形式表现出来，注意这不是多层感知器，还是单层的，z1 、z2 是 Softmax 的输入，而 a1、a2 是 Softmax 的输出，中间的连线不代表权重。

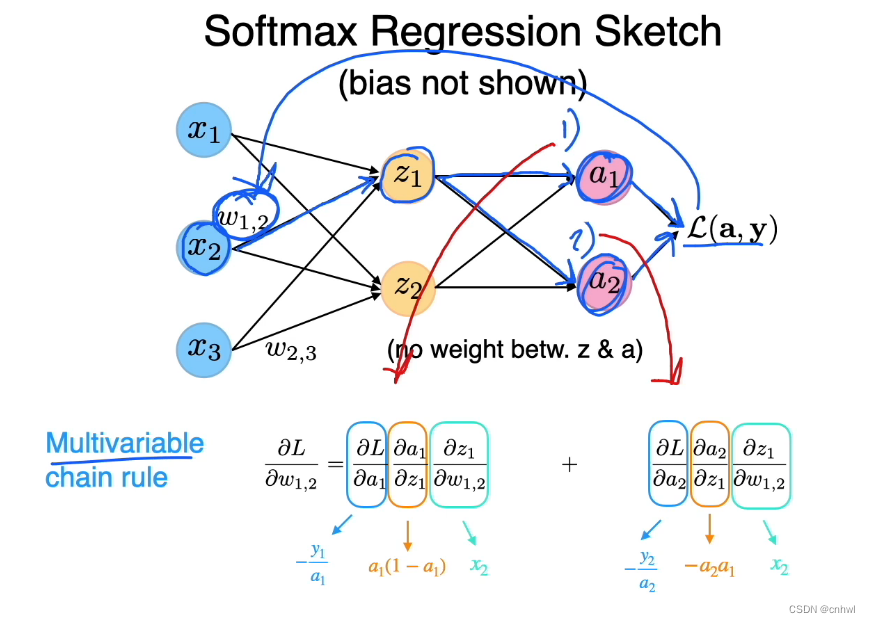
假设要求损失 $L$ 关于 $w_{1,2}$ 的偏导数，由于 $L$ 有多个输入变量 $a_1$ 和 $a_2$，所以用链式法则分解后的两部分要相加。

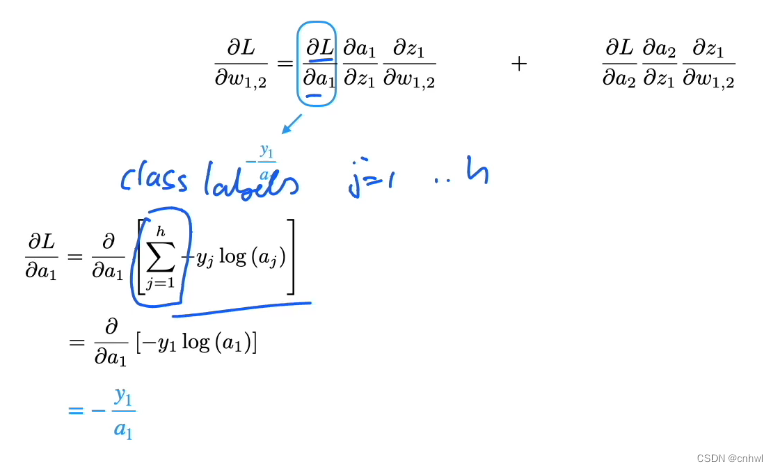
损失关于激活函数输出的偏导数，记住损失是多元交叉熵损失，对于一个激活函数输出求偏导数，如 $a_1$，则其余的 $a_2,a_3,...,a_h$ 都是常数，求导为 0

激活函数（Softmax）关于加权和的偏导数，利用的是商的求导或者除法法则，分子为 f，分母为 g，一路按照公式求解即可。

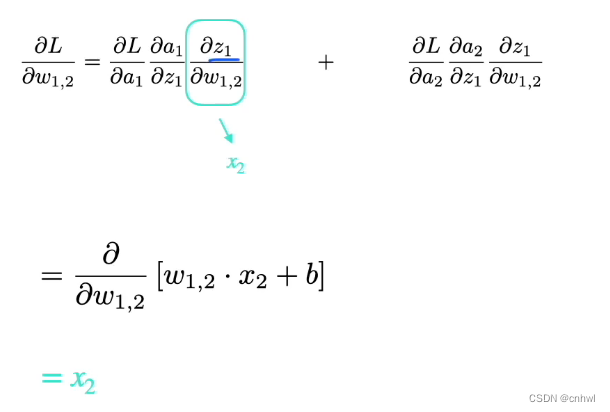
加权和关于参数的偏导数，比较简单

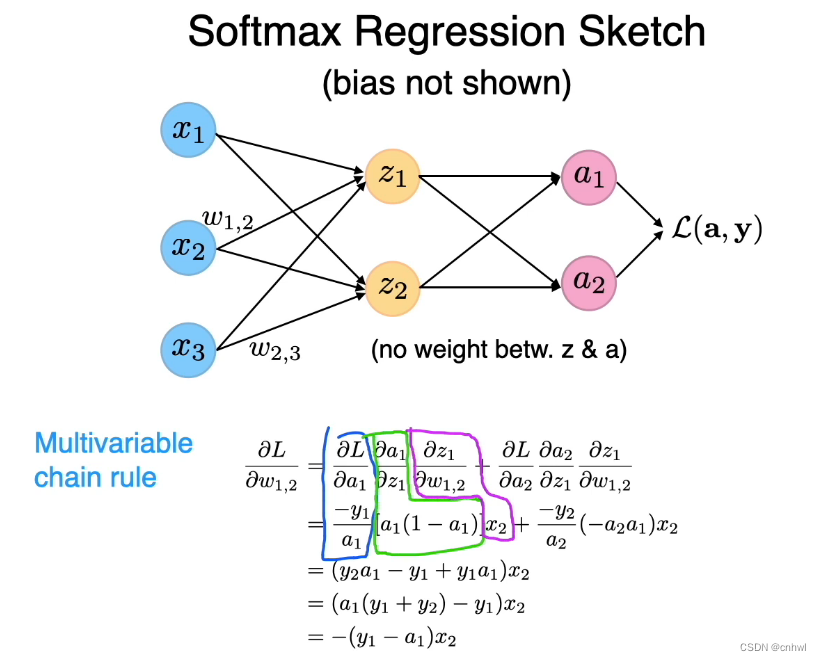
分别求出三部分的偏导数后相乘，再相加，可以得到很简洁的学习规则，实际上 Softmax Regressopm 和 Logistic Regression 的学习规则是一样的。