最优化问题通常是指对于给定的某一函数，求其在指定作用域上的全局最小值，一般情况下，最优化问题一般分为三种情况：
（1）无约束条件
对于无约束条件的优化问题中，如果一个函数 f 是凸函数，那么可以直接通过 f(x) 的梯度等于 0 来求得全局极小值点。
为了避免陷入局部最优，人们尽可能使用凸函数作为优化问题的目标函数。
凸集定义：欧式空间中，对于集合中的任意两点的连线，连线上任意一点都在集合中，我们就说这个集合是凸集。
凸函数定义：对于任意属于 [0,1] 的 a 和任意属于凸集的两点 x, y，有 f( ax + (1-a)y ) <= a * f(x) +(1-a) * f(y)，几何上的直观理解就是两点连线上某点的函数值，大于等于两点之间某点的函数值。凸函数的任一局部极小点也是全局极小点
半正定矩阵的定义：特征值大于等于 0 的实对称矩阵。
半正定矩阵的充要条件：行列式（ n 阶顺序主子式）等于 0，行列式的 i 阶顺序主子式>=0，i 从 1 到 n-1
凸函数的充要条件：如果 f(x) 在开凸集 S 上具有二阶连续偏导数，且 f(x) 的海塞矩阵（二阶偏导的矩阵）在 S 上处处半正定，则 f(x) 为 S 上的凸函数。
（2）等式约束条件
解决方法就是拉格朗日乘数法，下面就用例子引出这个方法。
假设我们想要求一个多元函数 f(x,y)=x2yf(x,y) = {x^2}yf(x,y)=x2y 的最大值，将其可视化如上图所示，是一个蓝色的类似于马鞍的曲面。但同时我们约束 x2+y2=1{x^2} + {y^2} = 1x2+y2=1，反映到函数曲面上就是红色的曲线，求 f(x,y)f(x,y)f(x,y) 的最大值也就是求红色曲线上最高的点。
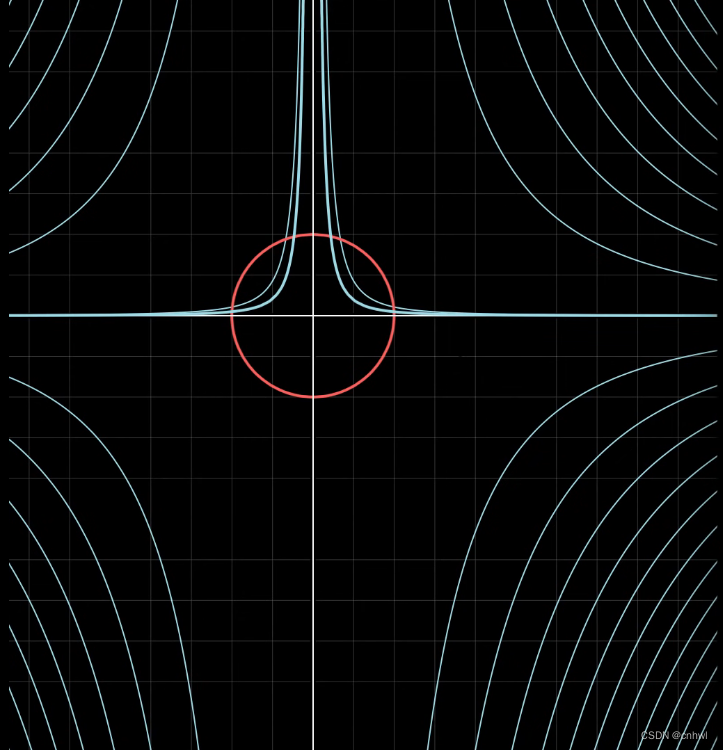
我们可以用等高线来描述函数 f(x,y)=x2yf(x,y) = {x^2}yf(x,y)=x2y，每一条等高线就是函数取同一个值的点的连线，例如下面分别为 x2y=1{x^2}y = 1x2y=1 和 x2y=0.1{x^2}y = 0.1x2y=0.1 的等高线：
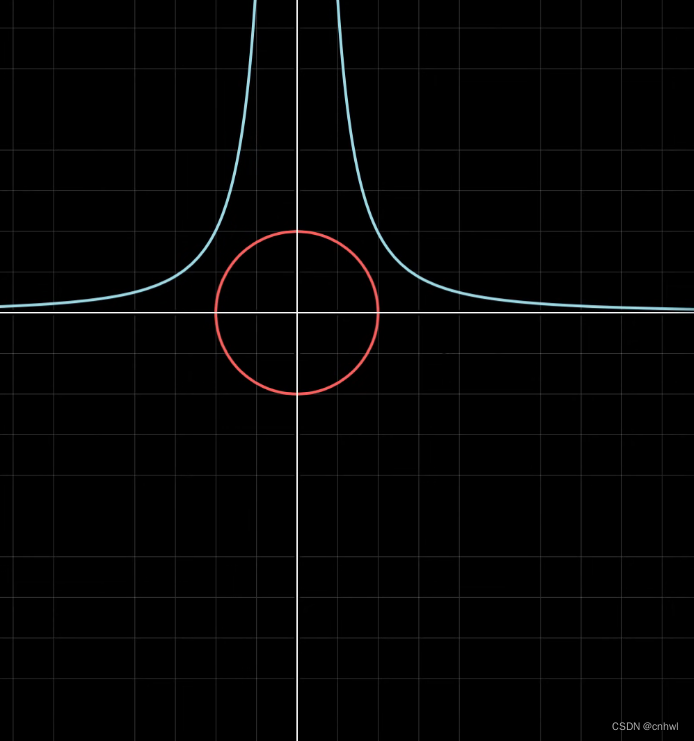
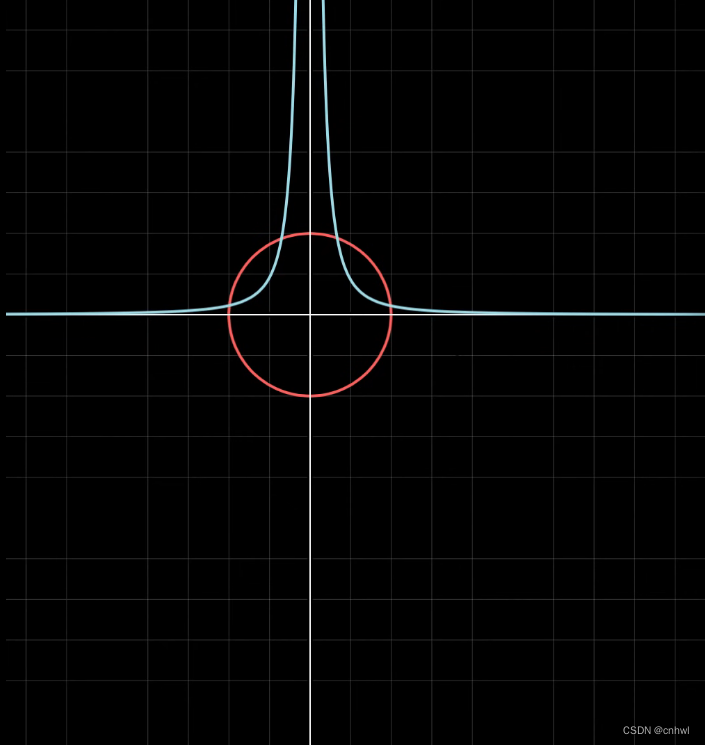
显然，x2y=1{x^2}y = 1x2y=1 与红色圆不相交，说明它不满足 x2+y2=1{x^2} + {y^2} = 1x2+y2=1 的约束条件。x2y=0.1{x^2}y = 0.1x2y=0.1 虽然与红色圆相交了，但我们希望找到最大的值，使得函数 f(x,y)=x2yf(x,y) = {x^2}yf(x,y)=x2y 与红色圆是正好相切的。我们可以把约束条件当作是函数 g(x,y)=x2+y2g(x,y) = {x^2} + {y^2}g(x,y)=x2+y2 的一条等高线，则画出两个函数 f 与 g 的等高线与梯度如下：
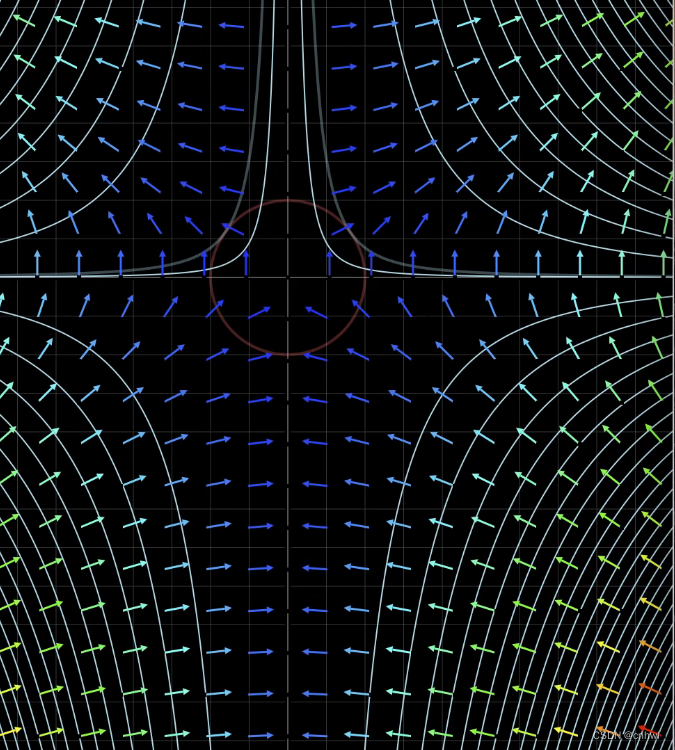
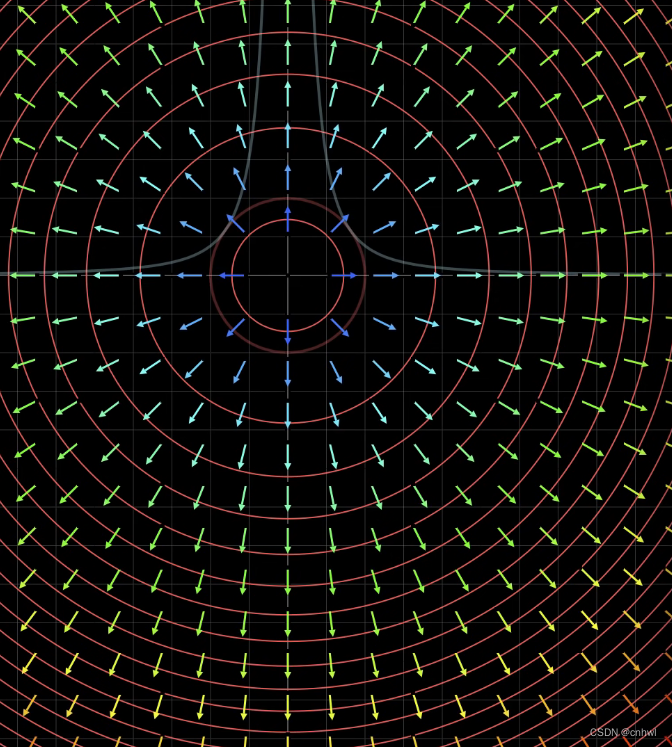
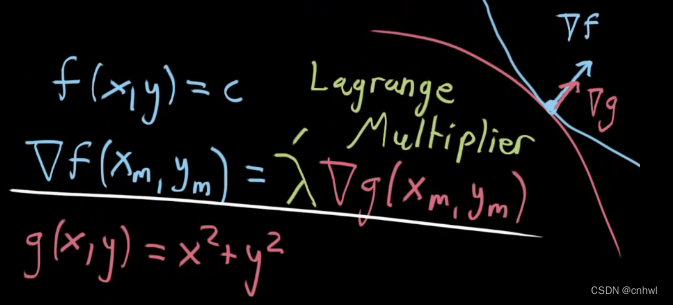
根据梯度向量的性质可知，梯度向量是垂直于等高线的，在两个函数 f 和 g 相切的位置，两者的等高线在切点处是重合的，因此 f 和 g 在切点处的梯度向量 ∇f\nabla f∇f 和 ∇g\nabla g∇g 方向相同，只有大小上的不同，两者的比值用系数 λ 表示，被称为拉格朗日乘数。
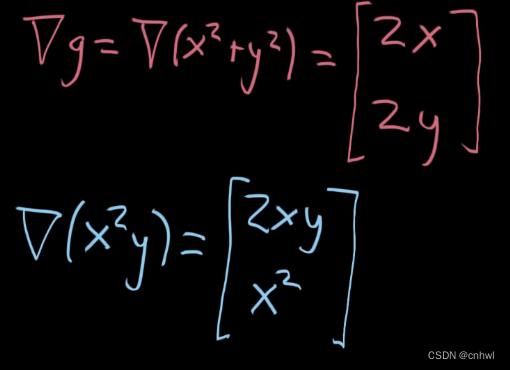
如果分别求出 f 和 g 的梯度向量 ∇f\nabla f∇f 和 ∇g\nabla g∇g，代入到 ∇f=λ∇g\nabla f = \lambda \nabla g∇f=λ∇g 中，可以得到两个方程，再加上约束条件，共三个方程，可以求解三个变量 x、y 和 λ，过程如下：
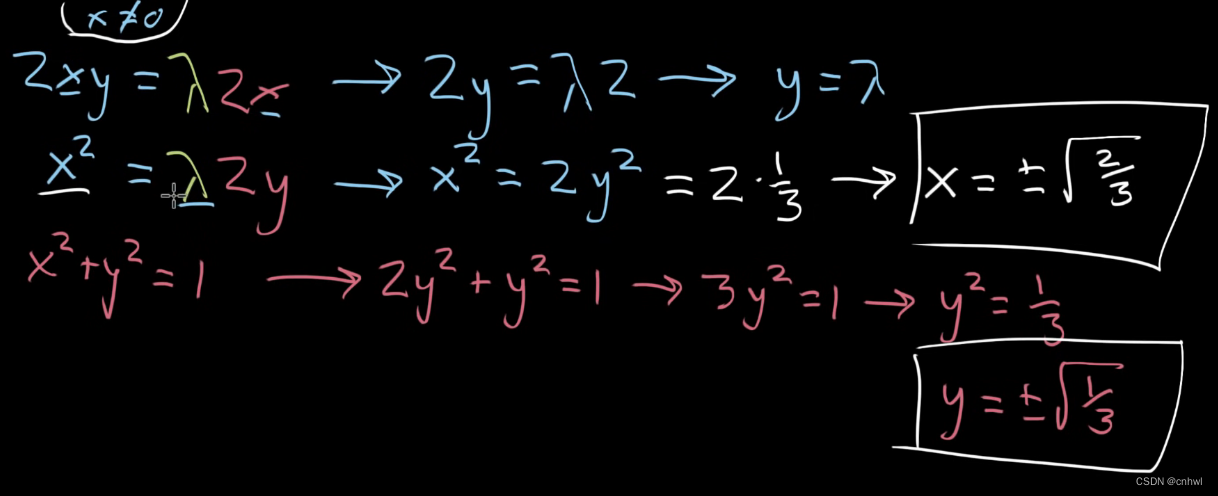
下面再引出拉格朗日函数，实际上就只是在写法上更为紧凑而已
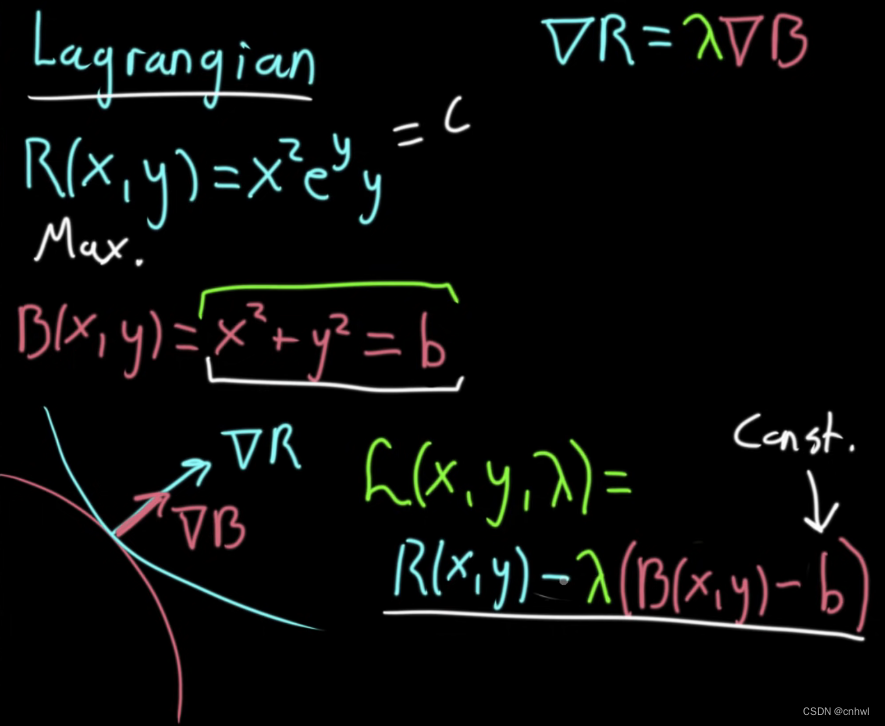
假设我们想求函数 R(x,y)=x2eyyR(x,y) = {x^2}{e^y}yR(x,y)=x2eyy 的最大值，约束条件为函数 B(x,y)=x2+y2=bB(x,y) = {x^2} + {y^2} = bB(x,y)=x2+y2=b，所谓的拉格朗日函数就是 L(x,y,λ)=R(x,y)−λ(B(x,y)−b)L(x,y,\lambda ) = R(x,y) - \lambda (B(x,y) - b)L(x,y,λ)=R(x,y)−λ(B(x,y)−b)
之所以这么做，是因为对 L(x,y,λ)L(x,y,\lambda )L(x,y,λ) 求梯度 ∇L\nabla L∇L 再令它等于 0 的话，就能得到三条方程，实际上就是基于 ∇R=λ∇B\nabla R = \lambda \nabla B∇R=λ∇B 和初始条件得到的那三条方程。
