#include<iostream>
#include<iomanip>
using namespace std;
//前i个物品装入容量为j的背包中获得的最大价值//0-1背包动态规划算法   构造二维表
int  knapsack_problem( int n,int *weight,int *value,int capacity,int **m,int *flag)
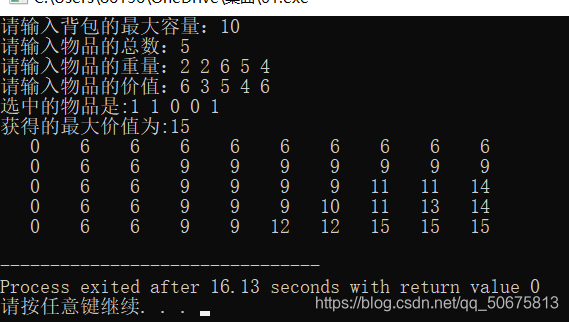
{for(int i=0;i<=capacity;i++)//赋值第一行 为0 {m[0][i]=0;// 初始化：背包容量为0时，前i个物品无法装入，获得最大价值为0}for(int i=0;i<=n;i++)//第一列赋值为0 {m[i][0]=0;//初始化：物品数量为0时，背包容量j无论多大，获得最大价值为0} for(int i=1;i<=n;i++) //构造二维表：行对应前i个物品；列对应背包容量j{for(int j=1;j<=capacity;j++){if(j<weight[i])  	//背包容量不够第i个物品的重量大{m[i][j]=m[i-1][j]; //不装，获得的最大价值仍然等于前i-1个物品装入情况的}else{	//装，看看是装入后获得的最大价值大还是前i-1个物品装入情况的最大价值大，比较后选择最大的m[i][j]=max(m[i-1][j],m[i-1][j-weight[i]]+value[i]);}}} //标记那个物品最终放到了背包里了吗 int temp_capacity=capacity;//于背包的最大容量C for(int i=n;i>0;i--)//从后往前遍历，如果装了第i个物品则标志位x[i]=1{if(m[i][temp_capacity]>m[i-1][temp_capacity])//判断第i个物品有没有装进去{flag[i]=1;	//第i个物品装了进去temp_capacity=temp_capacity-weight[i];//装了进去就将该物品的重量减去，j为剩余容量}else{flag[i]=0;//第i个物品没装进去}}cout << "选中的物品是:";for(int i=1;i<=n;i++){cout<<flag[i]<<" ";}cout<<endl;return m[n][capacity];}
int main()
{int n,capacity;cout<<"请输入背包的最大容量：";cin>>capacity;cout<<"请输入物品的总数：";cin>>n;int weight[n+1],value[n+1];cout<<"请输入物品的重量：";for(int i=1;i<=n;i++){cin>>weight[i];}cout<<"请输入物品的价值：";for(int i=1;i<=n;i++){cin>>value[i];}int **m=new int *[n+1];//开辟行 for(int i=0;i<=n;i++){m[i]=new int [capacity+1];//开辟列 }int flag[n+1];cout<< "获得的最大价值为:"<<knapsack_problem(n,weight,value,capacity,m,flag)<<endl;for(int i=1;i<=n;i++){for(int j=1;j<=capacity;j++){cout<<setw(4)<<m[i][j]<<" ";}cout<<endl;}}