
曾经有一个著名的骗局:
小明是一个赌马爱好者,最近他连续几次提前收到了预测赌马结果的邮件,从一开始由于不屑而错失良机,到渐渐深信不疑,直到最后给邮件发送方汇了巨款才发现上当。
看过这个的人应该知道,骗子收集到一份邮件信息后,分组发送不同预测结果的邮件,赌马结果公布后,再将筛选出来的那部分人分组,继续发送下一轮预测邮件。几轮过后,肯定能保证一部分人收到的预测结果是完全正确的。这也是最关键的部分。

那么骗子是如何从几万或几十万用户中寻找这些“幸运儿”的呢?这是一种二分法的思想。
假如要顺序在100万人中寻找一个人,最多需要100万次,而二分法只需要18次。
下面讲讲一些能够解决生活中一些具体问题的常用算法。
二分查找

对于一个长度为N的数组,简单查找最多需要N步;二分查找最多只需要logN步(约定底数为2)。
二分查找相较于简单查找,极大地提高了效率,但是二分查找的前提是列表是有序的,这也导致了诸多限制。
快速排序

D&C
D&C(divide and conquer)分而治之是一种重要的解决问题思路。当面对问题束手无策时,我们应该考虑一下:分而治之可以解决吗?
现在有一个问题,假如一块土地(1680*640)需要均匀地分为正方形,而且正方形的边长要尽量的大。该怎么分?
这个问题本质就是求两条边长的最大公因数。可以使用欧几里得算法(辗转相除)
快速排序
快速排序是一种常用的排序算法,比选择排序快得多(O(n^2)),快速排序也使用了D&C。
选择基准值
将数组分成两个子数组:基准值左边的数组和基准值右边的数组
对这两个数组进行快速排序
快速排序的最糟情况是O(n^2),O(n^2)已经很慢了,为什么还要叫它快速排序呢?
快速排序的平均运行时间为O(nlogn),而合并排序的时间总是O(nlogn),合并排序似乎更有优势,那为什么不用合并排序呢?
因为大O表示法中的n是一个常量,当两种算法的时间复杂度不一样时,即使n在数值上不同,对总时间的影响很小,所以通常不考虑。
但有些时候,常量的影响很大,对快速排序和合并排序就是这样,快速排序的常量小得多,所以当这两种算法的时间复杂度都为O(nlogn)时,快速排序要快得多。而相较于最糟的情况,快速排序遇上平均情况的可能性更大,所以可以稍稍忽视这个问题。(快速排序最糟的情况下调用栈为O(n),在最佳情况下,调用栈长O(logn))
散列表

使用散列函数和数组可以构建散列表,散列表是包含额外逻辑的数据结构。
但是要编写出完美的散列函数几乎不可能,假如给两个键分配的空间相同的话就会出现冲突。如何处理冲突呢?最简单的办法是:假如在某一空间上产生冲突,就在这一空间后再加上一个链表。但是假如这个链表很长,会很影响查找的速度(链表只能顺序查找,查找时间为O(n))
所以一个能尽量避免冲突的散列函数是多么重要,那么怎么编写一个性能较高的散列表呢?
较低的填装因子(一旦填装因子大于0.7,就需要调整长度)
良好的散列函数(让数组中的值呈均匀分布,可以了解下SHA函数)
广度优先搜索

广度优先搜索能够解决两个问题:
两个节点之间是否存在相连的路径
最短的距离是多少?这个“最短距离”的含义有很多种。
想象这么一个问题:你想在你的微信好友和好友的好友中寻找是否有人是一名消防员,该如何查找?并且尽可能这人和你的关系更近些。
迪克斯特拉算法

在图中,搜索最小的“段”数可以用广度优先算法,这就相当于默认每条边的权重是相同的,如果每条边的权重不同呢?那就需要用到迪克斯特拉算法。
概括来说,迪克斯特拉算法就是从起点开始,首先寻找最廉价的节点,更新其开销并标记为已处理,然然后在未处理的节点中寻找开销最小的节点,然后以此往复下去。
针对书中的这样一个问题,我把题干提取出来:目标是用乐谱换钢琴。现在乐谱可以免费换海报;海报加30元换吉他;海报加35元换架子鼓;乐谱加5元可以换唱片;唱片加15元换吉他;唱片加20元换架子鼓;吉他加20元换钢琴;架子鼓加10元换钢琴。
现在我用图把这个关系表示出来:
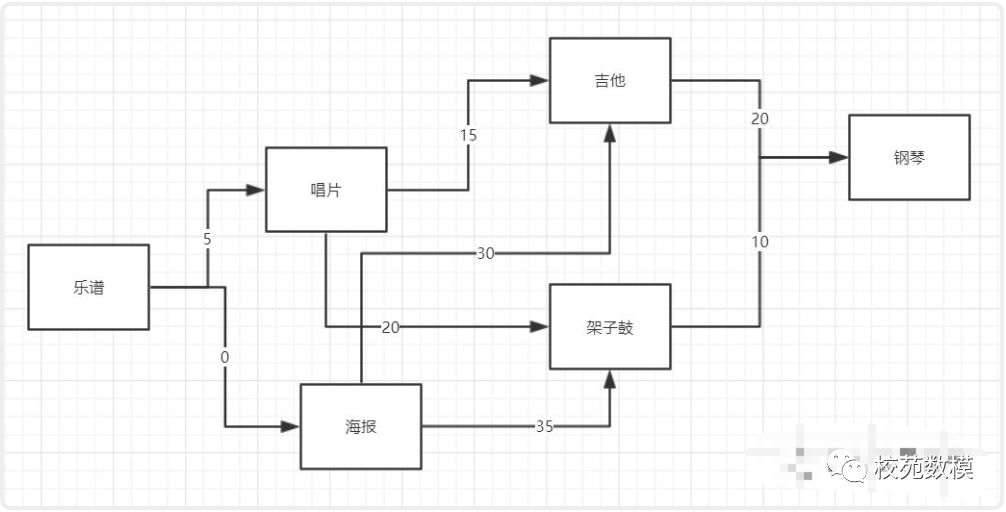
可以看出这是一个加权图,现在我们要使用迪克斯特拉算法寻找最短路径。
最后的最低开销表为:
节点
开销
海报 | 0 |
唱片 | 5 |
吉他 | 20 |
鼓 | 25 |
钢琴 | 35 |
父子节点表为:
父节点
子节点
乐谱 | 唱片 |
乐谱 | 海报 |
唱片 | 吉他 |
唱片 | 鼓 |
鼓 | 钢琴 |
可以看出,最优的交换的路径为:piano-drum-record-music
最低开销为:35元
贝尔曼-福德算法

在迪克特拉斯算法的基础上,我们考虑这样一种情况,假如边的权重存在负值。
在迪克特拉斯算法中,我们首先寻找最廉价的节点,更新其开销,再寻找未处理节点中最廉价的节点,以此往复。
可能出现这样一个情况:
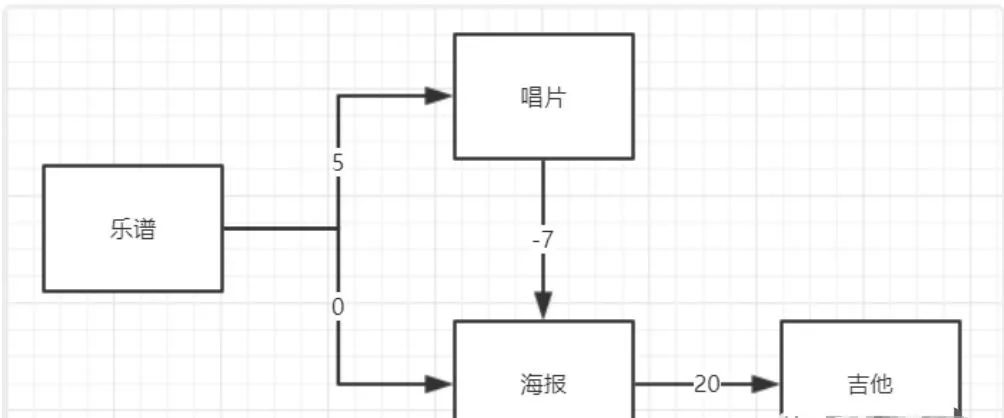
在将海报标记为已处理后,开始处理唱片,但是唱片到海报的路径使得海报的开销更小,又将更新海报的开销,但是海报已经标记为已处理。那么就会出现一些问题。假如继续使用迪克特拉斯算法,最后的结果肯定是错的,大家可以更改参数试一下。为了正确解决问题,这时需要使用贝尔曼-福德算法。
贪心算法

对于一些比较复杂的问题,使用一些算法不能简单有效地解决,这时候往往会使用贪心算法:每步操作都选择局部最优解,最终得到的往往就是全局最优解。这似乎是想当然的做法,但是很多情况下真的行之有效。当然,贪心算法不适用于所有场景,但是他简单高效。因为很多情况并不需要追求完美,只要能找到大致解决问题的办法就行了。
假如我们面对这么一个问题:假设我开了一家网店,在全国各省都有生意,现在面临发快递的问题,假设现在的基础物流不是很完善,每家快运公司只能覆盖很少几个省,那么我该如何在覆盖全国34个省级行政区的情况下,选择最少的快运公司?

这个问题看似不难,其实很复杂。
现在假设有n家快运公司,那么全部的组合有2^n种可能。
N
2^N
10 | 1024 |
20 | 1048576 |
50 | 1125899906842624 |
可以看到,假如有50家快递公司,我将要考虑1125千亿种可能。可以看到,没有算法能很快的计算出这个问题,那么我们可以使用贪心算法,求局部最优解,然后将最终得到的视为全局最优解。
那么在这个问题下如何使用贪心算法?核心在于什么是局部最优条件?可以这样:
选择一家覆盖了最多未覆盖省的公司。
重复第一步。
来源:果核里的图灵
版权归原作者所有,转载仅供学习使用,不用于任何商业用途,如有侵权请留言联系删除,感谢合作。
数据与算法之美
用数据解决不可能

长按扫码关注



















