全世界只有3.14 % 的人关注了
青少年数学之旅
要说最近人气最火热的游戏，莫过于前段时间刚崛起的“多多自走棋”。
而关于“多多自走棋 ”被讨论得最多的就是，“到底是靠运气还是技术?”
都说吃鸡靠运气，但这些道具加成，在数学计算面前都是渣渣!
毕竟像这种多人在线竞技类PK类游戏，能否站到最后还是得靠脑子，“天胡看运气，吃鸡看技术”就是这个道理。
那么问题来了，多多自走棋到底要怎么玩呢？下面我们就一起来看看吧。
一、游戏机制
首先，这是一款通过集换棋子卡牌、棋子排列和旗子对战的八人对战游戏，在游戏中每位棋手通过在商店购买棋子，在棋盘上排兵布阵组建自己的队伍阵容，随机进攻敌方阵容。
棋子分为战士、法师、牧师、术士、猎人、工匠、德鲁伊、骑士、萨满、潜行者、猎魔人11种职业，共有63种棋子。
二、游戏目标
当玩家防守失败后，就会根据进攻方剩余棋子数量和等级，对玩家扣除一定的血量；血量为0即被淘汰，留到最后就是大家常说的吃鸡。
三、棋子进化与羁绊
玩家在每回合比赛开始时，棋子商店会自动刷新5个棋子，我们可以通过金币去刷新棋子，同时棋子分为1星、2星和3星，3个1星可以合成1个2星，3个2星可以合成1个3星。
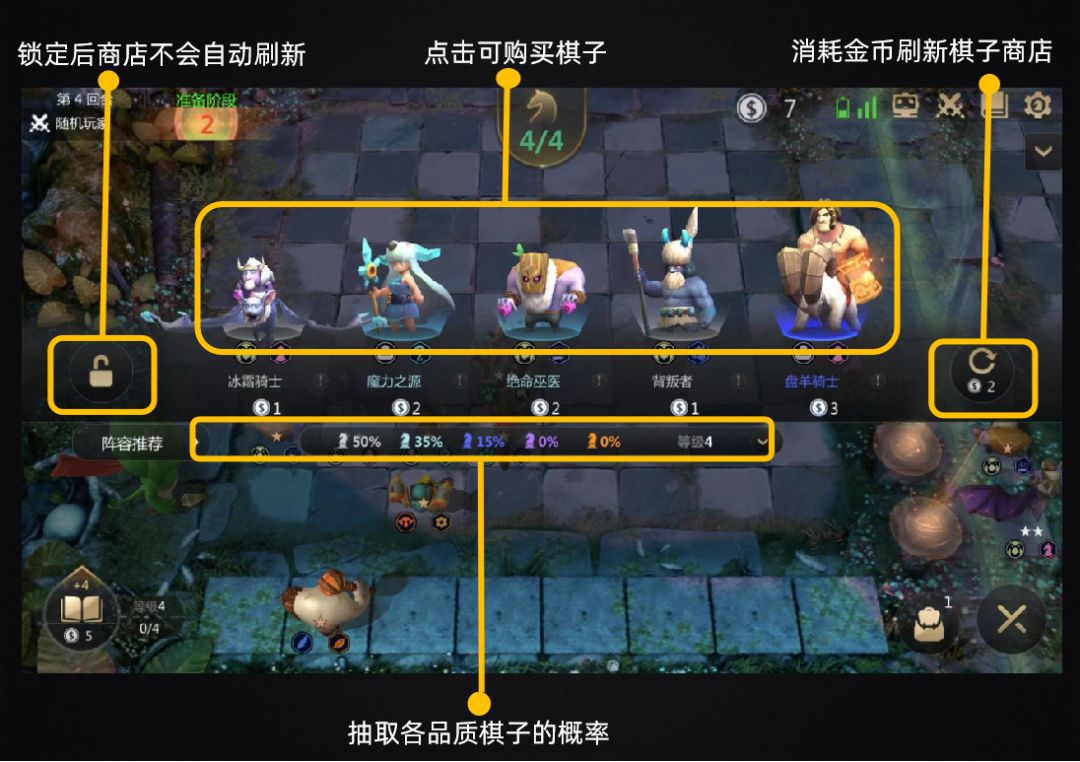
手动刷棋
简单来说，多多自走棋其实就是一个通过组建自己阵容淘汰对手的吃鸡游戏。你可以精心排兵布阵，也可以听天由命靠欧皇。
所谓欧皇，就是指那种在卡牌收集游戏或者类似的游戏里，手气特别好。欧皇附体就是指这一次的运气特别好。
说到这里，可能有模友会问，“这也不难吧?靠欧皇就行啦......”
多多自走棋虽看似简单，但它其实是一款策略烧脑类游戏，而且我猜很多玩家肯定没思考过自己为啥那么快就死了，甚至现在都还一直认为这是一款欧皇游戏......
所以，为了帮助各位模友们排难解惑，把把吃鸡，本着助人为乐的超模君决定深入敌军，一探究竟。
于是，我又通宵了......
这黑眼圈是怎么肥事
数学角度告诉你，吃鸡还得靠策略
经过上百个回合的奋战之后，超模君发现，欧皇对吃鸡确实有帮助，但“欧皇不会常在，策略才是硬本领。”
因为谁都不能保证次次都能抓到相同的棋子，而对局思路更能成为吃鸡的关键，“三分天注定，七分靠打拼”说的就是这个道理。
不听不听，王八念经
欧皇
就像一张麻将桌总有赢家，总有输家，但是你如何能够保证你在这张桌子上尽可能收益最大化，那就是你的技术了。
“看智商。”
此话怎讲？
一、观察发牌员的意愿（刷牌概率）
首先我们要清楚，想要稳定胜率上分的话，千万不能有“我一定要玩XX流派”的想法，因为每把多多自走棋都是一个新的开始，我们要学会有策略的刷牌拿牌。
费=金币，即一费就是一金币
我们知道，从一费到五费，每种类型的棋子出现的概率是不一样的，那我们如何知道是否可以刷到我们想要的棋子呢？
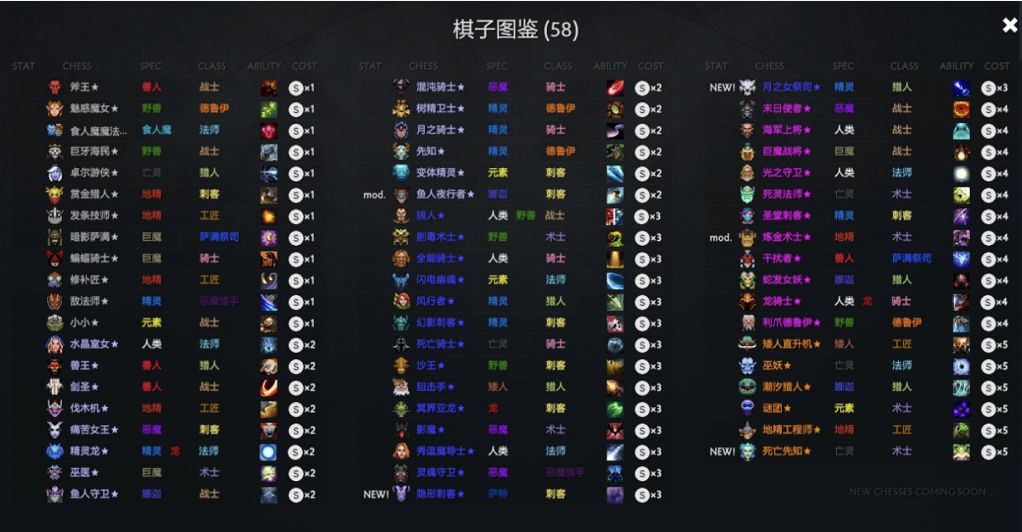
以这张棋子图鉴为例展开
我们设x为一种紫色棋子（紫色棋子4费）的数量，a为紫色棋子中”巨魔战将“在场上的数量，而目前紫色棋子类型有11种，设场上有y个紫色棋子（2星=3个，3星=9个，以此类推），z是抽中”巨魔战将“的概率，则有
z={(x-a)/(11x-y)}*5*当前等级紫色棋子的概率
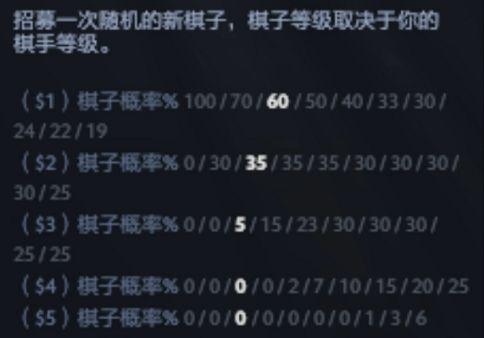
不同等级不同棋子出现的概率
超模君打听到，目前紫色棋子是x=15个，现在假设场上已经有30个紫色棋子，“巨魔战将”有4个，我们棋手的等级是9，即当前等级紫色棋子的概率20%：
棋手等级为9，紫色棋子出现的概率
则单次刷出“巨魔战将”的概率为
z={（15-4）/（11*15-30）}*5*20%
=（11/9*15）*1
=0.0815
即单次刷出“巨魔战将”的概率为8.15%，其他棋子我们都可以类似计算。
猎魔人
而最近盛行的“赌狗流”玩法同样也可以通过计算概率合理D牌：
所谓赌狗流，就是不留钱，有钱尽量花，利用在前期搜卡，快速到达二星或者三星的方法，这个方法收益大，风险也大。
跟天胡狗不同的是，“赌狗流”是在尽量保持概率出牌的情况下去D牌，而“赌狗流”也往往可以锤爆天胡狗，正所谓赌狗一时爽，一直赌狗一只爽。
二、看其它玩家的选择
知道刷牌概率还不行，还要学会看其它玩家走的路线，毕竟“一山不容二虎，除非一公一母。”
我们要观察所有敌方棋子阵容，然后迅速分析出什么流派没有人玩，接下来往那个流派走。哪怕剩下没人玩的流派相对冷门也没关系，毕竟星级才是爸爸。
因为多多自走棋是公共牌库，所以欧皇很难存活，热门棋子别人要花钱搜才能拿到，而冷门棋子可以轻松白嫖。
哪怕冷门流派相对弱势，可如果有一堆3星的大哥照样殴打主流棋组，这就是策略。
三、合理吃利息
这里的利息机制是，当你每拥有10金币，则下回合会多出1金币利息作为奖励，利息最多5金币。
简单来说，就是存到50金币每回合结束会有5金币利息，但是超过50金币也同样是5金币利息！
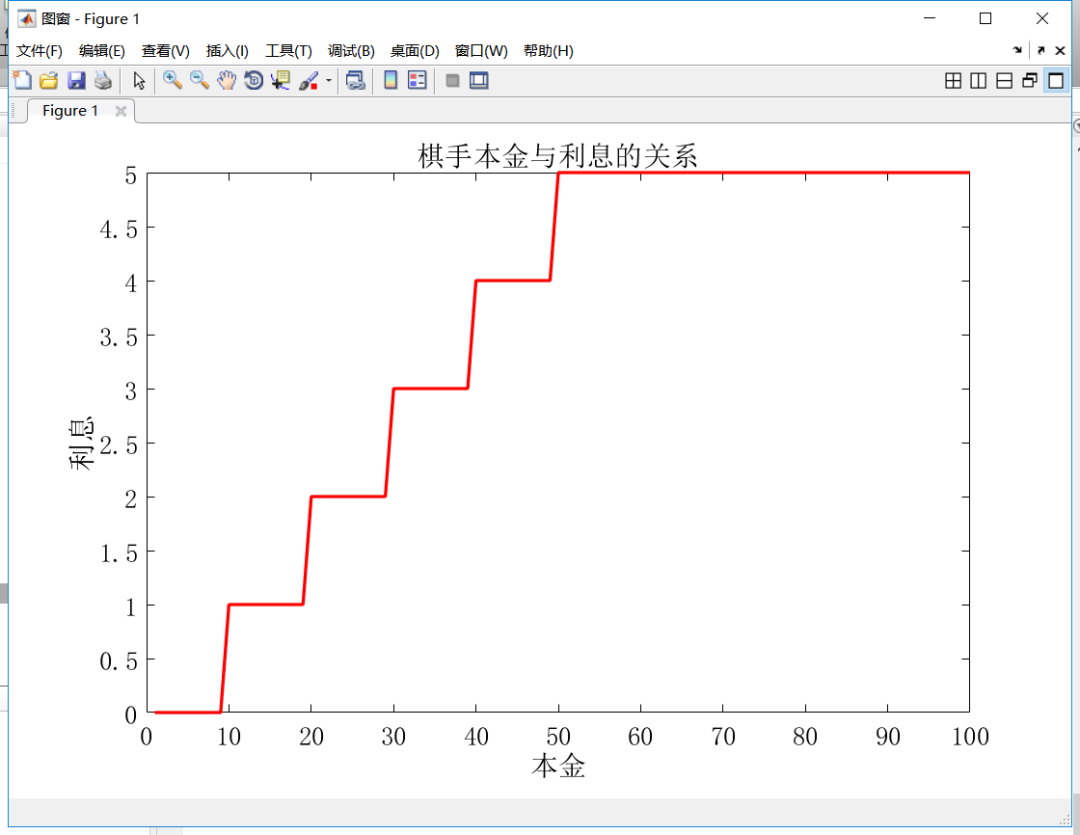
所以，合理吃利息可以在中后期有更多资本去刷自己想要的棋子，增加胜率。
通过精细计算与运营，把握好这些策略点，虽然不能逆天改命把把天胡，但是稳定上分吃鸡还是能做到的。
说到这里，大家都知道能不能吃鸡阵容成型很关键，但阵容成型的基础就是你得有经济，要有经济就得胡牌，那么这时候就要看站位了。
多多自走棋其实是一个博弈论问题
柏拉图曾说：“数学为万物的本质”，而多多自走棋自然也离不开数学，站位问题归根结底来说其实就是一个博弈论问题。
在很早以前，就有不少数学家曾对此类问题进行过深入的研究。
加拿大著名数学家阿尔伯特•塔克就曾提出过类似的“囚徒困境博弈”问题：
博弈论主要研究各结构间的相互作用，考虑游戏中的个体的预测行为和实际行为，并研究它们的优化策略。
囚徒困境博弈 [Prisoner's dilemma]
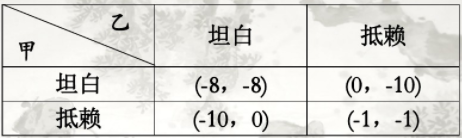
简单来说，就是在未知对方做出选择的情况下，如何做出决策来使自己最优。
对甲来说，尽管他不知道乙作何选择，但他知道无论乙选择什么，他选择"坦白"总是最优的，这就是纳什均衡博弈最优。
纳什均衡(Nash Equilibrium):在一策略组合中，所有的参与者面临这样一种情况，当其他人不改变策略时，他此时的策略是最好的。
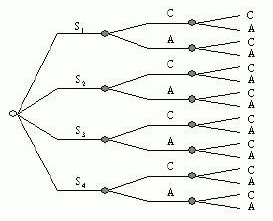
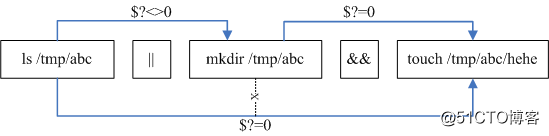
博弈模型的博弈树
而回到下棋本身，一个博弈问题就是，“如何站位最优？”
首先我们要观察对手的站位，到后期只剩下两三个对手时，我们往往可以推算出下一个即将遇到的对手，然后及时调整我们的站位。
调整站位博弈
假设我们博弈如上图所示，很明显，当我们及时做出对策调整站位时，无论对手做何选择，我们都是最优的，也就是说，我们的收益最大化。
再者，假如在某个回合还存活n个棋手，设Q（i)表示下一轮遇到第i位棋手的概率(i=1，2，3.......n)，V、C表示他调整站位前后的胜利概率，则该棋手的实际胜率为
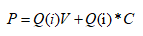
最优化的一阶条件是
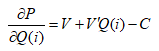
即从单个玩家出发，满足胜利的最优解为
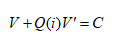
以此类推，其他棋手概率也可类似算出，吃鸡胜率也会大大提升。
而在具体站位调整方面，超模君也总结了相对优势的站法方法：
一、战士站法
众所周知，战士很顶但手短，不说对面有海妖、船长这样的控制一控一大片，就算对手采取缩角落站位也吃不消，很容易就导致一大群人看戏最后被对面团灭。
正确的站位方式：把船长、海妖这些需要快速放技能的团控棋子顶到前排，其余战士靠后，这样既避免了卡棋子的尴尬，又起到了拉散对面阵型的作用。
二、刺客站法
刺客流的刺客站位要全部靠后，因为刺客的攻击机制是攻击范围内没有敌人会大跳至最远敌人的身后进行攻击。
刺客阵容的前排不会太多，一般会采用大树、利爪等优质棋子，同时记得单拉出光羽刺客，其可以吸引一大波火力。
三、法师站法
法师的AOE能力我们是有目共睹的，所以法师一般以拓扑结构站位，形成一个闭合四边形阵容，将法师保护在内围，这也堪称是数学上最美的阵容。
光法、光鳞龙这些拥有线性AOE技能的脆皮单位放在角落才能达到输出最大化，而像蓝胖、电棍这些具有一定坦度的法师则可以放在外围抵御刺客切后。
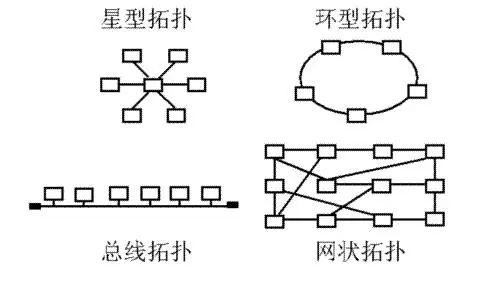
四种不同站位拓扑结构（视具体情况而定）
可以看出，这些站位技巧得分的每一步关键背后都是策略精密推导的结果。
学会这些站位技巧，想不吃鸡都难。
所以，回到最开始那个问题，“天胡看运气，吃鸡看技术”，多多自走棋吃鸡关键还是得靠策略。
当然，这其中还有很多超模君不知道的吃鸡策略，这也期待我们模友们慢慢去发现。
而最近，大家期待已久的双排模式也是终于上线了，想和女友双排玩耍的模友们是不是有点小激动呢。
单身狗的春天
得知消息后，超模君也是马不停蹄地就去甜蜜双排了一波。
经超模君一番推导后，最后总结出了和女友甜蜜双排时，所需策略其实就只有一条：她说什么是什么。
点击【阅读原文】开启你的甜蜜双排之旅吧~
