Improved Deep Metric Learning with Multi-class N-pair Loss Objective

来源：

• NIPS’2016
• NEC Laboratories America

找到这篇论文是因为看了淘宝搜索出品的论文Rethinking the Role of Pre-ranking in Large-scale E-Commerce ¹，文中就提到了传统的list-wise损失 不适用于列表中存在多个正样本的场景。从样本构造的角度来看，这种方式应该也适用于多标签分类。

度量学习一直是我想了解的一个领域，就拿这篇论文做一个开始吧。

Distance Metric Learning

度量学习（metric learning）²，简言之：学习数据的嵌入表示，嵌入具有这样的性质，相似的数据点距离近不相似的数据点距离远。度量学习中常见的两种损失：对比损失和三元组损失，二者形式化的表示：
L c o n t ( x i , x j ; f ) = 1 { y i = y j } ∣ ∣ f i − f j ∣ ∣ 2 2 + 1 { y i ≠ y j } m a x ( 0 , m − ∣ ∣ f i − f j ∣ ∣ 2 ) 2 \mathcal{L}_{cont}(x_i, x_j; f) = \mathbb{1}\{y_i = y_j\}||f_i - f_j||_2^2 + \mathbb{1}\{y_i \neq y_j\}max(0, m - ||f_i - f_j||_2)^2 Lcont​(xi​,xj​;f)=1{yi​=yj​}∣∣fi​−fj​∣∣22​+1{yi​=yj​}max(0,m−∣∣fi​−fj​∣∣2​)2

$${\mathcal{L}}_{tri}(x,x^{+},x^{-};f)=max(0,||f-f^{+}|{|}_2^2-||f-f^{-}|{|}_2^2+m)$$

其中${\mathcal{L}}_{cont}$为对比损失（现在火起来的对比学习），${\mathcal{L}}_{tri}$为三元组损失，$f$表示样本的嵌入。在对比损失中，要求来自同类别的样本距离近，不同类别的样本距离远；三元组损失中要求正($x^{+}$）、负（$x^{-}$）样本到锚点（$x$，如搜图场景中的查询图）的距离要大于一定的阈值。

度量学习有一些现在很常见的应用，例如人脸识别、搜图等。度量学习的样本中通常只有一个负样本，容易导致收敛速度慢和局部最优的问题。难负样本挖掘（提一嘴：随着更多的实践，愈发觉得数据质量的重要性，如何构造好的数据集是一个值得研究的问题）能够减轻这些问题，但是如何找到难负样本本身就是一个难题。

与常见的三元组损失（triplet loss）中一个锚样本、一个正样本和一个负样本不一样，论文提出了一个$(N+1)$元组的损失，来使一个正样本与$N-1$个负样本区分开来。

Deep Metric Learning with Multiple Negative Examples

在三元组损失中，如果要使得损失尽可能低，显然有这么几种情况：

• 缩短正样本与锚样本的距离；
• 增大负样本与锚样本的距离；
• 以上二者的结合。

从三元组损失的计算方式上也可以看出，再一次更新中只会比较锚样本与一个负样本，忽略了其他类别的负样本。这就导致：每次只能使锚样本远离一种负类，或许又被推到其他负类那里去了。最终学习到的嵌入可能会出现这样的情况：锚样本离训练数据中出现较多的负类远，而离某些负类又很近。

当然，我们可以为锚样本配很多个三元组，囊括不同类别的负样本，这样在多轮、充足的训练后嵌入能够具有理想的性质。这样做就面临了不稳定以及收敛速度慢的问题。因此，文中就提出了$N+1$元组的损失，二者的区别如下图所示：

Deep metric learning with (left) triplet loss and (right) (N+1)-tuplet loss.

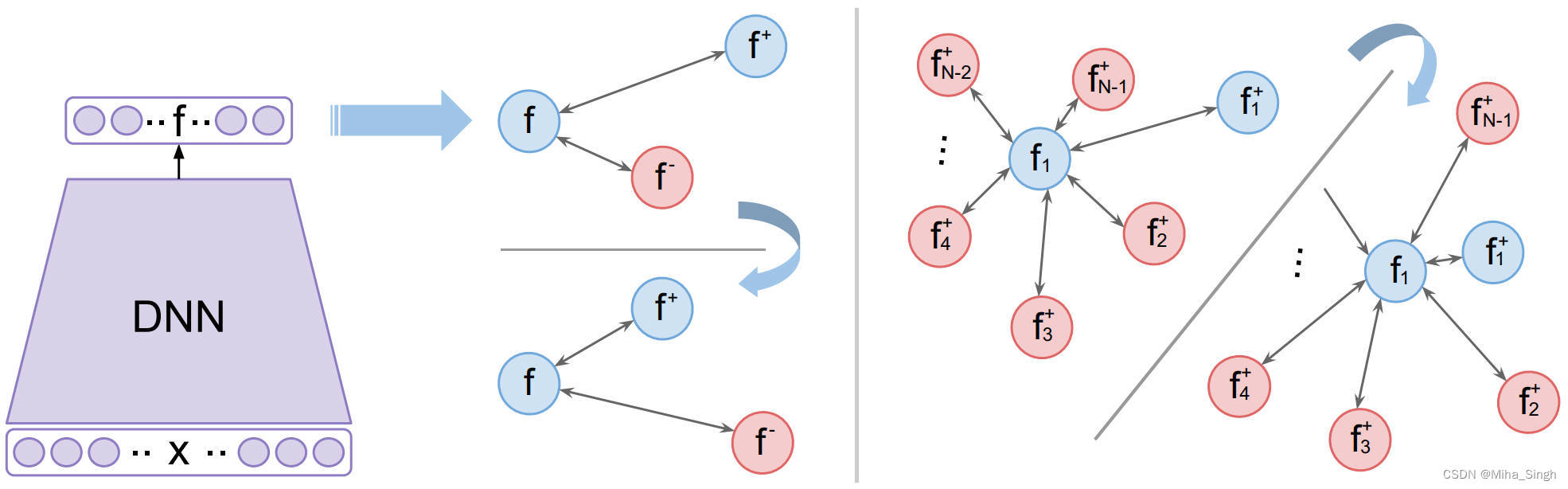
上图中红色的圆表示负样本，蓝色的表示锚样本和正样本。从左侧可以看出，$N+1$元组损失的一个很简单的出发点：既然一个负类的样本不够，那就每个负类都拿一个样本出来，组成一个$N+1$的元组。但是在类别很多的场景（比如人脸识别），计算的复杂度过高。文章的重点就在于如何设计这样一个计算上可行的损失函数。

下图是三元组损失(a)、$(N+1)$元组损失(b)及其改进后的损失©的一个对比。$N$-pair-mc loss（multi-class N-pair loss）损失就是文章最后提出的损失。

Triplet loss, (N+1)-tuplet loss, and multi-class N-pair loss with training batch construction.

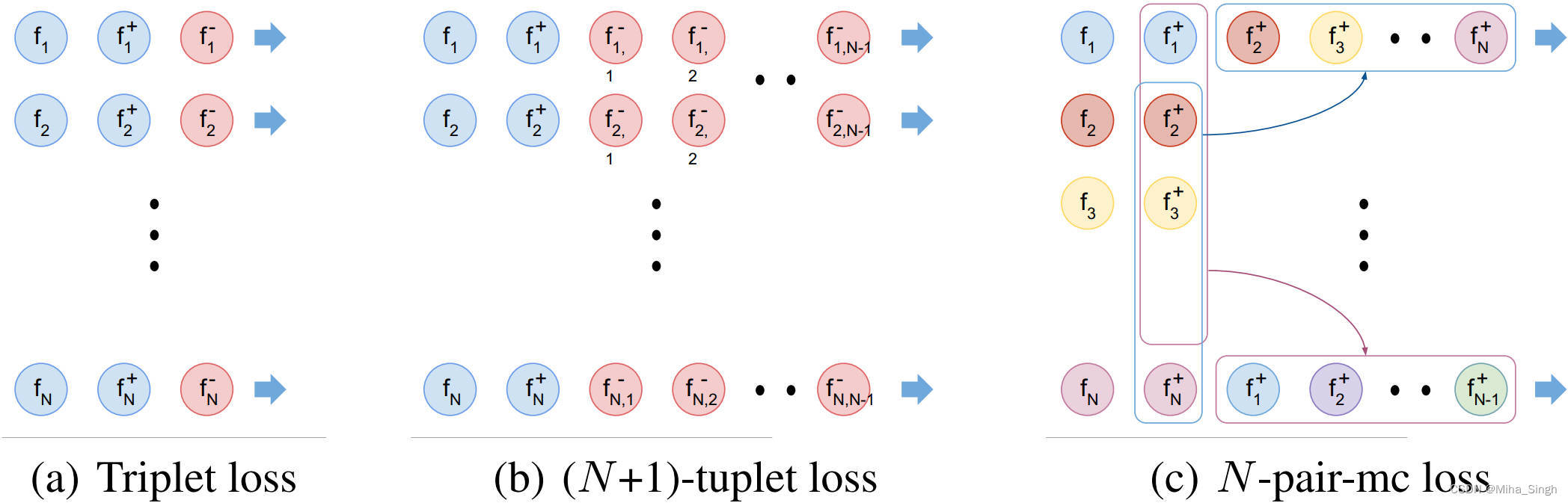
$(N+1)$元组损失可以定义如下：
L ( { x , x + , { x i } i = 1 N − 1 } ; f ) = l o g ( 1 + ∑ i = 1 N − 1 e x p ( f T f i − f T f + ) ) \mathcal{L}(\{x, x^+, \{x_i\}_{i=1}^{N-1}\}; f) = log(1 + \sum_{i=1}^{N-1} exp(f^T f_i - f^T f^+)) L({x,x+,{xi​}i=1N−1​};f)=log(1+i=1∑N−1​exp(fTfi​−fTf+))
当$N$等于2的时候该损失是与三元组损失等价的。提一嘴，这个形式和softplus的形式是一样的：
$$softplus(x)=log(1+exp(x))$$
$(N+1)$元组的损失可以写为如下形式：
$$log(1+\sum _{i=1}^{N-1}exp(f^T{f}_i-f^T{f}^{+}))=-log\frac{exp(f^T{f}^{+})}{exp(f^T{f}^{+})+{\sum }_{i=1}^{N-1}exp(f^T{f}_i-f^T{f}^{+}))}$$
这样一看是不是就更顺眼了，这不就是多分类里的softmax loss嘛。

N-pair loss for efficient deep metric learning

论文提出了一种高效的批构造方法，以降低额外的计算开销。方法的名字叫multi-class $N$-pair loss($N$-pair-mc)，其构造方式如上图 ( c )所示。来个说文解字，道一道作者的解决方法。方法名中有个N-pair，就从这入手。假若我们有$N$个pair:
$$\{(x_1,x_1^{+}),\cdots ,(x_N,x_N^{+}\},y_i\ne y_j,\forall i\ne j$$
每个pair的样本来自不同的类别，在这$N$个pair的基础上构建$N$个元组 { S i } i = 1 N \{S_i\}_{i=1}^N {Si​}i=1N​，其中：
S i = { x i , x 1 + , x 2 + , ⋯ , x N + } S_i = \{x_i, x_1^+, x_2^+, \cdots, x_N^+\} Si​={xi​,x1+​,x2+​,⋯,xN+​}
其中$x_i$就是锚样本。显然，$S_i$就是一个包含了一个$i$类别正样本，$N-1$个其他类别负样本的$N+1$元组了。因此，对于一个由$N$个查询组成的batch，只需要准备$2N$个样本，即$N$个锚样本和$N$个对应类别的正样本，每个batch只需要**$2N$次前向计算**样本的嵌入就可以了。而在三元组损失和$N+1$元组损失中分别是$3N$和$(N+1)N$。因此，对于$N$个查询组成的batch，其损失可以如下计算：
$${\mathcal{L}}_{N-pair-mc}(\{(x_i,x_i^{+}{\}}_{i=1}^N;f)=\frac{1}{N}\sum _{i=1}^{N}log(1+\sum _{j\ne i}exp(f_i^T{f}_j^{+}-f_i^T{f}_i^{+}))$$
以上就是论文的主要内容了，当然论文中还提到了负类别挖掘，这个就暂且不提了。

总结

简言之，这篇论文将度量学习中常见的三元组损失中只有一个负样本扩展到每个样本中包含$N-1$个负样本，并且为了计算的效率提出了$N$-pair的batch构造方法以降低计算量。其实，如果在三元组损失的batch中精心设计各种类别样本的配比，比如每个batch只训练一个类别，是否也能达到类似的效果呢？

参考

---

1. Rethinking the Role of Pre-ranking in Large-scale E-Commerce, KDD 2023. ↩︎

2. 漫谈-Distance Metric Learning那些事儿：https://zhuanlan.zhihu.com/p/458114525. ↩︎