文章目录
- 邻接矩阵存储图的广度优先遍历过程分析
- C语言实现队列编程
- 程序中加入图的处理函数
- 结果的再次分析
- C#语言实现图的广度优先遍历、并显示广度优先遍历生成树
- JavaScript语言实现图的广度优先遍历、并显示广度优先遍历生成树
邻接矩阵存储图的广度优先遍历过程分析
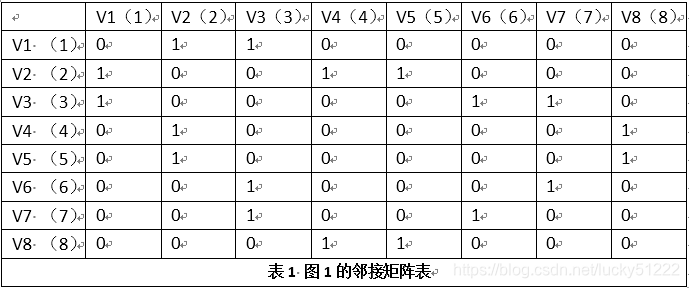
对图1这样的无向图,要写成邻接矩阵,则就是下面的式子

 一般要计算这样的问题,画成表格来处理是相当方便的事情,实际中计算机处理问题,也根本不知道所谓矩阵是什么,所以画成表格很容易帮助我们完成后面的编程任务。在我们前面介绍的内容中,有不少是借助着表格完成计算任务的,如Huffman树。
一般要计算这样的问题,画成表格来处理是相当方便的事情,实际中计算机处理问题,也根本不知道所谓矩阵是什么,所以画成表格很容易帮助我们完成后面的编程任务。在我们前面介绍的内容中,有不少是借助着表格完成计算任务的,如Huffman树。
为了记录那些顶点是已经走过的,还要设计一个表来标记已经走过的顶点,在开始,我们假设未走过的是0,走过的是1,于是有:

对广度优先遍历,还需要补充一个队列、来记录一个顶点可以抵达到的其他顶点。
广度优先遍历过程如下:
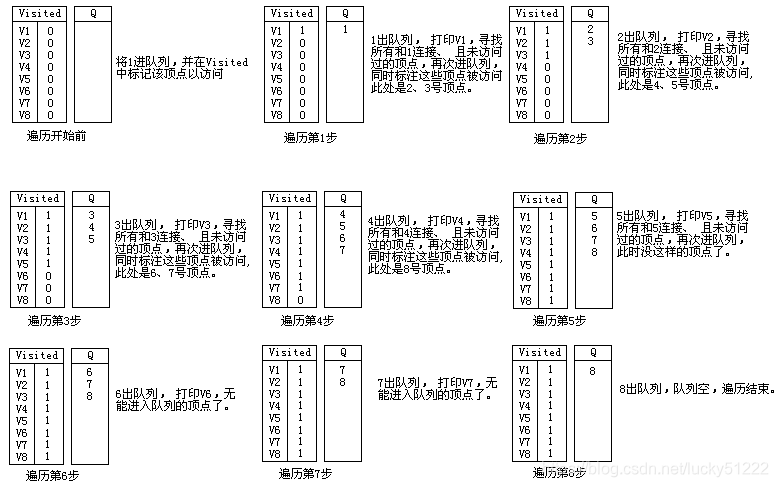
结果分析
从上面的过程可以看出:仅仅就顶点访问到的次序而言,图1的广度优先遍历结果是:
V1->V2->V3>V4->V5->V6->7->V8
但实际执行过程中我们可以发现:所谓图的广度优先遍历、其结果应该是一个树:
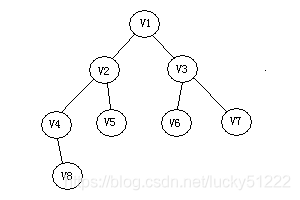
在C语言中,显示这个结果并不容易,所以大多C语言的教材中并不会给出这样的结果。
C语言实现队列编程
根据上面的分析,我们可以知道:要广度优先遍历图,首先要一个队列系统。
队列在C语言上只能自己构造,好在我们前面有链表、有顺序表,我们可以复制过来一个链表程序构造一个队列,于是从链表程序中复制过来b5.c或者b6.c即可,我们分析队列的ADT可知,最需要的队列功能需求是:
QueueInit()、EnQueue、DeQueue()、QueueEmpty()这4个函数,于是有以下队列定义:
struct Queue
{struct LinkedList * LinkQueue;int Count;
};由于我们已经确定使用链表做队列,所以队列实际就是链表的换名包装,所以我们可以理解为队列就是链表的另一种应用,表3的程序就是这样的做法,所以对队列的初始化,就是:
struct Queue * QueueInit()
{struct Queue *q;q=(struct Queue *)malloc(sizeof(struct Queue));q->LinkQueue=LinkedListInit(); q->Count=0; return q;
}有了队列的初始化,则进入队列、实际相当于给这个链表追加一条记录,就是Append()的另类包装:
int EnQueue(struct Queue *Q,struct ElemType *E)
{if(Q==NULL) return -1;if(E==NULL) return -2;Append(Q->LinkQueue,E);Q->Count++; return 0;
}
注意数据出队列,出队列总是把链表中第一个结点的数据给出来、并删除第一个结点,所以出队列就是:
int DeQueue(struct Queue *Q,struct ElemType *E)
{struct ElemType *pE;if(Q==NULL) return -1;if(E==NULL) return -2;pE=LinkedListGet(Q->LinkQueue,1);ElemCopy(pE,E); LinkedListDel(Q->LinkQueue,1); Q->Count--;return 0;
}出队列函数总是把第一个结点删除掉,注意队列完全可能数据出完后再次有数据进入队列,则原来的结点删除函数有Bug,这在程序开发中很正常,修改后就是:
int LinkedListDel(struct LinkedList *L,int n)
{int i;struct Node *p0,*p1;if(L==NULL) return -1;if(n<0||n>L->Count) return -2;p0=L->Head;for(i=0;i<n-1;i++) p0=p0->next;p1=p0->next;p0->next=p1->next;free(p1);L->Count--;if(L->Count==0) L->Tail=L->Head; return 0;
}修改的这个链表结点函数、仅仅加了第14行,在过去,所以结点删除后,最后的尾巴结点指针Tail所指的存储空间被释放,导致这个指针变量不可用,现在在结点个数为0的情况下,再次让尾结点指向头结点,保证下次进入链表的数据依然正确。
而判断队列是否为空则相对简单的多,就是:
int QueueEmpty(struct Queue *Q)
{if(Q==NULL) return -1;return !(Q->Count);
}
补充main()函数,测试多批次进入队列、出队列,全部程序见B0.c
在我们的图遍历应用中,我们对队列的数据仅仅要求一个整数即可,而这个程序进出队列的数据有三列数据,为加强该程序可靠行,修改ElemType(),就是:
void ElemCopy(struct ElemType *s,struct ElemType *d)
{d->sNo=s->sNo;//strcpy(d->sName,s->sName);//d->sAge=s->sAge;
}在一个系统中,类似这样的修改很正常,使用已有的程序完成自己的工作,会大大加快编程的进度,使得编程工作更加流畅。
而这一切都需要自己有足够的积累,有这个积累后完成这样的工作才有基础,所谓技术水平,就是不断积累的过程。
下面,在图的处理中会再次体现这样的过程。
程序中加入图的处理函数
我们的队列系统完成后,记着再复制一个文件,加入图的邻接矩阵读数据程序,我们这里这个程序名称是b1.c。对邻接矩阵数据的读取、并构造图的过程,在深度优先遍历程序中已完成,所以直接复制过来即可,回顾广度优先遍历算法,就是把第一个顶点先无条件装进队列,所以编写遍历BFSM函数如下:
四、程序中加入图的处理函数
我们的队列系统完成后,记着再复制一个文件,加入图的邻接矩阵读数据程序,我们这里这个程序名称是b1.c。对邻接矩阵数据的读取、并构造图的过程,在深度优先遍历程序中已完成,所以直接复制过来即可,回顾广度优先遍历算法,就是把第一个顶点先无条件装进队列,所以编写遍历BFSM函数如下:
void BFSM(struct Graph *G)
{int i,n;struct Queue *Q;struct ElemType *p,E,e;Q=QueueInit(); E.sNo=0; // 设置0进队列EnQueue(Q,&E);G->Visited[0]=1; // 设置0号顶点已被访问p=&e;while(!QueueEmpty(Q)){//待补充}
}从第11行开始,则进入真正的遍历。
有这么个函数后,我们可以补充main()的测试函数就是:
main()
{struct Graph *G;G=GraphCreat("p176G719.txt");BFSM(G);
}main()很短,也很简单,如有不明白的回顾下深度优先遍历函数。
回顾一下:就是队列Q里出队列,然后找与该顶点相连的所有顶点、在进队列,就是:
void BFSM(struct Graph *G)
{int i,n;struct Queue *Q;struct ElemType *p,E,e;Q=QueueInit(); E.sNo=0;EnQueue(Q,&E);G->Visited[0]=1; p=&e;while(!QueueEmpty(Q)){DeQueue(Q,p);n=p->sNo;printf("%s\n",G->pV[n]);for(i=0;i<G->num;i++)if(G->pA[n][i]==1&&G->Visited[i]==0){G->Visited[i]=1; E.sNo=i;EnQueue(Q,&E);}}
}运行这个程序、就会打印出这个图的广度优先遍历结果。
结果的再次分析
有了这个函数后,构造main()开始从第0个顶点遍历图1,就是:
进一步测试该函数,按图1的数据仔细分析下它的执行过程,如有图的连接分量不为1,则会在第一个连接分量遍历完成后终止。如下图4,在B1.C中是无法全部遍历完成的。这个图的文件在G4.TXT,修改表23中第5行,从G4.TXT中读数据,则会发现这个程序仅仅遍历了A、B、C、D,而没有到达过E、F、G这三个顶点。
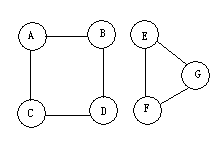
这个图该如何遍历呢?请同学们自己修改程序,完成这个图的遍历。
广度优先遍历到此结束。
C#语言实现图的广度优先遍历、并显示广度优先遍历生成树
在C#文件夹中可以找到“Graph0.cs”,这个文件中包含着深度优先遍历、广度优先遍历等程序中的所有图类程序,现在,我们就要在这个类中补充新的方法。
首先复制这个类到Graph.cs,然后用C#建立一个Windows应用程序,然后在资源管理器中添加这个类,这个类和在深度优先遍历中的类完全一致,但去掉了命名空间说明,这样,这个类就可以使用在其他工程中了。
首先是再次熟悉这个类中的变量定义:
private int[,] A //邻接矩阵
private string[] V //顶点矩阵
private int[] Visited //顶点访问表
private TreeNode[] T //遍历生成树
private int num //顶点个数
private int ConnComp //连通分量
找到这个类中的最后一个方法:DSFTraverse(),然后开始在这个方法后补充新方法:DFS(),由于算法和C语言完全一致,此处算法问题不在介绍。
private void BFS(int N)
{int n;Queue<int> Q = new Queue<int>();Q.Enqueue(N);Visited[N] = 1; while (Q.Count != 0){n = Q.Dequeue();for (int i = 0; i < num; i++)if (A[n, i] == 1 && Visited[i] == 0){T[n].Nodes.Add(T[i]); Visited[i] = 1; Q.Enqueue(i);}}
}这个方法可以从第N个顶点开始遍历,同前面涉及的问题一样,考虑到多次遍历、以及多连通分量的图,我们还要补充下面的方法:
public int BFSTraverse(){int i;ConnComp = 0;for (i = 0; i < num; i++){T[i] = new TreeNode(V[i]);Visited[i] = 0;}for (i = 0; i < num; i++)if (Visited[i] == 0){BFS(i);ConnComp++;}return ConnComp; }补充完类Graph中两个方法补充后、就可以进行界面设计,设计界面如下:
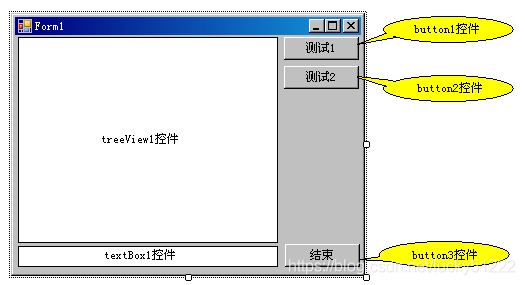
根据图1的界面设计,则广度优先遍历程序中连通分量为1的图在button1下,于是有:
private void button1_Click(object sender, EventArgs e)
{int m;int[,] A = {{0, 1, 1, 0, 0, 0, 0, 0},{1, 0, 0, 1, 1, 0, 0, 0},{1, 0, 0, 0, 0, 1, 1, 0},{0, 1, 0, 0, 0, 0, 0, 1},{0, 1, 0, 0, 0, 0, 0, 1},{0, 0, 1, 0, 0, 0, 1, 0},{0, 0, 1, 0, 0, 1, 0, 0},{0, 0, 0, 1, 1, 0, 0, 0}};string[] V = { "V1", "V2", "V3", "V4", "V5", "V6", "V7", "V8" };Graph G = new Graph(8);G.Arc = A; G.Vertex = V;m = G.BFSTraverse(); treeView1.Nodes.Clear();treeView1.Nodes.Add(G.DFSResult);textBox1.Text = "该图连接分量为" + m.ToString();
}由于类设计中、广泛使用了原有的代码,所以这段程序看起来和深度优先遍历的测试代码差别很小。同理,在有多个连通分量的情况下,在button2下的代码是:
private void button2_Click(object sender, EventArgs e){int m;int[,] A = {{0, 1, 1, 0, 0, 0, 0},{1, 0, 0, 1, 0, 0, 0},{1, 0, 0, 1, 0, 0, 0},{0, 1, 1, 0, 0, 0, 0},{0, 0, 0, 0, 0, 1, 1},{0, 0, 0, 0, 1, 0, 1},{0, 0, 0, 0, 1, 1, 0}};string[] V = { "A", "B", "C", "D", "E", "F", "G" };Graph G = new Graph(7);G.Arc = A; G.Vertex = V;m = G.BFSTraverse(); treeView1.Nodes.Clear();G.AddInTreeView(treeView1);textBox1.Text = "该图连接分量为" + m.ToString(); }请自行补充button3下的代码。
程序运行结果就是:
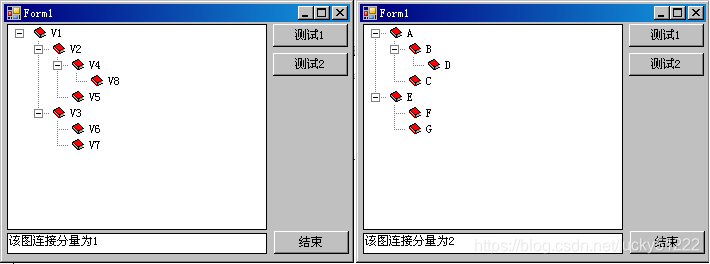 图的广度优先遍历到此结束。通过上述编程我们可以发现:大量使用已有的代码,可以大大简化编程的复杂程度。
图的广度优先遍历到此结束。通过上述编程我们可以发现:大量使用已有的代码,可以大大简化编程的复杂程度。
问题:
我们在C#的程序中、并没有使用类似C语言那样的技术:在数据文件中保存图的数据,这首先是基于我们对C#的使用方式造成的,C#最重要的应用场合是连接数据库服务器和前端的用户浏览器,这个场合下C#提供一个正确的运算类就足够了,其数据要来自于数据库,而结果要给到浏览器上的程序。浏览器下的程序就是JavaScript,这样的情况下C#不做数据文件读取、而要做的是数据库上数据读取,至于送到JavaScript,这个对C#、就要通过一种叫WebService的技术,而在JavaScript上、则要用到一种叫Ajax技术读写这些数据,而这些都是下学期的重要实验任务。
JavaScript语言实现图的广度优先遍历、并显示广度优先遍历生成树
对JavaScript而言,是没有队列类的,尽管数组的类型直接泛型,但仅有栈而无队列。我们需要最低代价完成一个队列系统,所以要再次查看JavaScript数组的所有方法和属性:
其中:FF: Firefox, IE: Internet Explorer
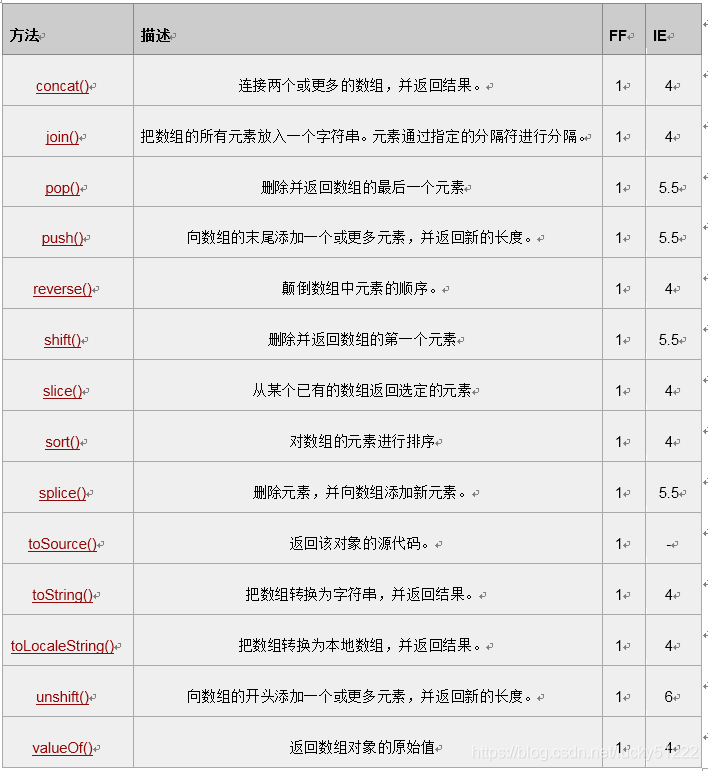
而这个对象提供的属性,则如下表:FF: Firefox, IE: Internet Explorer

回顾栈和队列的差异,一个是先进后出、一个是先进先出,查找上述数组的方法,有个方法是reverse(),含义是颠倒数组元素的次序,很显然:
如果进队列是数组的push()操作,那么出队列则就是颠倒数组次序、然后pop()操作,有这个思路,按这个算法构造队列类就是:
function Queue(){this.Q=new Array();this.EnQueue=function(E){this.Q.push(E);}this.DeQueue=function(){var E;this.Q=this.Q.reverse();E=this.Q.pop();this.Q=this.Q.reverse();return E;}this.Count=function(){return this.Q.length;}}一定注意这个类的第13行,颠倒次序出栈后一定要再次颠倒这个数组的次序,保证进栈数据的次序。这样,我们就用最小代价完成了一个队列系统,然后补充多次进出队列的测试网页,就是:
<html><head><meta http-equiv="Content-Type" content="text/html; charset=gb2312" /><title>一个调用Ext类库的模板页面</title><script type="text/javascript" src="Queue.js"></script><script type="text/javascript" src="ext-3.0.0/adapter/ext/ext-base.js"></script><script type="text/javascript" src="ext-3.0.0/ext-all.js"></script><link rel="stylesheet" type="text/css" href="ext-3.0.0/resources/css/ext-all.css" /> </head><body bgcolor="#FFFFFF"><div id="hello"></div><script type="text/javascript">function fun(){var Q=new Queue();Q.EnQueue(1);Q.EnQueue(2);Q.EnQueue(3);while(Q.Count()>0){document.write(Q.DeQueue()+'<br>');}Q.EnQueue(4);Q.EnQueue(5);while(Q.Count()>0){document.write(Q.DeQueue()+'<br>');}}Ext.onReady(fun);</script></body>
</html>注意第5行一定要引用Queue.js这个文件,否则程序无法运行。
补充广度优先遍历程序
根据广度优先遍历的算法、以及表1的队列对象,不难写出广度优先遍历程序,但写以前我们要回顾深度优先遍历函数的入口参数:
A[][]: 邻接矩阵
vCount: 顶点个数
m: 进入遍历的顶点编号
Visited[] :顶点访问状态表
T[]: Ext.tree.TreeNode对象数组,遍历结果树
我们回顾这些的原因是:我们新的遍历函数、也要尽量和旧的方法使用的参数一致,这样就对后续的编程提供了大量的方便。如果意义相近的方法、其函数入口参数差异很大、这样对后续的编程造成很多困惑。
//A[][]: 邻接矩阵
//vCount: 顶点个数
//m: 进入遍历的顶点编号
//Visited[] :顶点访问状态表
//T[]: Ext.tree.TreeNode对象数组,遍历结果树
function BFS(A,vCount,m,Visited,T)
{var i,n;var Q=new Queue();Q.EnQueue(m);Visited[m]=1;while(Q.Count()>0){n = Q.DeQueue();for (i = 0; i <vCount; i++)if (A[n][i] == 1 && Visited[i] == 0){T[n].appendChild(T[i]);Visited[i] = 1; Q.EnQueue(i);} }
}表3 JavaScript语言图的广度优先遍历,见工程B0.html
该函数算法不在介绍,程序原理和C、C#没什么差别。
从深度优先遍历网页补充广度优先遍历程序
从深度优先遍历网页G8.html复制文件到B0.html,在F3区域的邻接矩阵编辑窗口补充命令按钮“广度优先遍历”,就是表4.
对这个表中的程序,注意是一个程序框架,而不是全部。现在就要在合适的位置补充广度优先遍历的初始化程序。
var grid=new Ext.grid.EditorGridPanel({renderTo:"GRID",title:"图的邻接矩阵编辑",height:400,width:400,cm:colM,store:gstore,tbar: [ { text: "深度优先遍历图", handler: function(){ //已有的深度遍历代码} },{text:"广度优先遍历图",handler: function(){//以下写进遍历的代码} }]
});注意表4,其第20行就是补充广度优先遍历程序的地方,这程序本质就是给BFS()准备合适的数据、并初始化、然后调用BFS()函数,所以这地方和深度优先遍历的代码是一致的,于是有:
text:"广度优先遍历图",
handler: function()
{
//以下写进遍历的代码var m=gstore.getCount();var n=gstore.getAt(m-1).get('row')+1;var Visited=Array();var A=Array();var i,j;for(i=0;i<n;i++){Visited[i]=0;A[i]=Array();T[i]=new Ext.tree.TreeNode({id:vstore.getAt(i).get('id'),text:vstore.getAt(i).get('V')});}for(i=0;i<m;i++){var r=gstore.getAt(i).get('row');var c=gstore.getAt(i).get('col');var v=gstore.getAt(i).get('Value');A[r][c]=v;}var Concom=0;for(i=0;i<n;i++)if(Visited[i]==0) {BFS(A,n,i,Visited,T);Concom++;}var TR=new Ext.tree.TreeNode({id:10000,text:'广度优先遍历树,连通分量'+Concom});for(i=0;i<n;i++)if(T[i].parentNode==null)TR.appendChild(T[i]);treeView1.setRootNode(TR);
}
}和前面深度优先遍历的程序完全一致,仅仅是调用了不同的遍历函数。
遍历网页的进一步修改和完善:构造图类
从B0.html这个网页程序看,首先在两个遍历的命令按钮程序上有大量重复代码,其次是有关图的计算,其邻接矩阵、顶点矩阵、顶点访问状态矩阵、遍历函数等都是分离的变量和函数,而没有构成一个类、从而也就没有图的对象,这样对后续的编程也造成很多不利。
为此,我们要构造一个JavaScript的图类,整体参照C#。
对任何一个语言的类编程而言,都存在数据如何进入对象、以及数据如何从对象里给出这两个基本问题,在使用Ext过程中,我们熟悉了大量的Ext对象属性获得方法,那么我们这里也将按同样的方法来构造类,详细的介绍参见json教程。以下类名称是Graph,其中G是属性参数:
function Graph(G)
{
this.A=G.A;
this.V=G.V;
this.Visited=G.Visited;
this.num=G.num;
this.T=G.T;
}<html><head><meta http-equiv="Content-Type" content="text/html; charset=gb2312" /><title>一个调用Ext类库的模板页面</title><script type="text/javascript" src="G0.js"></script><script type="text/javascript" src="ext-3.0.0/adapter/ext/ext-base.js"></script><script type="text/javascript" src="ext-3.0.0/ext-all.js"></script><link rel="stylesheet" type="text/css" href="ext-3.0.0/resources/css/ext-all.css" /> </head><body bgcolor="#FFFFFF"><div id="hello"></div><script type="text/javascript">function fun(){var G=new Graph({A:[[1,2,3],[4,5,6],[7,8,9]],V:['A','B','C'],Visited:[0,0,0]});}Ext.onReady(fun);</script></body>
</html>注意第16行,其中构造函数的参数里:
{A:[[1,2,3],[4,5,6],[7,8,9]],V:['A','B','C'],Visited:[0,0,0]}
整体构成对象G,进入类后,进入表5程序后,由第3到第5行的程序赋值给对象相应的属性。再次参照表5程序,其中的this,对应在表6的程序是G,广义上,实例化的对象就是表5中的this。
有了上述分析,我们就可以在表5的程序中加入一个公共方法,用来获得属性中V数组的内容,代码就是:
function Graph(G)
{
this.A=G.A;
this.V=G.V;
this.Visited=G.Visited;
this.num=G.num;
this.T=G.T;
this.VName=function(){var i;for(i=0;i<this.num;i++)document.write(this.V[i]);}
}这样写的方法类似是C#中的public void VName(),这样的写法可以在实例对象中引用这样方法,如:
<html><head><meta http-equiv="Content-Type" content="text/html; charset=gb2312" /><title>一个调用Ext类库的模板页面</title><script type="text/javascript" src="G1.js"></script><script type="text/javascript" src="ext-3.0.0/adapter/ext/ext-base.js"></script><script type="text/javascript" src="ext-3.0.0/ext-all.js"></script><link rel="stylesheet" type="text/css" href="ext-3.0.0/resources/css/ext-all.css" /> </head><body bgcolor="#FFFFFF"><script type="text/javascript">function fun(){var G=new Graph({A:[[1,2,3],[4,5,6],[7,8,9]],V:['A','B','C'],Visited:[0,0,0],num:3});G.VName();}Ext.onReady(fun);</script></body>
</html>上述过程完成后,可以加入一个求V数组中每行平均值的方法,涉及到求平均值,首先我们需要一个求指定行和的函数,这个函数定义成私有的,如同表9的程序中的Sum(),私有函数定义和普通的JavaScript函数完全一致。
但在实际使用中,错误首先在第17行,表示this.num是没有定义。
造成这样的结果,主要是私有的函数Sum()并不包含在对象中,这点和C#是完全不一样,所以私有函数中要引用对象的数据,要首先获得该对象的实例,就是要有这样的方法:
var Ob=this;
function Sum()
{
…
for(i=0;i<Ob.num;i++)
…
}function Graph(G)
{
this.A=G.A;
this.V=G.V;
this.Visited=G.Visited;
this.num=G.num;
this.T=G.T;
this.VName=function(){var i;for(i=0;i<this.num;i++)document.write(this.V[i]);}
function Sum(n)
{
var s=0,i;
for(i=0;i<this.num;i++) //私有方法中错误引用对象数据s+=this.A[n][i];
return s;
}
this.AVG=function(n){var s;s=Sum(n)/this.num; }
}function Graph(G)
{
this.A=G.A;
this.V=G.V;
this.Visited=G.Visited;
this.num=G.num;
this.T=G.T;
this.VName=function(){var i;for(i=0;i<this.num;i++)document.write(this.V[i]);}
function Sum(n)
{
var s=0,i;
for(i=0;i<this.num;i++) //私有方法中错误引用对象数据s+=this.A[n][i];
return s;
}
this.AVG=function(n){var s;s=Sum(n)/this.num; }
}function Graph(G)
{
this.A=G.A;
this.V=G.V;
this.Visited=G.Visited;
this.num=G.num;
this.T=G.T;
var Ob=this;
//公共方法
this.VName=function(){var i;for(i=0;i<this.num;i++)document.write(this.V[i]);}
//私有方法
function Sum(n)
{
var s,i;
s=0;
for(i=0;i<Ob.num;i++)s+=Ob.A[n][i];
return s;
}
//公共方法
this.AVG=function(n){var a;a=Sum(n)/this.num; return a;}
}通过上述实验过程,则有两个遍历方法的图类就是:
function Graph(G)
{
this.A=G.A;
this.V=G.V;
this.Visited=G.Visited;
this.num=G.num;
this.T=G.T;
var Ob=this;
//私有方法:深度优先遍历
function DFS(m)
{
var i;
Ob.Visited[m]=1;
for(i=0;i<Ob.num;i++){if(Ob.A[m][i]!=0&&Ob.Visited[i]!=1) {Ob.T[m].appendChild(Ob.T[i]);DFS(i);}}
}
//公共方法:深度优先遍历、以及初始化
this.DSFTraverse=function(){var i,Comcon=0;if (this.num==0||this.num==undefined) return -1;for(i=0;i<this.num;i++){this.Visited[i]=0;this.T[i]=new Ext.tree.TreeNode({id:i,text:this.V[i]}); }for(i=0;i<this.num;i++)if(this.Visited[i]==0){DFS(i);Comcon++;}return Comcon;}
//私有方法:广度优先遍历
function BFS(m)
{var i,n;var Q=new Queue();Q.EnQueue(m);Ob.Visited[m]=1;while(Q.Count()>0){n = Q.DeQueue();for (i = 0; i <Ob.num; i++)if (Ob.A[n][i] == 1 && Ob.Visited[i] == 0){Ob.T[n].appendChild(Ob.T[i]);Ob.Visited[i] = 1; Q.EnQueue(i);} }
}
//公共方法:深度优先遍历、以及初始化
this.BSFTraverse=function(){var i,Comcon=0;if (this.num==0||this.num==undefined) return -1;for(i=0;i<this.num;i++){this.Visited[i]=0;this.T[i]=new Ext.tree.TreeNode({id:i,text:this.V[i]}); }for(i=0;i<this.num;i++)if(this.Visited[i]==0){BFS(i);Comcon++;}return Comcon;}
//获得遍历结果树,适应多个连接分量情况下。
this.getTree=function(){for(i=1;i<this.num;i++)if(this.T[i].parentNode==null)this.T[0].appendChild(this.T[i]);return this.T[0];}
}有了上述图类后,则相应的界面上“深度优先遍历”按钮下的相应程序就是:
text: "深度优先遍历图",
handler: function()
{
//以下写进遍历的代码var m=gstore.getCount();var n=gstore.getAt(m-1).get('row')+1;var Visited=Array();var A=Array();var i,j;for(i=0;i<n;i++){Visited[i]=0;A[i]=Array();}//获得邻接矩阵数据 for(i=0;i<m;i++){var r=gstore.getAt(i).get('row');var c=gstore.getAt(i).get('col');var v=gstore.getAt(i).get('Value');A[r][c]=v;}//获得邻接矩阵数据 var V=new Array();//获得顶点名称for(i=0;i<vstore.getCount();i++)V[i]=vstore.getAt(i).get('V');//用变量给对象各个属性赋值var G=new Graph({A:A,V:V,T:T,num:n,Visited:Visited}); m=G.DSFTraverse();var TR=new Ext.tree.TreeNode({id:10000,text:'深度优先遍历树,连通分量'+m});TR.appendChild(G.getTree()); treeView1.setRootNode(TR);
} 上面仅仅给出深度优先遍历的响应程序,广度优先遍历的代码同上述过程基本一样,仅仅是在第32行处为:m=G.BSFTraverse();
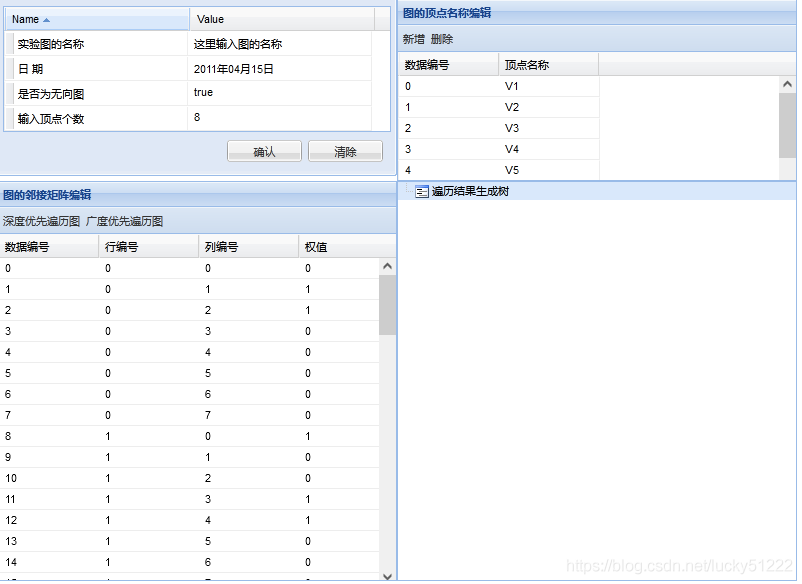
到此,JavaScript的两种遍历全部完成,这里,图的数据来自Ext.data.ArrayStore对象,目前是常数定义或者控件输入,以后还要加入Ajax方法、从C#读远程数据库的数据,这都是下学期的任务了。




![[转]分布式事务之TCC服务设计和实现注意事项](http://pic.xiahunao.cn/[转]分布式事务之TCC服务设计和实现注意事项)


)




)
)

![[转]《吐血整理》系列-顶级程序员工具集](http://pic.xiahunao.cn/[转]《吐血整理》系列-顶级程序员工具集)
)


