二叉树遍历分为三种:前序、中序、后序,其中序遍历最为重要。为啥叫这个名字?是根据根节点的顺序命名的。
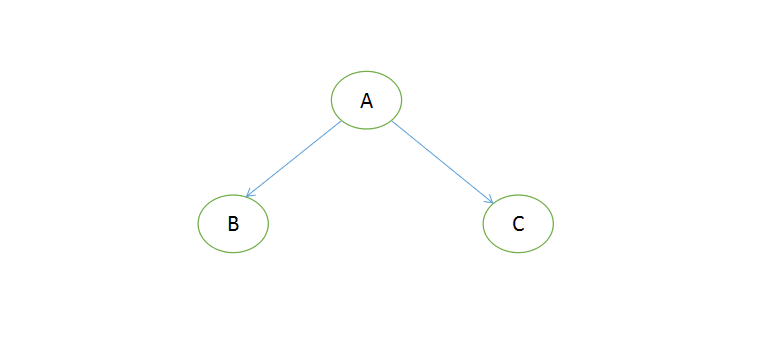
比如上图正常的一个满节点,A:根节点、B:左节点、C:右节点,前序顺序是ABC(根节点排最先,然后同级先左后右);中序顺序是BAC(先左后根最后右);后序顺序是BCA(先左后右最后根)。
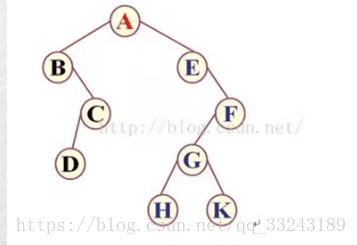
比如上图二叉树遍历结果
前序遍历:ABCDEFGHK
中序遍历:BDCAEHGKF
后序遍历:DCBHKGFEA
分析中序遍历如下图,中序比较重要(java很多树排序是基于中序,后面讲解分析)
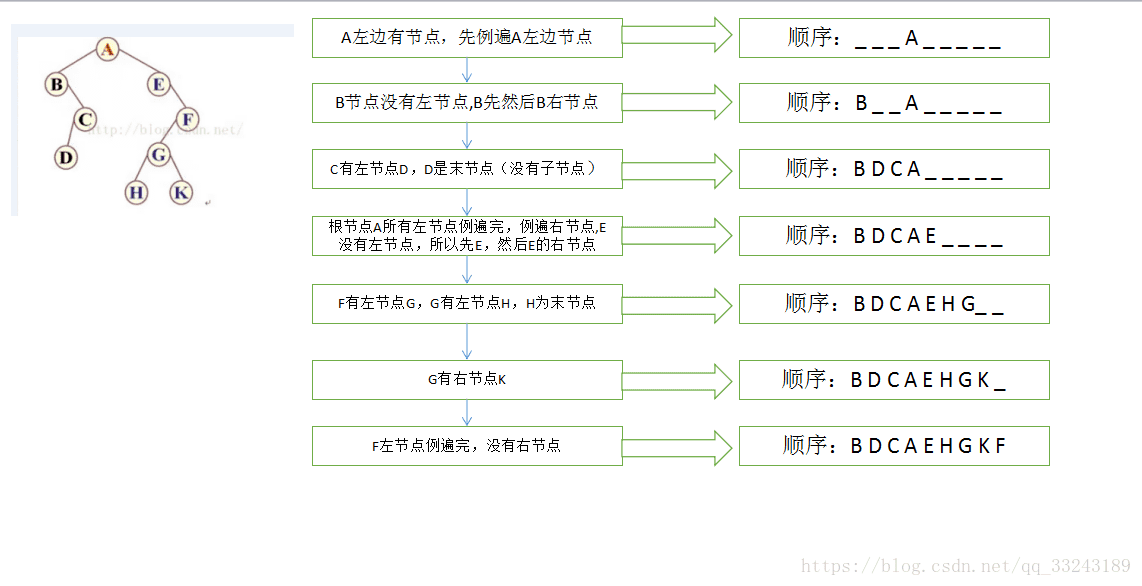
下面介绍一下,二叉树的三种遍历方式,其中每一种遍历方式都有三种实现方式。
节点定义:
struct TreeNode
{
int val;
TreeNode *left,*right;
TreeNode(int val){
this->val = val;
this ->left = this->right = NULL;
}
};
先序遍历
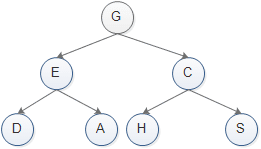
以上面这张图为例:我们讲讲树的三种遍历方式:
先序遍历:先访问根节点,然后访问左孩子,最后访问右孩子。
所以,上面遍历的结果是:GEDACHS。
下面,我们来看看具体代码实现
1.递归实现
void preOrder(TreeNode *root){
if (root==NULL)
return;
cout<val<
preOrder(root->left);
preOrder(root->right);
}
2.使用辅助栈
实现思路:1.将根节点入栈
2.每次从栈顶弹出一个节点,访问该节点
3.把当前节点的右孩子入栈
4.把当前节点的左孩子入栈
具体实现:
void preOrder2(TreeNode *root){
if (root == NULL)
return;
stack stk; //开辟一个栈空间
stk.push(root);
while(!stk.empty()){
TreeNode* pNode = stk.pop();
cout<val;
if (pNode->right!=NULL)
stk.push(pNode->right);
if (pNode->left!=NULL)
stk.push(pNode->left);
}
}
3.Morris遍历
Morris遍历,常数的空间即可在O(n)时间内完成二叉树的遍历。
O(1)空间进行遍历困难之处在于在遍历的子结点的时候如何重新返回其父节点?
在Morris遍历算法中,通过修改叶子结点的左右空指针来指向其前驱或者后继结点来实现的。
其本质:线索二叉树(Threaded Binary Tree),通过利用叶子节点空的right指针,指向中序遍历的后继节点,从而避免了对 stack 的依赖。
具体实现:
void preOrder(TreeNode* root){
if (root == NULL)
return;
TreeNode* pNode = root;
while(pNode != NULL){
if (pNode->left == NULL)
{
cout<val<
pNode = pNode->right;
}
else{
TreeNode* pPre = pNode->left;
while(pPre->right != NULL && pPre->right != pNode){
pPre = pPre->right;
}
if (pPre->right == NULL)
{
/* code */
pPre->right = pNode;
cout<val<
pNode = pNode->left;
}
else{
pPre->right = NULL;
pNode = pNode->right;
}
}
}
}
中序遍历
中序遍历:先访问左孩点,然后访问根节点,最后访问右孩子。
所以,上面遍历的结果是:DEAGHCS。
下面,我们来看看具体代码实现
1.递归实现
void InOrder(TreeNode *root){
if (root==NULL)
return;
InOrder(root->left);
cout<val<
InOrder(root->right);
}
2.使用辅助栈
实现思路:
初始化一个二叉树结点pNode指向根结点;
若pNode非空,那么就把pNode入栈,并把pNode变为其左孩子;(直到最左边的结点)
若pNode为空,弹出栈顶的结点,并访问该结点,将pNode指向其右孩子(访问最左边的结点,并遍历其右子树)
具体实现:
void InOrder(TreeNode *root){
if (root==NULL)
{
return;
}
stack stk;
TreeNode *pNode = root;
while(pNode!=NULL || !stk.empty()){
if (pNode != NULL)
{
stk.push(pNode);
pNode = pNode->left;
}
else{
pNode = stk.pop();
stk.pop();
cout<val<
pNode = pNode->right;
}
}
}
3.Morris遍历
实现思路:
1.如果当前节点pNode的左孩子为空,那么输出该节点,并把该节点的右孩子作为当前节点
2.如果当前节点pNode的左孩子非空,那么找出该节点在中序遍历的前驱结点prev
当第一次访问该前驱结点prev时,其右孩子必定为空,那么就将其右孩子设置为当前结点,以便根据这个指针返回到当前结点pNode中,并将当前结点pNode设置为其左孩子;
当该前驱结点pPre的右孩子为当前结点,那么就输出当前结点,并把前驱结点的右孩子设置为空(恢复树的结构),将当前结点更新为当前结点的右孩子;
3.重复以上两步,直到当前结点为空。
具体实现:
void InOrder(TreeNode *root){
if (root == NULL)
return;
TreeNode* pNode = root;
while(pNode != NULL){
if (pNode->left == NULL)
{
cout<val<
pNode = pNode->right;
}
else{
TreeNode* pPre = pNode->left;
while(pPre->right != NULL && pPre->right != pNode){
pPre = pPre->right;
}
if (pPre->right == NULL)
{
/* code */
pPre->right = pNode;
pNode = pNode->left;
}
else{
pPre->right = NULL;
cout<val<
pNode = pNode->right;
}
}
}
}
后序遍历
后序遍历:先访问左孩子,然后访问右孩子,最后访问根节点。
所以,上面遍历的结果是:DAEHSCG。
下面,我们来看看具体代码实现:
1.递归实现
void PostOrder(TreeNode *root){
if (root==NULL)
return;
PostOrder(root->left);
PostOrder(root->right);
cout<val<
}
2.使用辅助栈
void postOrder(TreeNode *root) {
if(root == NULL)
return;
stack stk;
stk.push(root);
TreeNode *prev = NULL;
while(!stk.empty()) {
TreeNode *pNode = stk.top();
if(!prev || prev->left == pNode || prev->right == pNode) { // traverse down
if(pNode->left)
stk.push(pNode->left);
else if(pNode->right)
stk.push(pNode->right);
/* else {
cout << pNode->val << endl;
stk.pop();
}
*/
}
else if(pNode->left == prev) { // traverse up from left
if(pNode->right)
stk.push(pNode->right);
}
/* else if(pNode->right == prev) { // traverse up from right
cout << pNode->val << endl;
stk.pop();
}
*/
else {
cout << pNode->val << endl;
stk.pop();
}
prev = pNode;
}
}
双辅助栈实现思路:
设置两个栈stk, stk2;
将根结点压入第一个栈stk;
弹出stk栈顶的结点,并把该结点压入第二个栈stk2;
将当前结点的左孩子和右孩子先后分别入栈stk;
当所有元素都压入stk2后,依次弹出stk2的栈顶结点,并访问之。
第一个栈的入栈顺序是:根结点,左孩子和右孩子;于是,压入第二个栈的顺序是:根结点,右孩子和左孩子。
因此,弹出的顺序就是:左孩子,右孩子和根结点。
void PostOrder2(TreeNode *root){ //两个栈实现
if (root == NULL)
return;
stack stk,stk2;
stk.push(root);
while(!stk.empty()){
TreeNode* pNode = stk.top();
stk.pop();
stk2.push(pNode);// 将根节点压栈
if (pNode->left != NULL) // 如果左孩子不为空,则压栈
{
stk.push(pNode->left);
}
if (pNode->right != NULL) // 如果左孩子不为空,则压栈
{
stk.push(pNode->right);
}
}
while(!stk2.empty()){
cout<val<
stk2.pop();
}
}
3.Morris遍历实现
实现思路:
1.先建立一个临时结点dummy,并令其左孩子为根结点root,将当前结点设置为dummy;
2.如果当前结点的左孩子为空,则将其右孩子作为当前结点;
3.如果当前结点的左孩子不为空,则找到其在中序遍历中的前驱结点,
-如果前驱结点的右孩子为空,将它的右孩子设置为当前结点,将当前结点更新为当前结点的左孩子;
-如果前驱结点的右孩子为当前结点,倒序输出从当前结点的左孩子到该前驱结点这条路径上所有的结点。将前驱结点的右孩子设置为空,将当前结点更新为当前结点的右孩子。
4.重复以上过程,直到当前结点为空。
具体实现:
void reverse(TreeNode* p1,TreeNode *p2){
if (p1 == p2)
return;
TreeNode* x = p1;
TreeNode* y = p1->right;
while(true){
TreeNode* tmp = y->right;
y->right = x;
x = y;
y = tmp;
if (x == p2)
break;
}
}
void printReverse(TreeNode* p1,TreeNode *p2){
reverse(p1,p2);
TreeNode* pNode = p2;
while(true){
cout<val<
if (pNode == p1)
break;
pNode = pNode->right;
}
reverse(p2,p1);
}
void PostOrder3(TreeNode* root){
if(root == NULL)
return;
TreeNode *dummy = new TreeNode(-1);
dummy->left = root;
TreeNode *pNode = dummy;
while(pNode != NULL) {
if(pNode->left == NULL)
pNode = pNode->right;
else {
TreeNode *pPrev = pNode->left;
while(pPrev->right != NULL && pPrev->right != pNode)
pPrev = pPrev->right;
if(pPrev->right == NULL) {
pPrev->right = pNode;
pNode = pNode->left;
}
else {
printReverse(pNode->left, pPrev);
pPrev->right = NULL;
pNode = pNode->right;
}
}
}
}
总结
上述三种遍历方式时间复杂度和空间复杂度分析:
1.递归遍历和非递归遍历 时间复杂度0(n) 空间复杂度O(n)
2.Morris遍历 时间复杂度0(n) 空间复杂度O(1)
以上就是本文的全部内容,希望对大家的学习有所帮助,也希望大家多多支持。










![一步步优化JVM六:优化吞吐量[转]](http://pic.xiahunao.cn/一步步优化JVM六:优化吞吐量[转])








