LeetCode—51. N 皇后（困难）

51. N 皇后（困难）

题目描述：
n 皇后问题研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击，即令其中任意两个皇后都不同列、同行和在一条斜线上。

给你一个整数 n ，返回所有不同的 n 皇后问题的解决方案。

每一种解法包含一个不同的 n 皇后问题的棋子放置方案，该方案中 ‘Q’ 和 ‘.’ 分别代表了皇后和空位。
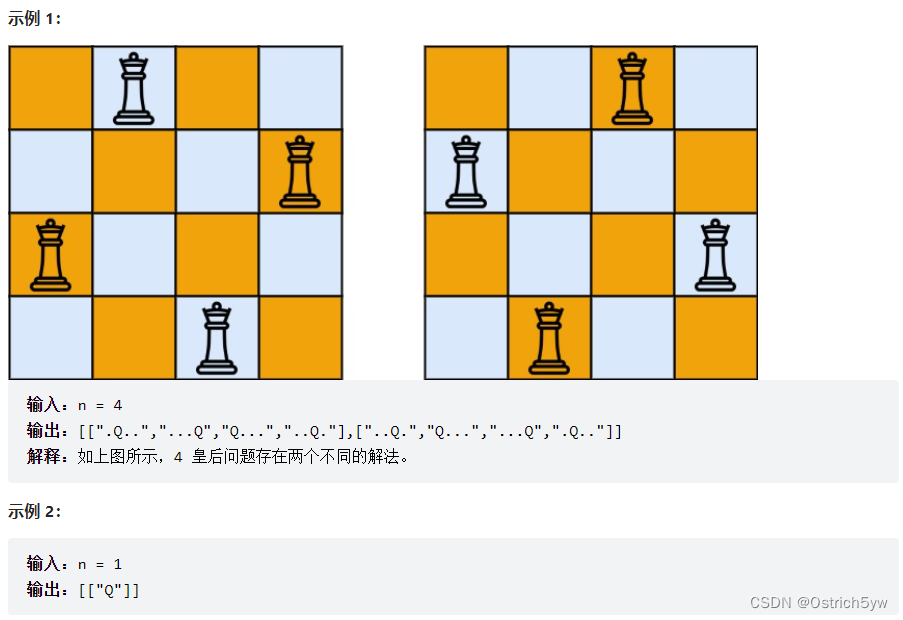
在这里插入图片描述

在这里插入图片描述

考察重点：需要找出所有情况，应立刻想到DFS，同时为了方便查找，使用二维数组代替链表进行遍历。使用isLegal()函数判断斜边，列是否存在Queen；DFS按行进行递归，每次在当前行，寻找合法的列插入Queen，并进入下一行。最终当递归到最后一行+1时，说明当前分布满足条件，加入结果链表list。

List<List<String>>  list;
public boolean isLegal(char map[][], int x, int y){for(int i = 0;i < map.length;i ++){if(map[i][y] != '.')return false;}for(int i = 1;i < map.length;i ++){if(x+i < map.length && y+i <map.length && map[x + i][y + i] != '.')return false;if(x-i >= 0 && y-i >= 0 && map[x - i][y - i] != '.')return false;if(x+i < map.length && y-i >= 0 && map[x + i][y - i] != '.')return false;if(x-i >= 0 && y+i < map.length && map[x - i][y + i] != '.')return false;}return true;
}
public int dfs(char[][] map, int x){if(!(x < map.length)){List<String> single = new ArrayList<>();for(int i = 0;i < map.length;i ++)single.add(String.valueOf(map[i]));list.add(single);return 0;}for(int y = 0;y < map.length;y ++){if(isLegal(map, x, y)) {map[x][y] = 'Q';dfs(map, x + 1);map[x][y] = '.';}}return 0;
}
public List<List<String>> solveNQueens(int n) {list = new ArrayList<>();char[][] map = new char[n][n];for(int i = 0;i < n;i ++)for(int j = 0;j < n;j ++)map[i][j] = '.';dfs(map, 0);return list;
}