289. 生命游戏

题目描述：
根据 百度百科 ， 生命游戏 ，简称为 生命 ，是英国数学家约翰·何顿·康威在 1970 年发明的细胞自动机。

给定一个包含 m × n 个格子的面板，每一个格子都可以看成是一个细胞。每个细胞都具有一个初始状态： 1 即为 活细胞 （live），或 0 即为 死细胞 （dead）。每个细胞与其八个相邻位置（水平，垂直，对角线）的细胞都遵循以下四条生存定律：

如果活细胞周围八个位置的活细胞数少于两个，则该位置活细胞死亡；
如果活细胞周围八个位置有两个或三个活细胞，则该位置活细胞仍然存活；
如果活细胞周围八个位置有超过三个活细胞，则该位置活细胞死亡；
如果死细胞周围正好有三个活细胞，则该位置死细胞复活；
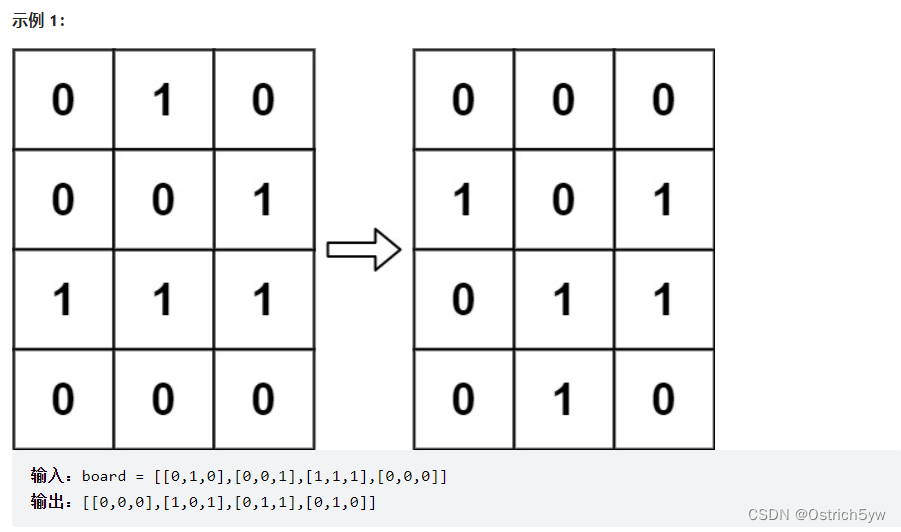
下一个状态是通过将上述规则同时应用于当前状态下的每个细胞所形成的，其中细胞的出生和死亡是同时发生的。给你 m x n 网格面板 board 的当前状态，返回下一个状态。
希望在原地数组解决问题

考察重点：在原矩阵基础上，原地将矩阵每个位置，根据该点周围8个点的原矩阵值转换为新值。使用way数组代替走的方向，从上至下从左至右依次遍历。oneNum记录活细胞个数，board[x][y]=2记录本轮复活的元素，3记录本轮死亡的元素；在递归完成，回溯的时候，再将二者转化为0，1。

var way [][]int = [][]int{{0, 1}, {0, -1}, {1, 0}, {-1, 0}, {1, 1}, {1, -1}, {-1, 1}, {-1, -1}}func dfs(board [][]int, x, y int) {oneNum := 0xLen, yLen := len(board), len(board[0])if y >= yLen {if x < xLen-1 {x, y = x+1, 0} else {return}}for i := 0; i < len(way); i++ {tempx := x + way[i][0]tempy := y + way[i][1]if tempx >= xLen || tempx < 0 || tempy >= yLen || tempy < 0 {continue}switch board[tempx][tempy] {case 1:oneNum++case 2:continuecase 0:continuecase 3:oneNum++}}if board[x][y] == 1 {if oneNum < 2 {board[x][y] = 3} else if oneNum <= 3 {board[x][y] = 1} else {board[x][y] = 3}} else {if oneNum == 3 {board[x][y] = 2} else {board[x][y] = 0}}dfs(board, x, y+1)if board[x][y] == 3{board[x][y] = 0}else if board[x][y] == 2{board[x][y] = 1}
}
func gameOfLife(board [][]int) {dfs(board, 0, 0)
}