目录
- 使用高通滤波器锐化图像
- 由低通滤波器得到理想、高斯和巴特沃斯高通滤波器
- 指纹增强
- 频域中的拉普拉斯
- 钝化掩蔽、高提升滤波和高频强调滤波
- 同态滤波
使用高通滤波器锐化图像
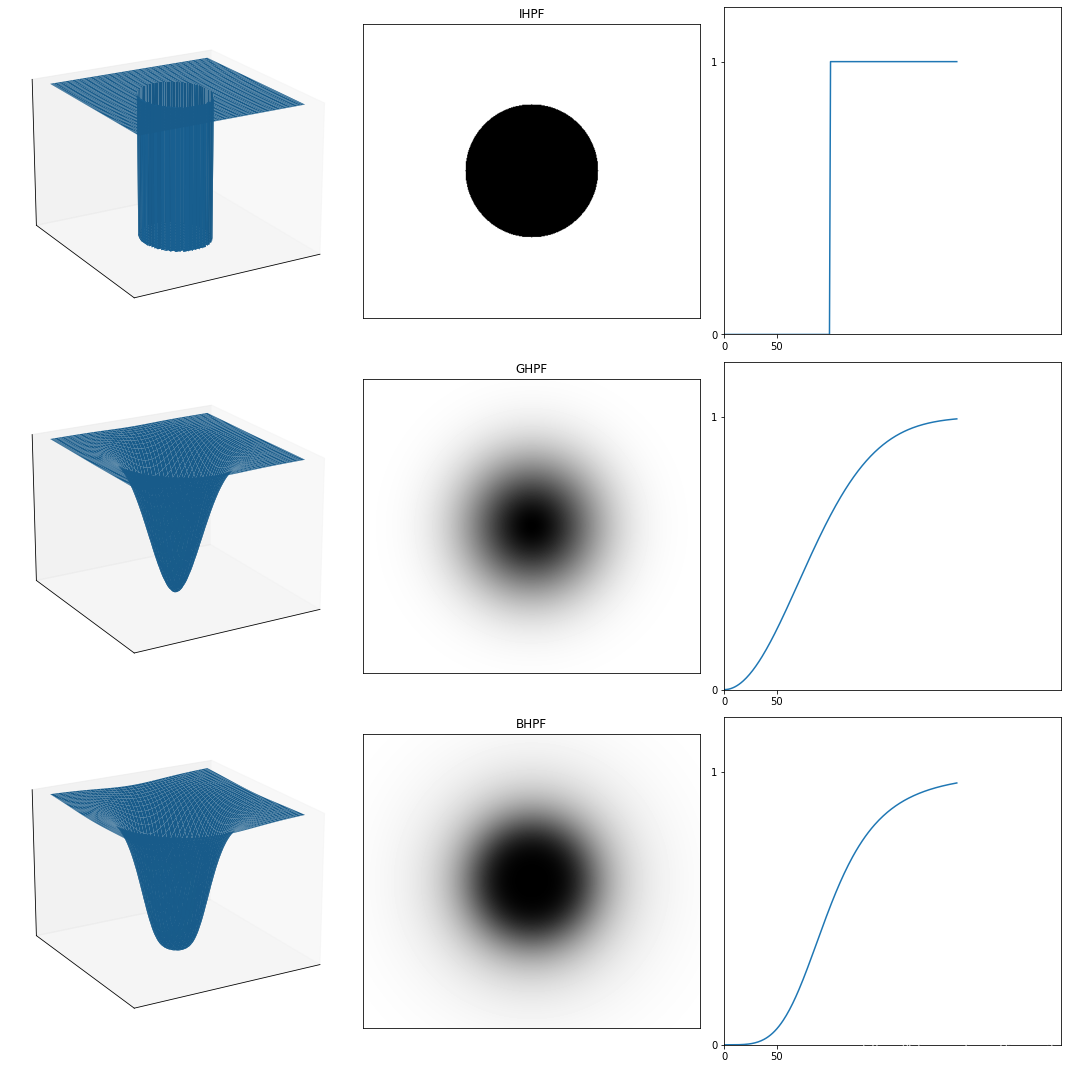
由低通滤波器得到理想、高斯和巴特沃斯高通滤波器
HHP(u,v)=1−HLP(u,v)(4.118)H_{HP}(u, v) = 1 - H_{LP}(u, v) \tag{4.118}HHP(u,v)=1−HLP(u,v)(4.118)
-
理想高通
H(u,v)={0,D(u,v)≤D01,D(u,v)>D0(4.119)H(u, v) = \begin{cases} 0, &D(u, v) \leq D_0 \\1, &D(u, v) > D_0\end{cases} \tag{4.119}H(u,v)={0,1,D(u,v)≤D0D(u,v)>D0(4.119) -
高斯高通
H(u,v)=1−e−D2(u,v)/2D02(4.120)H(u,v) = 1 - e^{-D^2(u,v) / 2D_0^2} \tag{4.120}H(u,v)=1−e−D2(u,v)/2D02(4.120) -
巴特沃斯高通
H(u,v)=11+[D0/D(u,v)]2n(4.121)H(u,v) = \frac{1} {1 + [D_0 / D(u,v)]^{2n}} \tag{4.121}H(u,v)=1+[D0/D(u,v)]2n1(4.121)
def idea_high_pass_filter(source, center, radius=5):"""create idea high pass filter param: source: input, source imageparam: center: input, the center of the filter, where is the lowest value, (0, 0) is top left corner, source.shape[:2] is center of the source imageparam: radius: input, the radius of the lowest value, greater value, bigger blocker out range, if the radius is 0, then allvalue is 0return a [0, 1] value filter"""M, N = source.shape[1], source.shape[0]u = np.arange(M)v = np.arange(N)u, v = np.meshgrid(u, v)D = np.sqrt((u - center[1]//2)**2 + (v - center[0]//2)**2)D0 = radiuskernel = D.copy()kernel[D > D0] = 1kernel[D <= D0] = 0return kernel
def gauss_high_pass_filter(source, center, radius=5):"""create gaussian high pass filter param: source: input, source imageparam: center: input, the center of the filter, where is the lowest value, (0, 0) is top left corner, source.shape[:2] is center of the source imageparam: radius: input, the radius of the lowest value, greater value, bigger blocker out range, if the radius is 0, then allvalue is 1return a [0, 1] value filter"""M, N = source.shape[1], source.shape[0]u = np.arange(M)v = np.arange(N)u, v = np.meshgrid(u, v)D = np.sqrt((u - center[1]//2)**2 + (v - center[0]//2)**2)D0 = radiusif D0 == 0:kernel = np.ones(source.shape[:2], dtype=np.float)else:kernel = 1 - np.exp(- (D**2)/(D0**2)) return kernel
def butterworth_high_pass_filter(img, center, radius=5, n=1):"""create butterworth high pass filter param: source: input, source imageparam: center: input, the center of the filter, where is the lowest value, (0, 0) is top left corner, source.shape[:2] is center of the source imageparam: radius: input, the radius of the lowest value, greater value, bigger blocker out range, if the radius is 0, then allvalue is 0param: n: input, float, the order of the filter, if n is small, then the BHPF will be close to GHPF, and more smooth from lowfrequency to high freqency.if n is large, will close to IHPFreturn a [0, 1] value filter""" epsilon = 1e-8M, N = img.shape[1], img.shape[0]u = np.arange(M)v = np.arange(N)u, v = np.meshgrid(u, v)D = np.sqrt((u - center[1]//2)**2 + (v - center[0]//2)**2)D0 = radiuskernel = (1 / (1 + (D0 / (D + epsilon))**(2*n)))return kernel
# 理想、高斯、巴特沃斯高通传递函数
from mpl_toolkits.mplot3d import Axes3D
import numpy as np
from matplotlib import pyplot as plt
from matplotlib import cmcenter = img_ori.shaperadius = 100
IHPF = idea_high_pass_filter(img_ori, img_ori.shape, radius=radius)
GHPF = gauss_high_pass_filter(img_ori, img_ori.shape, radius=radius)
BHPF = butterworth_high_pass_filter(img_ori, img_ori.shape, radius=radius, n=2)filters = ['IHPF', 'GHPF', 'BHPF']
# 用来绘制3D图
M, N = img_ori.shape[1], img_ori.shape[0]
u = np.arange(M)
v = np.arange(N)
u, v = np.meshgrid(u, v)fig = plt.figure(figsize=(15, 15))for i in range(len(filters)):ax_1 = fig.add_subplot(3, 3, i*3 + 1, projection='3d')plot_3d(ax_1, u, v, eval(filters[i]))ax_2 = fig.add_subplot(3, 3, i*3 + 2)ax_2.imshow(eval(filters[i]),'gray'), ax_2.set_title(filters[i]), ax_2.set_xticks([]), ax_2.set_yticks([])h_1 = eval(filters[i])[img_ori.shape[0]//2:, img_ori.shape[1]//2]ax_3 = fig.add_subplot(3, 3, i*3 + 3)ax_3.plot(h_1), ax_3.set_xticks([0, radius//2]), ax_3.set_yticks([0, 1]), ax_3.set_xlim([0, 320]), ax_3.set_ylim([0, 1.2])
plt.tight_layout()
plt.show()
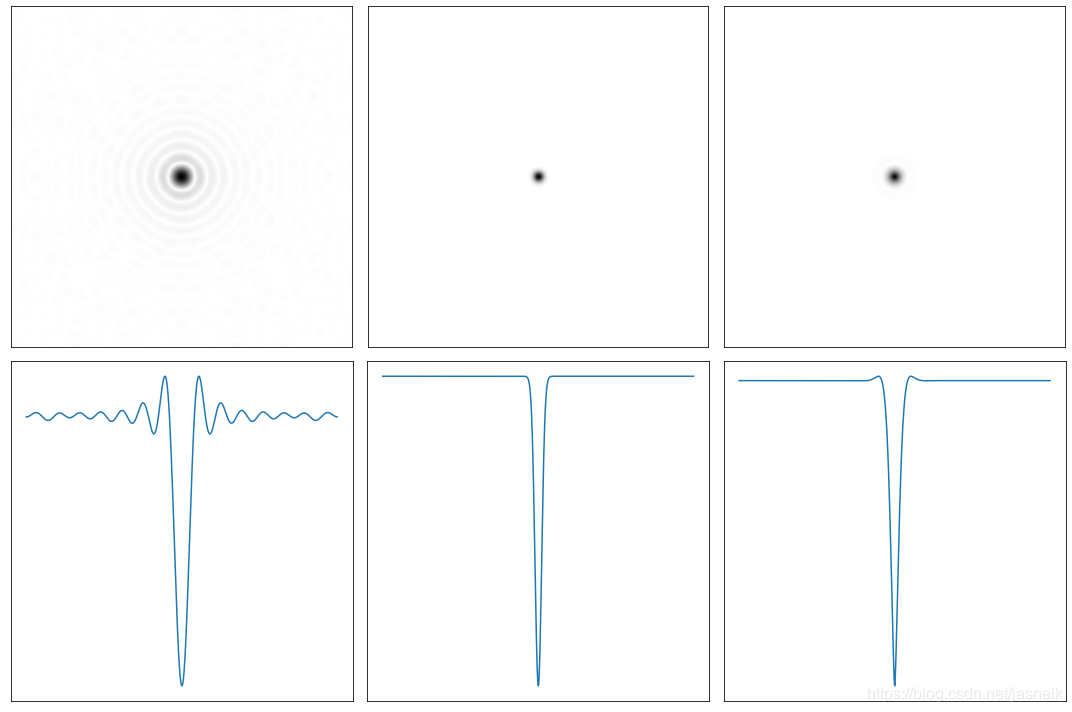
# 频率域理想、高通、巴特沃斯高通滤波器传递函数对应的空间核函数
# 这里简单用1 - 低通滤波器而生成
img_temp = np.zeros([1000, 1000])radius = 15
# IHPF = idea_high_pass_filter(img_temp, img_temp.shape, radius=radius)
# GHPF = gauss_high_pass_filter(img_temp, img_temp.shape, radius=radius)
# BHPF = butterworth_high_pass_filter(img_temp, img_temp.shape, radius=radius, n=2)
# filters = ['IHPF', 'GHPF', 'BHPF']ILPF = idea_low_pass_filter(img_temp, img_temp.shape, radius=radius)
GLPF = gauss_low_pass_filter(img_temp, img_temp.shape, radius=radius)
BLPF = butterworth_low_pass_filter(img_temp, img_temp.shape, radius=radius, n=2)
filters = ['ILPF', 'GLPF', 'BLPF']fig = plt.figure(figsize=(15, 10))
for i in range(len(filters)):# 这是显示空间域的核ax = fig.add_subplot(2, 3, i+1)spatial, spatial_s = frequen2spatial(eval(filters[i]))ax.imshow(1 - spatial_s, 'gray'), ax.set_xticks([]), ax.set_yticks([])# 这里显示是对应的空间域核水平扫描线的灰度分布ax = fig.add_subplot(2, 3, i+4)hx = spatial[:, 500]hx = centralized_2d(hx.reshape(1, -1)).flatten()ax.plot(1 - hx), ax.set_xticks([]), ax.set_yticks([])
plt.tight_layout()
plt.show()
def hpf_test(img_ori, mode='constant', radius=10, **params):"""param: img_ori: input imageparam: mode: input, str, is numpy pad parameter, default is 'constant'. for more detail please refere to Numpy padparam: **params: can accept multiply parameters, params['filter'] to choose which filter to use, if filter='butterworth', will need n=1 following, value varyparam: radius: the cut-off frequency size, default is 10return image with negetive and positive value, you might need to normalize the image or clip the value to certain value to show"""M, N = img_ori.shape[:2]# 填充fp = pad_image(img_ori, mode=mode)# 中心化fp_cen = centralized_2d(fp)# 正变换fft = np.fft.fft2(fp_cen)# 滤波器if params['filter'] == "gauss":H = gauss_high_pass_filter(fp, center=fp.shape, radius=radius)elif params['filter'] == "idea":H = idea_high_pass_filter(fp, center=fp.shape, radius=radius)elif params['filter'] == "butterworth":H = butterworth_high_pass_filter(fp, center=fp.shape, radius=radius, n = params['n'])# 滤波HF = fft * H# 反变换ifft = np.fft.ifft2(HF)# 去中心化gp = centralized_2d(ifft.real)# 还回来与原图像的大小g = gp[:M, :N]# 把负值截断
# g = np.clip(g, 0, g.max())dst = g
# dst = np.uint8(normalize(g) * 255)return dst
# 理想、高斯、巴特沃斯高通滤波器字符测试模式
# 图像具有负值与正值,这里把负值都置为0
img_ori = cv2.imread('DIP_Figures/DIP3E_Original_Images_CH04/Fig0448(a)(characters_test_pattern).tif', -1)
radius = [60, 160]
filters = ['idea', 'gauss', 'butterworth']
fig = plt.figure(figsize=(17, 10))
for i in range(len(radius)):for j in range(len(filters)):ax = fig.add_subplot(2, 3, 3*i+j+1)if filters[j] == 'butterworth':img = hpf_test(img_ori, mode='reflect', radius=radius[i], filter=filters[j], n=2)else:img = hpf_test(img_ori, mode='reflect', radius=radius[i], filter=filters[j])img = np.clip(img, 0, img.max())ax.imshow(img, 'gray', vmin=0, vmax=255), ax.set_xticks([]), ax.set_yticks([])ax.set_title("radius = " + str(radius[i])+ ' , ' + filters[j])
plt.tight_layout()
plt.show()

# 理想、高斯、巴特沃斯高通滤波器字符测试模式
# 图像具有负值与正值,这里把图像重新标定显示
img_ori = cv2.imread('DIP_Figures/DIP3E_Original_Images_CH04/Fig0448(a)(characters_test_pattern).tif', -1)
radius = [160]
filters = ['idea', 'gauss', 'butterworth']
fig = plt.figure(figsize=(17, 10))
for i in range(len(radius)):for j in range(len(filters)):ax = fig.add_subplot(2, 3, 3*i+j+1)img = hpf_test(img_ori, filters[j], mode='reflect', radius=radius[i])img = np.uint8(normalize(img) * 255)ax.imshow(img, 'gray'), ax.set_xticks([]), ax.set_yticks([])ax.set_title("radius = " + str(radius[i])+ ' , ' + filters[j])
plt.tight_layout()
plt.show()

从上面的图形可以看到,高通滤波器在边缘和边界的检测非常重要。
但理想高通滤波器出现了振铃效应。
# 频率域滤波过程
img_ori = cv2.imread('DIP_Figures/DIP3E_Original_Images_CH04/Fig0448(a)(characters_test_pattern).tif', -1)
M, N = img_ori.shape[:2]
fig = plt.figure(figsize=(15, 15))# 这里对原图像进行pad,以得到更好的显示
img_ori_show = np.ones([img_ori.shape[0]*2, img_ori.shape[1]*2]) * 255
img_ori_show[:img_ori.shape[0], img_ori.shape[1]:] = img_ori
ax_1 = fig.add_subplot(3, 3, 1)
imshow_img(img_ori_show, ax_1)fp = pad_image(img_ori, mode='constant')
ax_2 = fig.add_subplot(3, 3, 2)
imshow_img(fp, ax_2)fp_cen = centralized_2d(fp)
fp_cen_show = np.clip(fp_cen, 0, 255) # 负数的都截断为0
ax_3 = fig.add_subplot(3, 3, 3)
ax_3.imshow(fp_cen_show, cmap='gray'), ax_3.set_xticks([]), ax_3.set_yticks([])fft = np.fft.fft2(fp_cen)
spectrum = spectrum_fft(fft)
spectrum = np.log(1 + spectrum)
ax_4 = fig.add_subplot(3, 3, 4)
imshow_img(spectrum, ax_4)H = gauss_high_pass_filter(fp, center=fp.shape, radius=300)
ax_5 = fig.add_subplot(3, 3, 5)
imshow_img(H, ax_5)HF = fft * H
HF_spectrum = np.log(1 + spectrum_fft(HF))
ax_6 = fig.add_subplot(3, 3, 6)
imshow_img(HF_spectrum, ax_6)ifft = np.fft.ifft2(HF)
gp = centralized_2d(ifft.real)
ax_7 = fig.add_subplot(3, 3, 7)
imshow_img(gp, ax_7)# 最终结果有黑边
g = gp[:M, :N]
g = np.clip(g, 0, g.max())
ax_8 = fig.add_subplot(3, 3, 8)
imshow_img(g, ax_8)plt.tight_layout()
plt.show()

指纹增强
# 使用高能滤波和阈值处理增强图像
img_finger = cv2.imread('DIP_Figures/DIP3E_Original_Images_CH04/Fig0457(a)(thumb_print).tif', 0) #直接读为灰度图像
img_back = hpf_test(img_finger, mode='reflect', radius=50, filter='butterworth', n=4)
img_thres = np.clip(img_back, 0, 1)plt.figure(figsize=(24, 8))
plt.subplot(1, 3, 1),plt.imshow(img_finger,'gray'),plt.title('origial'), plt.xticks([]), plt.yticks([])
plt.subplot(1, 3, 2),plt.imshow(img_back,'gray'),plt.title('After GHPF'), plt.xticks([]), plt.yticks([])
plt.subplot(1, 3, 3),plt.imshow(img_thres,'gray'),plt.title('Threshold'), plt.xticks([]), plt.yticks([])
plt.tight_layout()
plt.show()

# 使用高能滤波和阈值处理增强图像
import cv2
import numpy as np
import matplotlib.pyplot as pltimg_finger = cv2.imread('DIP_Figures/DIP3E_Original_Images_CH04/Fig0457(a)(thumb_print).tif', 0) #直接读为灰度图像plt.figure(figsize=(15, 12))
plt.subplot(221),plt.imshow(img_finger,'gray'),plt.title('origial')#--------------------------------
fft = np.fft.fft2(img_finger)
fft_shift = np.fft.fftshift(fft)
amp_img = np.abs(np.log(1 + np.abs(fft_shift)))
plt.subplot(222),plt.imshow(amp_img,'gray'),plt.title('FFT')#--------------------------------
BHPF = butterworth_high_pass_filter(img_finger, img_finger.shape, radius=30, n=4)
plt.subplot(223),plt.imshow(BHPF,'gray'),plt.title('BHPF')#--------------------------------
f1shift = fft_shift * BHPF
f2shift = np.fft.ifftshift(f1shift) #对新的进行平移
img_back = np.fft.ifft2(f2shift)#出来的是复数,无法显示
img_new = np.abs(img_back)#调整大小范围便于显示
img_new = (img_new-np.amin(img_new))/(np.amax(img_new)-np.amin(img_new))
plt.subplot(224),plt.imshow(img_new,'gray'),plt.title('After BHPF')plt.tight_layout()
plt.show()
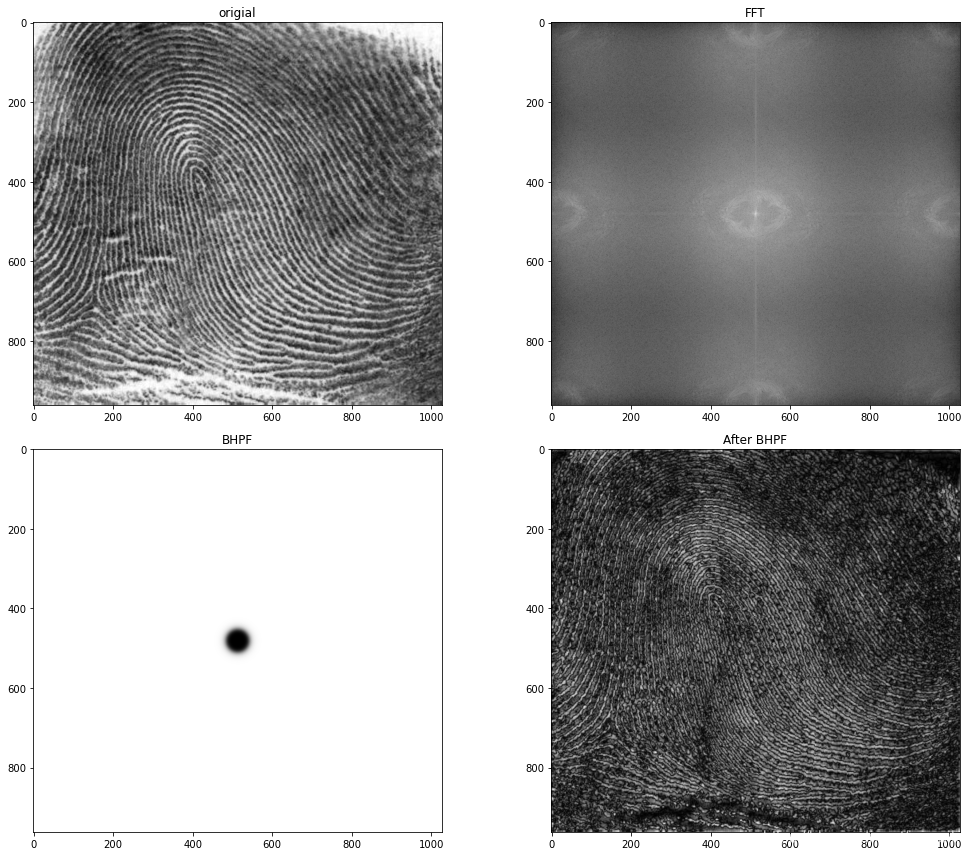
#调整大小范围便于显示
plt.figure(figsize=(15, 10))plt.subplot(121),plt.imshow(img_finger,'gray'),plt.title('Original')img_back_thred = np.clip(img_back.real, 0, 1)plt.subplot(122),plt.imshow(np.abs(img_back_thred),'gray'),plt.title('Thredhold after BHPF')plt.tight_layout()
plt.show()

频域中的拉普拉斯
拉普拉斯可用如下滤波器传递函数在频率域中实现:
H(u,v)=−4π2(u2+v2)(4.123)H(u,v) = -4\pi^2 (u^2 + v^2) \tag{4.123}H(u,v)=−4π2(u2+v2)(4.123)
或者关于频率矩形的中心
H(u,v)=−4π2[(u−M/2)2+(v−N/2)2]=−4π2D2(u,v)(4.124)H(u,v) = -4\pi^2 [(u - M/2)^2 + (v-N/2)^2] = -4\pi^2 D^2(u,v) \tag{4.124}H(u,v)=−4π2[(u−M/2)2+(v−N/2)2]=−4π2D2(u,v)(4.124)
D(u,v)=[(u−M/2)2+(v−N/2)2]1/2D(u,v) = [(u - M/2)^2 + (v-N/2)^2]^{1/2}D(u,v)=[(u−M/2)2+(v−N/2)2]1/2
∇2f(x,y)=J−1[H(u,v)F(u,v)](4.125)\nabla^2 f(x, y) = \mathfrak{J}^{-1}[H(u, v)F(u, v)] \tag{4.125}∇2f(x,y)=J−1[H(u,v)F(u,v)](4.125)
g(x,y)=f(xy)+c∇2f(x,y)(4.126)g(x, y) = f(x y) + c\nabla^2 f(x, y) \tag{4.126}g(x,y)=f(xy)+c∇2f(x,y)(4.126)
其中,c=−1c=-1c=−1,因为H(u,v)H(u, v)H(u,v)是负的。
用式(4.125)计算∇2f(x,y)\nabla^2 f(x, y)∇2f(x,y),这个因子的幅度要比fff的最大值要大几个数量级,所以要将fff与∇2f(x,y)\nabla^2 f(x, y)∇2f(x,y)的差限定在可比的范围内。
- 方法:
- 计算f(x,y)f(x, y)f(x,y)的DFT之前将f(x,y)f(x, y)f(x,y)的值归一化到[0, 1]
- 并将∇2f(x,y)\nabla^2 f(x, y)∇2f(x,y)除以它的最大值,进行限定在近似区间[-1, 1]。
g(x,y)=J−1{F(u,v)−H(u,v)F(u,v)}=J−1{[1−H(u,v)]F(u,v)}=J−1{[1+4π2D2]F(u,v)}(4.127)\begin{aligned} g(x, y) & = \mathfrak{J}^{-1}\big\{ F(u, v) - H(u, v)F(u, v) \big\} \\ & = \mathfrak{J}^{-1}\big\{ [1 - H(u, v)]F(u, v) \big\} = \mathfrak{J}^{-1}\big\{ [1 + 4\pi^2 D^2]F(u, v) \big\} \end{aligned}\tag{4.127}g(x,y)=J−1{F(u,v)−H(u,v)F(u,v)}=J−1{[1−H(u,v)]F(u,v)}=J−1{[1+4π2D2]F(u,v)}(4.127)
所以一般用式(4.125)公式先计算滤波后的结果,再进行处理。
def lapalacian_filter(source):"""这效果跟原来的不一样,有特改进"""M, N = source.shape[1], source.shape[0]u = np.arange(M)v = np.arange(N)u, v = np.meshgrid(u, v)D = np.sqrt((u - M//2)**2 + (v - N//2)**2)kernel = -4 * (np.pi**2 ) * (D**2)kernel_normal = kernel # (kernel - kernel.min()) / (kernel.max() - kernel.min())return kernel_normal
# 频域中的拉普拉斯滤波过程
img_ori = cv2.imread('DIP_Figures/DIP3E_Original_Images_CH04/Fig0458(a)(blurry_moon).tif', -1)
img_norm = img_ori / 255
M, N = img_ori.shape[:2]
fp = pad_image(img_norm, mode='constant')
fp_cen = centralized_2d(fp)
fft = np.fft.fft2(fp_cen)
H = lapalacian_filter(fp)
HF = fft * H
ifft = np.fft.ifft2(HF)
gp = centralized_2d(ifft.real)
g = gp[:M, :N]# 标定因子
g1 = g / g.max()
# 归一化
img = img_ori / 255.
# 根据公式进行增强
img_res = img - g1
img_res = np.clip(img_res, 0, 1)plt.figure(figsize=(13, 8))
plt.subplot(1,2, 1), plt.imshow(img,'gray'),plt.title('ORI'), plt.xticks([]), plt.yticks([])
plt.subplot(1,2, 2), plt.imshow(img_res,'gray'),plt.title('Transform'), plt.xticks([]), plt.yticks([])
plt.tight_layout()
plt.show()

钝化掩蔽、高提升滤波和高频强调滤波
gmask(x,y)=f(x,y)−fLP(x,y)(4.128)g_{mask}(x, y) = f(x, y) - f_{LP}(x,y) \tag{4.128}gmask(x,y)=f(x,y)−fLP(x,y)(4.128)
fLP(x,y)=J−1[HLP(u,v)F(u,v)](4.129)f_{LP}(x,y) = \mathfrak{J}^{-1} \big[ H_{LP}(u, v) F(u, v) \big] \tag{4.129}fLP(x,y)=J−1[HLP(u,v)F(u,v)](4.129)
g(x,y)=f(x,y)+kgmask(x,y)(3.56)g(x,y) = f(x,y) + k g_{mask}(x, y) \tag{3.56}g(x,y)=f(x,y)+kgmask(x,y)(3.56)
权值k≥0k \ge 0k≥0,k=1k = 1k=1时,它是钝化掩蔽,k>1k > 1k>1时,这个过程称为高提升滤波,选择k≤1k \leq 1k≤1可以减少钝化模板的贡献。
g(x,y)=J−1{[1+k[1−HLP(u,v)]]F(u,v)}(4.131)g(x,y) = \mathfrak{J}^{-1} \Big\{\big[1 + k[1 - H_{LP}(u, v)]\big] F(u, v) \Big\} \tag{4.131}g(x,y)=J−1{[1+k[1−HLP(u,v)]]F(u,v)}(4.131)
g(x,y)=J−1{[1+kHHP(u,v)]F(u,v)}(4.132)g(x,y) = \mathfrak{J}^{-1} \Big\{\big[1 + kH_{HP}(u, v)\big] F(u, v) \Big\} \tag{4.132}g(x,y)=J−1{[1+kHHP(u,v)]F(u,v)}(4.132)
[1+kHHP(u,v)]\big[1 + kH_{HP}(u, v)\big][1+kHHP(u,v)]称为高频强调滤波器传递函数。
- 高频强调滤波
g(x,y)=J−1{[k1+k2HHP(u,v)]F(u,v)}(4.133)g(x,y) = \mathfrak{J}^{-1} \Big\{\big[k_1 + k_2H_{HP}(u, v)\big] F(u, v) \Big\} \tag{4.133}g(x,y)=J−1{[k1+k2HHP(u,v)]F(u,v)}(4.133)
k1≥0k_1 \ge 0k1≥0偏移传递函数的值,以便使直流项不为零,而k2≥0k_2 \ge 0k2≥0控制高频的贡献
def frequency_filter(fshift, h):"""Frequency domain filtering using FFTparam: fshift: input, FFT shift to centerparam: h: input, filter, value range [0, 1]return an unnormalized reconstruct image, value may have negative and positive value"""# 滤波res = fshift * h# 反变换ifft = np.fft.ifft2(res)# 取实数部分gp = centralized_2d(ifft.real)return gp
def cdf_interp(img):"""global histogram equalization used numpy"""hist, bins = np.histogram(img, bins=256)cdf = hist.cumsum()cdf = 255 * cdf / cdf[-1] # 这个方法好像合理点,灰度值会比较小img_dst = np.interp(img.flatten(), bins[:-1], cdf)img_dst = np.uint8(img_dst.reshape(img.shape))return img_dst
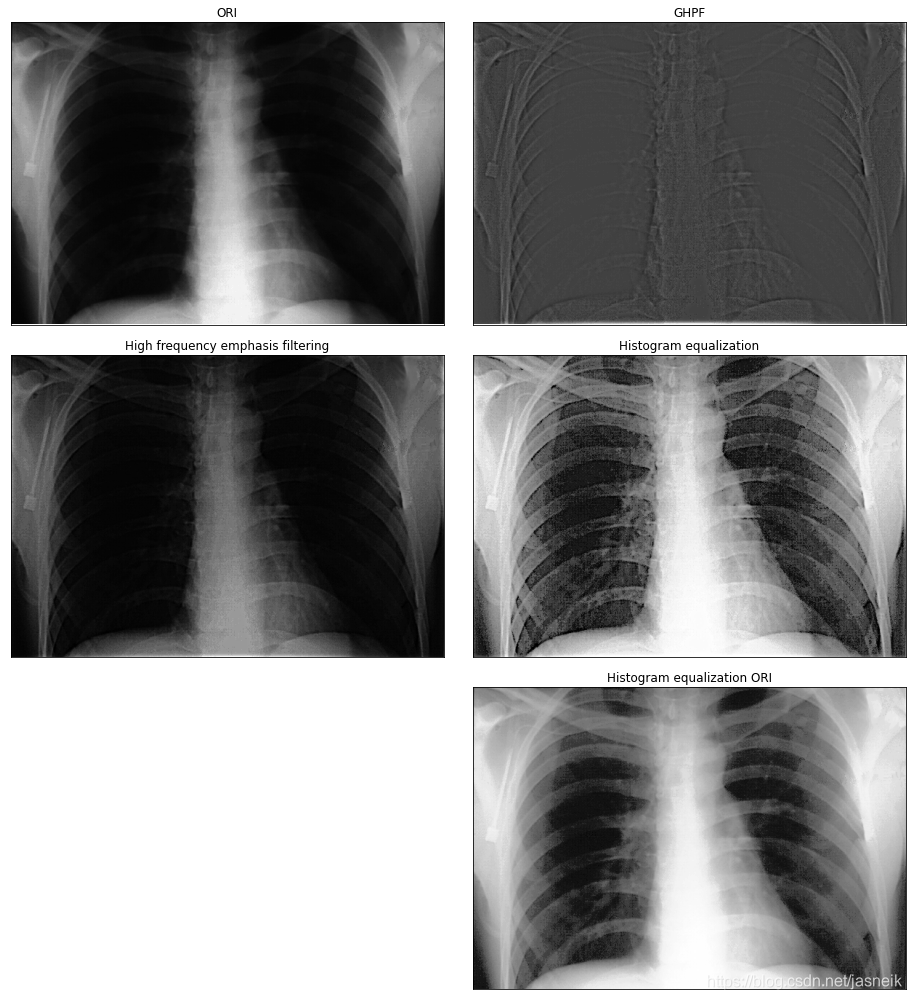
# 高频强调滤波 + 直方图均衡化
# 从图像来看,确实优于单独使用其中一种方法得到的结果,但直接对原图进行直方图均衡化,也能得到不错的结果。
img_ori = cv2.imread('DIP_Figures/DIP3E_Original_Images_CH04/Fig0459(a)(orig_chest_xray).tif', -1)
M, N = img_ori.shape[:2]# 填充
fp = pad_image(img_ori, mode='constant')
fp_cen = centralized_2d(fp)
fft = np.fft.fft2(fp_cen)# 滤波器
GHPF = gauss_high_pass_filter(fp, fp.shape, radius=70)
# 滤波后的图像
img_new = frequency_filter(fft, GHPF)
img_new = img_new[:M, :N]#=======高频增强滤波===================
k_1 = 0.5
k_2 = 0.75
res = fft * (k_1 + k_2 * GHPF)# 反变换
ifft = np.fft.ifft2(res)# 取实数部分
gp = centralized_2d(ifft.real)
g = gp[:M, :N]
g = np.clip(g, 0, g.max())temp = np.uint8(normalize(g) * 255)
img_res = cdf_interp(temp)hist_ori = cdf_interp(img_ori)plt.figure(figsize=(13, 14))
plt.subplot(3, 2, 1), plt.imshow(img_ori,'gray'),plt.title('ORI'), plt.xticks([]), plt.yticks([])
plt.subplot(3, 2, 2), plt.imshow(img_new,'gray'),plt.title('GHPF'), plt.xticks([]), plt.yticks([])
plt.subplot(3, 2, 3), plt.imshow(g,'gray'),plt.title('High frequency emphasis filtering'), plt.xticks([]), plt.yticks([])
plt.subplot(3, 2, 4), plt.imshow(img_res,'gray'),plt.title('Histogram equalization'), plt.xticks([]), plt.yticks([])
plt.subplot(3, 2, 6), plt.imshow(hist_ori,'gray'),plt.title('Histogram equalization ORI'), plt.xticks([]), plt.yticks([])
plt.tight_layout()
plt.show()
同态滤波
照射-反射模型可以赶通告个频率域程序,这个程序通过灰度范围压缩和对比度增强来同时改善图像的外观。图像f(x,y)f(x, y)f(x,y)可以表示为其照射分量i(x,y)i(x, y)i(x,y)和反射分量r(x,y)r(x, y)r(x,y):
f(x,y)=i(x,y)r(x,y)(4.134)f(x, y) = i(x, y) r(x, y) \tag{4.134}f(x,y)=i(x,y)r(x,y)(4.134)
因为乘积的傅里叶变换不是变换的乘积:
J[f(x,y)]≠J[i(x,y)]J[r(x,y)](4.135)\mathfrak{J}\big[f(x, y)\big] \neq \mathfrak{J}\big[i(x, y)\big] \mathfrak{J}\big[r(x, y)\big] \tag{4.135}J[f(x,y)]=J[i(x,y)]J[r(x,y)](4.135)
但我们可以自然对数变换得到:
J[z(x,y)]=J[lnf(x,y)]=J[lni(x,y)]J[lnr(x,y)](4.137)\mathfrak{J}\big[z(x, y)\big] = \mathfrak{J}\big[\text{ln}\;f(x, y)\big] = \mathfrak{J}\big[\text{ln}\; i(x, y)\big] \mathfrak{J}\big[\text{ln}\; r(x, y)\big] \tag{4.137}J[z(x,y)]=J[lnf(x,y)]=J[lni(x,y)]J[lnr(x,y)](4.137)
或者是
Z(u,v)=Fi(u,v)+Fr(u,v)(4.138)Z(u, v) = F_i(u, v) +F_r(u, v) \tag{4.138}Z(u,v)=Fi(u,v)+Fr(u,v)(4.138)
在频率域,可以用滤波器传递函数H(u,v)H(u, v)H(u,v)对Z(u,v)Z(u, v)Z(u,v)滤波,则有
S(u,v)=H(u,v)Z(u,v)=H(u,v)Fi(u,v)+H(u,v)Fr(u,v)(4.139)S(u, v) = H(u, v)Z(u, v) = H(u, v)F_i(u, v) + H(u, v)F_r(u, v) \tag{4.139}S(u,v)=H(u,v)Z(u,v)=H(u,v)Fi(u,v)+H(u,v)Fr(u,v)(4.139)
空间域中滤波后的图像是:
s(x,y)=J−1[S(u,v)]=J−1[H(u,v)Fi(u,v)]+J−1[H(u,v)Fr(u,v)](4.140)s(x, y) = \mathfrak{J}^{-1}[S(u, v)] = \mathfrak{J}^{-1}[H(u, v)F_i(u, v)] + \mathfrak{J}^{-1}[H(u, v)F_r(u, v)] \tag{4.140}s(x,y)=J−1[S(u,v)]=J−1[H(u,v)Fi(u,v)]+J−1[H(u,v)Fr(u,v)](4.140)
所以有
i′(x,y)=J−1[H(u,v)Fi(u,v)](4.141)i'(x, y) = \mathfrak{J}^{-1}[H(u, v)F_i(u, v)] \tag{4.141}i′(x,y)=J−1[H(u,v)Fi(u,v)](4.141)
r′(x,y)=J−1[H(u,v)Fr(u,v)](4.142)r'(x, y) = \mathfrak{J}^{-1}[H(u, v)F_r(u, v)] \tag{4.142}r′(x,y)=J−1[H(u,v)Fr(u,v)](4.142)
⇒\Rightarrow⇒
s(x,y)=i′(x,y)+r′(x,y)(4.143)s(x, y) = i'(x, y) + r'(x, y) \tag{4.143}s(x,y)=i′(x,y)+r′(x,y)(4.143)
因为z(x,y)z(x, y)z(x,y)是通过输入图像的自然对数形成的,所以可以通过取滤波后的结果的指数这一反处理来形成输出图像:
g(x,y)=es(x,y)=ei′(x,y)er′(x,y)(4.144)g(x, y) = e^{s(x, y)} = e^{i'(x, y)} e^{r'(x, y)} \tag{4.144}g(x,y)=es(x,y)=ei′(x,y)er′(x,y)(4.144)
这种方法是同态系统的一种特殊情况。可用同态滤波器传递函数H(u,v)H(u, v)H(u,v)分别对照射分量和反射分量进行操作。
图像的照射分量通常由慢空间变化来表征,而反射分量往往倾向于突变,特别是在不同目标的连接处。根据这此特征,我们可以将图像取对数后的傅里叶变换的低频与照射联系起来,而将高频与反射联系起来。尽管这些联系只是粗略的挖,但它们可以用于图像滤波。
- 同态滤波的步骤
f(x,y)⇒ln⇒DFT⇒H(u,v)⇒(DFT)−1⇒exp⇒g(x,y)f(x, y) \Rightarrow \text{ln} \Rightarrow \text{DFT} \Rightarrow H(u, v) \Rightarrow (\text{DFT})^{-1} \Rightarrow \text{exp} \Rightarrow g(x, y)f(x,y)⇒ln⇒DFT⇒H(u,v)⇒(DFT)−1⇒exp⇒g(x,y)
使用同态滤波器可更好的控制照射分量和反射分量。这种控制要求规定滤波器传递函数H(u,v)H(u, v)H(u,v),以便以不同的控制方法来影响傅里叶变换的低频和高频分量。
- 采用形式上稍有变化的GHPF函数可得到同态函数:
H(u,v)=(γH−γL)[1−e−cD2(u,v)/D02]+γL(4.147)H(u, v) = (\gamma_H - \gamma_L)\Big[1 - e^{-cD^2(u,v)/D_0^2}\Big] + \gamma_L \tag{4.147}H(u,v)=(γH−γL)[1−e−cD2(u,v)/D02]+γL(4.147)
若选择的γL\gamma_LγL和γH\gamma_HγH满足γL<1且γH≥1\gamma_L < 1且\gamma_H \ge 1γL<1且γH≥1,则滤波器函数将衰减低频(照射)的贡献,而放大高频(反射)的贡献。最终结果是同时进行动态范围的压缩和对比度的增强。
def gauss_homomorphic_filter(source, center, rl=0.5, rh=1, c=1, radius=5):"""create gaussian high pass filter param: source: input, source imageparam: center: input, the center of the filter, where is the lowest value, (0, 0) is top left corner, source.shape[:2] is center of the source imageparam: radius: input, the radius of the lowest value, greater value, bigger blocker out range, if the radius is 0, then allvalue is 1return a [rl, rh] value filter"""M, N = source.shape[1], source.shape[0]u = np.arange(M)v = np.arange(N)u, v = np.meshgrid(u, v)D = np.sqrt((u - center[1]//2)**2 + (v - center[0]//2)**2)D0 = radiuskernel = 1 - np.exp(- c * (D**2)/(D0**2)) kernel = (rh - rl) * kernel + rlreturn kernel
# 高斯同态滤波器与传递函数的径向剖面图
img_temp = np.zeros([1000, 1000])
GHF = gauss_homomorphic_filter(img_temp, img_temp.shape, rl=0.6, rh=1, c=0.4, radius=50)hx = GHF[500:, 500].flatten()fig = plt.figure(figsize=(15, 5))
ax_1 = fig.add_subplot(1, 2, 1)
ax_1.imshow(GHF, 'gray'), ax_1.set_xticks([]), ax_1.set_yticks([])ax_2 = fig.add_subplot(1, 2, 2)
ax_2.plot(hx), #ax_3.set_xticks([]), ax_3.set_yticks([])plt.tight_layout()
plt.show()
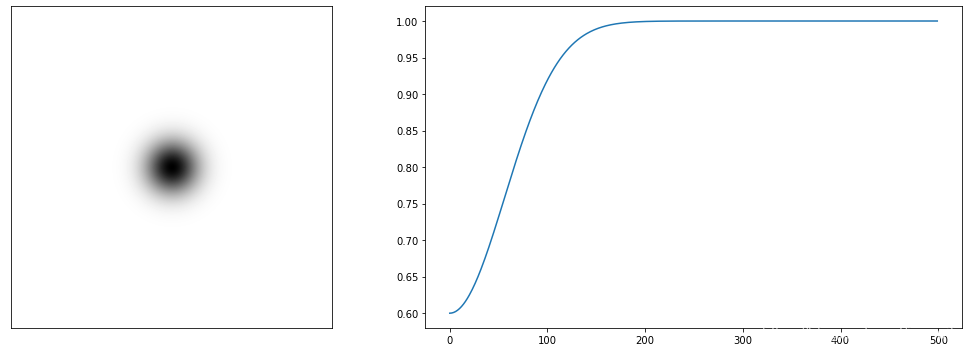
# 高斯同态滤波器
img_ori = cv2.imread('DIP_Figures/DIP3E_Original_Images_CH04/Fig0462(a)(PET_image).tif', -1)
M, N = img_ori.shape[:2]# 填充
fp = pad_image(img_ori, mode='constant')
fp_cen = centralized_2d(fp)
fft = np.fft.fft2(fp_cen)# 滤波器
GHF = gauss_homomorphic_filter(fp, fp.shape, rl=0.5, rh=3, c=5, radius=20)# 滤波后的图像
img_new = frequency_filter(fft, GHF)
img_new = img_new[:M, :N]
# print(img_new.min(), img_new.max())
img_res = np.uint8(normalize((img_new)) * 255)plt.figure(figsize=(13, 14))
plt.subplot(1, 2, 1), plt.imshow(img_ori,'gray'),plt.title('ORI'), plt.xticks([]), plt.yticks([])
plt.subplot(1, 2, 2), plt.imshow(img_res,'gray'),plt.title('G-Homomorphic'), plt.xticks([]), plt.yticks([])
plt.tight_layout()
plt.show()
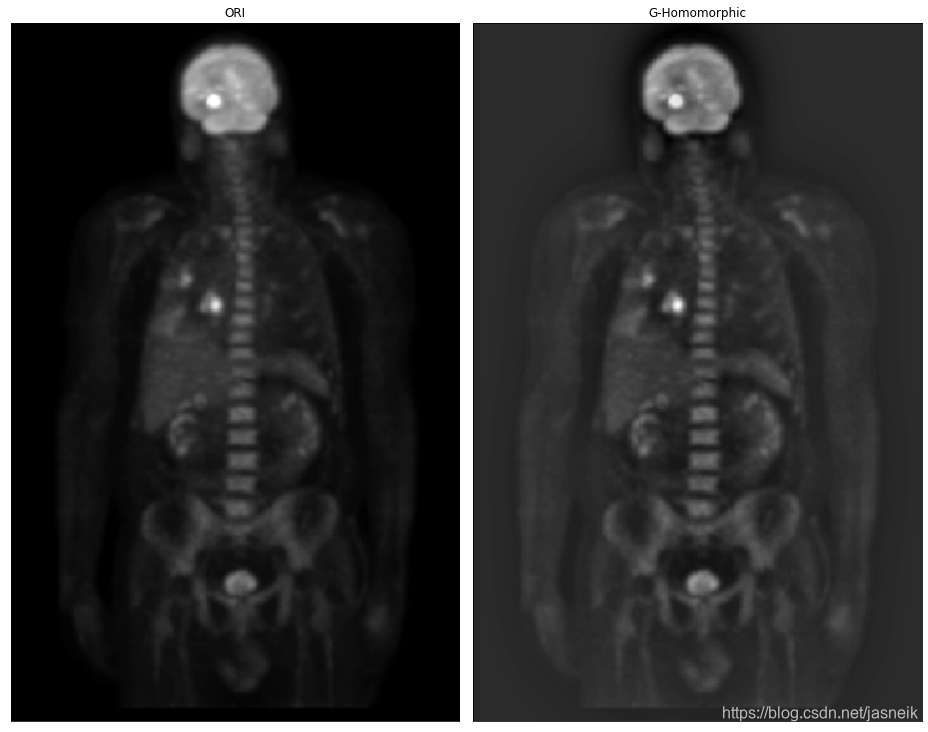
# 高斯同态滤波器,根据推导过程应用,但得到不好的图像,然后上面的直接应用的话,就算改变不同的参数,变化也不是很大
img_ori = cv2.imread('DIP_Figures/DIP3E_Original_Images_CH04/Fig0462(a)(PET_image).tif', -1)
M, N = img_ori.shape[:2]
img_ln = np.log(img_ori+1e-8)# 填充
fp = pad_image(img_ln, mode='constant')
fp_cen = centralized_2d(fp)
fft = np.fft.fft2(fp_cen)# 滤波器
GHF = gauss_homomorphic_filter(fp, fp.shape, rl=0.8, rh=1, c=3, radius=20)# 滤波后的图像
img_new = frequency_filter(fft, GHF)
img_new = img_new[:M, :N]
img_new = np.exp(img_new)img_new = np.clip(img_new, 0, img_new.max())
img_res = np.uint8(img_new / img_new.max() * 255)plt.figure(figsize=(13, 14))
plt.subplot(1, 2, 1), plt.imshow(img_ori,'gray'),plt.title('ORI'), plt.xticks([]), plt.yticks([])
plt.subplot(1, 2, 2), plt.imshow(img_new,'gray'),plt.title('G-Homomorphic'), plt.xticks([]), plt.yticks([])
plt.tight_layout()
plt.show()
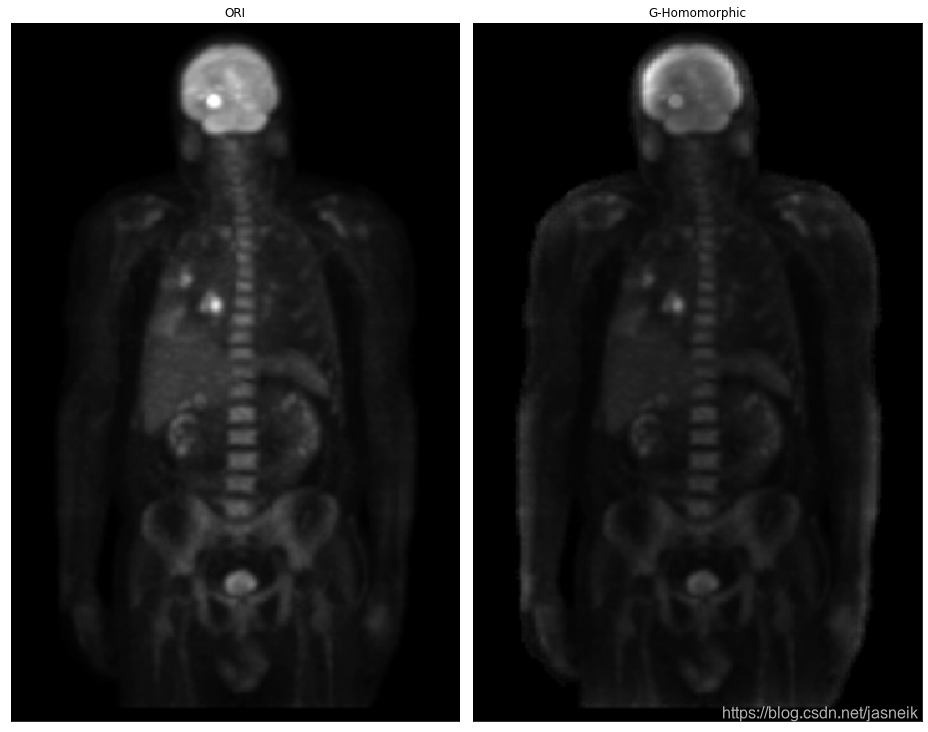



)

 - 频率域滤波12 - 选择性滤波 - 带阻)

![[物理学与PDEs]第1章第4节 电磁能量和电磁动量, 能量、动量守恒与转化定律 4.3 电磁能量 (动量) 密度, 电磁能量流 (动量流) 密度...](http://pic.xiahunao.cn/[物理学与PDEs]第1章第4节 电磁能量和电磁动量, 能量、动量守恒与转化定律 4.3 电磁能量 (动量) 密度, 电磁能量流 (动量流) 密度...)











