我们考虑SVM的对偶问题,我们通常是在对偶空间中进行求解的。
1、Lagrange Multipliers
对于一个很一般的问题
Minimize f(x)subject to {a(x)≥0b(x)≤0c(x)=0\begin{aligned} \text { Minimize } & f(x) \\ \text { subject to } \quad & \left\{\begin{array}{l} a(x) \geq 0 \\ b(x) \leq 0 \\ c(x)=0 \end{array}\right. \end{aligned} Minimize subject to f(x)⎩⎨⎧a(x)≥0b(x)≤0c(x)=0
构造拉氏函数
L(x,α)=f(x)−α1a(x)−α2b(x)−α3c(x){α1≥0α2≤0α3is unconstrained \begin{aligned} L(x, \alpha)= & f(x)-\alpha_1 a(x)-\alpha_2 b(x)-\alpha_3 c(x) \\ & \left\{\begin{array}{l} \alpha_1 \geq 0 \\ \alpha_2 \leq 0 \\ \alpha_3 \text { is unconstrained } \end{array}\right. \end{aligned} L(x,α)=f(x)−α1a(x)−α2b(x)−α3c(x)⎩⎨⎧α1≥0α2≤0α3 is unconstrained
我们对拉氏函数关于拉格朗日乘子求最大
maxαL(x,α)={f(x),if {a(x)≥0b(x)≤0c(x)=0+∞,otherwise \max _\alpha L(x, \alpha)=\left\{\begin{array}{lr} f(x), & \text { if }\left\{\begin{array}{l} a(x) \geq 0 \\ b(x) \leq 0 \\ c(x)=0 \end{array}\right. \\ +\infty, & \text { otherwise } \end{array}\right. αmaxL(x,α)=⎩⎨⎧f(x),+∞, if ⎩⎨⎧a(x)≥0b(x)≤0c(x)=0 otherwise
于是我们的优化目标变为
minxmaxαL(x,α)subject to {a(x)≥0b(x)≤0c(x)=0\begin{aligned} \min _x &\max _\alpha L(x, \alpha)\\ \text { subject to } \quad & \left\{\begin{array}{l} a(x) \geq 0 \\ b(x) \leq 0 \\ c(x)=0 \end{array}\right. \end{aligned} xmin subject to αmaxL(x,α)⎩⎨⎧a(x)≥0b(x)≤0c(x)=0
进一步的,我们又有
minxmaxαL(x,α)=maxαminxL(x,α)\min _x \max _\alpha L(x, \alpha)=\max _\alpha \min _x L(x, \alpha) xminαmaxL(x,α)=αmaxxminL(x,α)
当我们在内层把xxx消掉后,我们最终的优化问题将与样本无关,只与拉格朗日乘子有关,SVM似乎不会受样本的维数影响
2、KKT条件
Stationarity ∇f(x∗)−α1∇a(x∗)−α2∇b(x∗)−α3∇c(x∗)=0Primal feasibility {a(x∗)≥0b(x∗)≤0c(x∗)=0Dual feasibility {α1≥0α2≤0α3is unconstrained Complementary slackness {α1a(x∗)=0α2b(x∗)=0α3c(x∗)=0\begin{aligned} & \text { Stationarity } \nabla f\left(x^*\right)-\alpha_1 \nabla a\left(x^*\right)-\alpha_2 \nabla b\left(x^*\right)-\alpha_3 \nabla c\left(x^*\right)=0 \\ & \text { Primal feasibility }\left\{\begin{array}{l} a\left(x^*\right) \geq 0 \\ b\left(x^*\right) \leq 0 \\ c\left(x^*\right)=0 \end{array}\right. \\ & \text { Dual feasibility }\left\{\begin{array}{l} \alpha_1 \geq 0 \\ \alpha_2 \leq 0 \\ \alpha_3 \text { is unconstrained } \end{array}\right. \\ & \text { Complementary slackness }\left\{\begin{array}{l} \alpha_1 a\left(x^*\right)=0 \\ \alpha_2 b\left(x^*\right)=0 \\ \alpha_3 c\left(x^*\right)=0 \end{array}\right. \end{aligned} Stationarity ∇f(x∗)−α1∇a(x∗)−α2∇b(x∗)−α3∇c(x∗)=0 Primal feasibility ⎩⎨⎧a(x∗)≥0b(x∗)≤0c(x∗)=0 Dual feasibility ⎩⎨⎧α1≥0α2≤0α3 is unconstrained Complementary slackness ⎩⎨⎧α1a(x∗)=0α2b(x∗)=0α3c(x∗)=0
3、Hard Margin SVM 对偶问题
回到我们的Hard Margin SVM
Minimize 12∥w∥2\frac{1}{2}\|\mathbf{w}\|^221∥w∥2
subject to 1−yi(wTxi+b)≤01-y_i\left(\mathbf{w}^T \mathbf{x}_i+b\right) \leq 0 \quad1−yi(wTxi+b)≤0 for i=1,…,ni=1, \ldots, ni=1,…,n
构造拉格朗日函数
L=12wTw+∑i=1nαi(1−yi(wTxi+b))\mathcal{L}=\frac{1}{2} \mathbf{w}^T \mathbf{w}+\sum_{i=1}^n \alpha_i\left(1-y_i\left(\mathbf{w}^T \mathbf{x}_i+b\right)\right) L=21wTw+i=1∑nαi(1−yi(wTxi+b))
分别对权重和偏置求偏导
w+∑i=1nαi(−yi)xi=0⇒w=∑i=1nαiyixi∑i=1nαiyi=0αi≥0\begin{aligned} \mathbf{w}+\sum_{i=1}^n \alpha_i\left(-y_i\right) \mathbf{x}_i&=\mathbf{0} \quad \Rightarrow \quad \mathbf{w}=\sum_{i=1}^n \alpha_i y_i \mathbf{x}_i \\ \sum_{i=1}^n \alpha_i y_i&=0 \quad \alpha_i \geq 0 \\ & \end{aligned} w+i=1∑nαi(−yi)xii=1∑nαiyi=0⇒w=i=1∑nαiyixi=0αi≥0
因此将Hard Margin SVM转化为对偶问题(把求得的w\mathbf{w}w代入)
max.W(α)=∑i=1nαi−12∑i=1,j=1nαiαjyiyjxiTxjsubject to αi≥0,∑i=1nαiyi=0\begin{aligned} & \max . \quad W(\boldsymbol{\alpha})=\sum_{i=1}^n \alpha_i-\frac{1}{2} \sum_{i=1, j=1}^n \alpha_i \alpha_j y_i y_j \mathbf{x}_i^T \mathbf{x}_j \\ & \text { subject to } \alpha_i \geq 0, \sum_{i=1}^n \alpha_i y_i=0 \end{aligned} max.W(α)=i=1∑nαi−21i=1,j=1∑nαiαjyiyjxiTxj subject to αi≥0,i=1∑nαiyi=0
特别注意到:
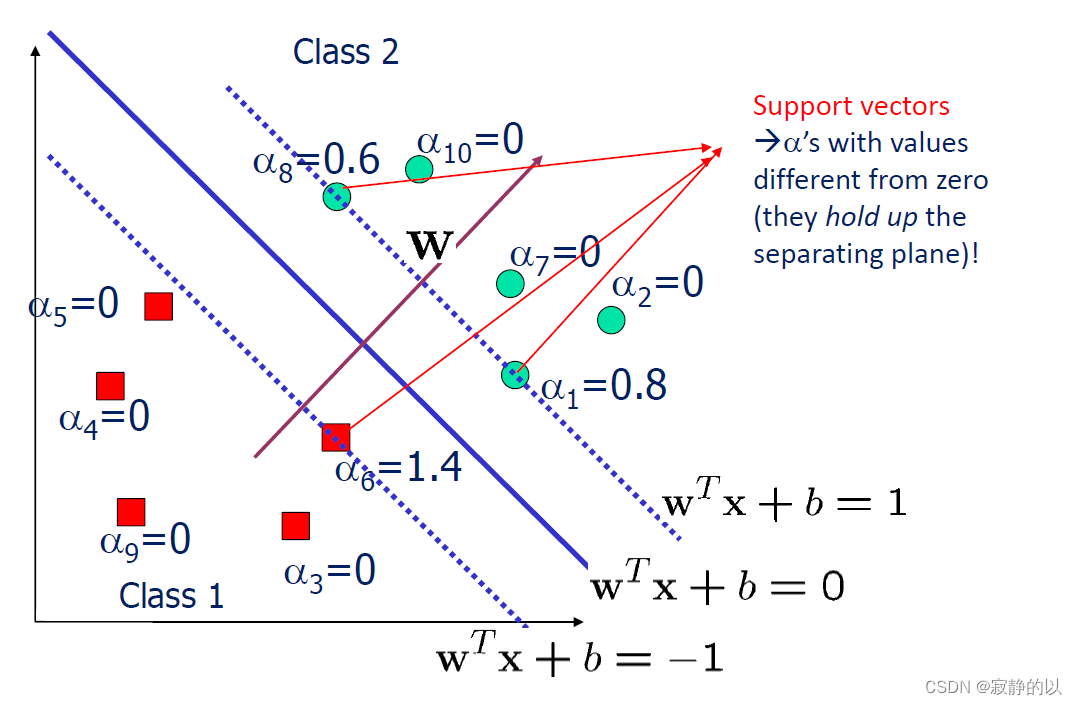
w=∑i=1nαiyixi\mathbf{w}=\sum_{i=1}^n \alpha_i y_i \mathbf{x}_i w=i=1∑nαiyixi
- 由于标签的值为+1或-1,所以上式隐含正负样本对分解面的贡献是大致相同的。正负样本规模大致相当
- 对于每一个样本xi\mathbf{x}_ixi,都有一个αi\alpha_iαi,而当αi\alpha_iαi为000时,该样本对分类器没有贡献,事实确实如此。而那些对分类器有贡献的样本又叫支撑向量Support Vectors
)







)



-- 配置文件之Gzip)






