目录
常见的三种排序方法
冒泡排序
插入排序
选择排序
其他经典的排序方法
快速排序
堆排序
归并排序
希尔排序
不同排序方法的各维度对比
排序方式的稳定性:若两个相同的元素在排序前后的相对位置不发生改变的排序为稳定排序,否则不稳定排序
常见的三种排序方法
以【3,2,2,1,1】为例
冒泡排序
冒泡排序思路:不断地对比相邻的两个元素,将若前面的元素 大于(注意不含等于) 后面的元素,则两个元素进行位置交换。
# 冒泡排序,复杂度为O(n^2)
def bubble_sorted(li:list)->list:for i in range(len(li)):# 第几趟exchanged = False# 这个是为了防止多余的遍历,如果前面的元素已经是排序好的,那就不需要再进行比较了,减少运行时间for j in range(len(li)-1):# 遍历列表元素if li[j] > li[j+1]:li[j],li[j+1] = li[j+1],li[j]exchanged = Trueif not exchanged:return li
第一趟
| 3 | 2(1) | 2(2) | 1(1) | 1(2) |
|---|---|---|---|---|
| 2(1) | 3 | 2(2) | 1(1) | 1(2) |
| 2(1) | 2(2) | 3 | 1(1) | 1(2) |
| 2(1) | 2(2) | 1(1) | 3 | 1(2) |
| 2(1) | 2(2) | 1(1) | 1(2) | 3 |
第二趟
第三趟
第四趟 、第五趟、第六趟
可见在经过冒泡排序后,相同元素的相对前后位置没有发生改变 ,因此排序是稳定的。
插入排序
插入排序的思路:从左到右,分为有序区和无序区,每次都是将无序区的第一个元素取出插入到有序区间中。然后从右往左遍历有序区,当遍历的有序元素大于该元素时,有序元素右移一位,继续遍历有序区;直到遍历的有序元素小于等于无序区元素第一个元素时,停止遍历,并且将该元素插入到停止遍历有序元素的后一个位置
# 插入排序,复杂度为O(n^2),思路是从左到右抽取一个元素,将这个元素,与左边邻近的元素比较,若比左边的小,则左边元素右移,
# 若不比左边的小了或者已经到最左边了,则将抽取的元素赋值给原本左边元素
def insert_sorted(li:list)->list:for i in range(1,len(li)):# 趟数,也就是抽牌的顺序,从第一张牌开始抽tmp = li[i]j = i - 1# 左边元素while j >= 0 and li[i] < li[j]:# 若抽取的元素小于邻近左边的元素,则将左边元素右移一格li[j+1] = li[j]j -= 1# 这时候的j已经不满足上述条件了,因此这个j位置上的元素没有移动,而j+1上位置的元素移动了是空的li[j+1] = tmpreturn li| 3 | 2(1) | 2(2) | 1(1) | 1(2) |
|---|---|---|---|---|
| 2(1) | 3 | 2(2) | 1(1) | 1(2) |
| 2(1) | 2(2) | 3 | 1(1) | 1(2) |
| 1(1) | 2(1) | 2(2) | 3 | 1(2) |
| 1(1) | 1(2) | 2(1) | 2(2) | 3 |
可见在经过插入排序后,相同元素的相对前后位置没有发生改变 ,因此排序是稳定的。
选择排序
选择排序的思路:分为有序区和无序区,每次将无序区的最小元素放在无序区的第一个位置,期间会发生元素的交换
# 选择排序,复杂度为O(n^2),思路是遍历一趟元素后,选择最小的值放在无序区的第一位
def select_sorted(li:list)->list:for i in range(len(li)):min_loc = i# 初始化最小值的位置为第一个for j in range(i+1,len(li)-1):if li[j]<li[min_loc]:li[j],li[min_loc] = li[min_loc],li[j]# 交换元素return li第一趟
| 3 | 2(1) | 2(2) | 1(1) | 1(2) |
|---|---|---|---|---|
| 2(1) | 3 | 2(2) | 1(1) | 1(2) |
| 2(1) | 3 | 2(2) | 1(1) | 1(2) |
| 1(1) | 3 | 2(2) | 2(1) | 1(2) |
。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。
在第一趟的选择排序种,我们可以看到相同元素2(1)和2(2)的相对位置在排序前后发生了变化,因此是不稳定排序。
其他经典的排序方法
快速排序
快排的思路:先取序列首元素作为基准值,将序列中小于基准值的元素放在左边,大于基准值的元素放在右边(相等的元素放在任一边均可)。然后以该基准值作为边界,对左右子序列递归进行快速排序即可实现排序
具体步骤:
1)选择序列首元素作为基准值,左指针指向序列首位,右指针指向序列尾部;
2)若右指针的元素值大于基准值,右指针继续左移;否则将右指针指向的元素赋值给左指针;
3)赋值完后,移动左指针,若左指针的元素小于基准值,左指针右移,否则将左指针指向的元素赋值给右指针处;
4)重复2)3)直到左右指针重合,将基准值赋值给重合的位置;
5)对左右子序列递归使用1)-4)步骤,这样就实现了对序列的快速排序,递归终止条件为序列含有1个元素,即left<right这里保证有两个元素的时候进行递归,否则退出
def partition(li:list,left:int,right:int)->int:'''这是根据路飞商城的思路来的将p元素归位的函数:取第一个元素为p元素,移动right,若right指针的值大于P,则right继续往左移动,否则停止移动,将值赋值给left所在的位置;然后再移动left,若left指针的值小于P,则left继续往右移动,否则停止移动,将值赋值给right所在的位置;如此交替移动,直到left=right时,停止,并将P值赋值给left(right):param li: 需要归位的列表:param left: 列表左指针索引,初始值为0:param right: 列表右指针索引,初始值为len(li)-1:return: 返回p归位的索引'''#得到要归位的元素(第一个元素)p = li[left]#当列表有两个元素时,才进行排序while left < right:# 保证有两个元素#这里我们从列表的右边开始进行元素的比较while left < right and p < li[right]: # 至少两个元素并且p元素值小于等于right指针指向的值时,右指针左移right -= 1 # right 左移一步li[left] = li[right] # 不满足上述循环条件时,停止移动right,并且将right上的值赋值给left#右指针停止移动后,开始进行左指针的移动while left < right and p > li[left]:left += 1li[right] = li[left]#当left = right时,说明已经归位了,将p赋值给归位位置li[left] = preturn leftdef quickSorted(li,left,right):'''对列表进行快排:param li: 需要排序的列表:param left: 左索引:param right: 右索引:return: 返回排好序的列表'''if left < right:mid = partition(li, left, right) # 首先得到第一个归位索引# 对左边列表进行排序quickSorted(li,left,mid-1)# 对右边列表进行排序quickSorted(li,mid + 1,right)第一趟
基准值p = 5
| 5 | 4(1) | 9 | 4(2) | 8 |
|---|---|---|---|---|
| 5 | 4(1) | 9 | 4(2) | 8 |
| 4(2) | 4(1) | 9 | 4(2) | 8 |
| 4(2) | 4(1) | 9 | 9 | 8 |
| 4(2) | 4(1) | 5 | 9 | 8 |
由上面可以看出,在进行一趟排序后,两个4的相对位置发生了改变,因此快速排序是不稳定的
。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。
堆排序
堆排序是利用了二叉树的数据结构来实现的,稳定排序
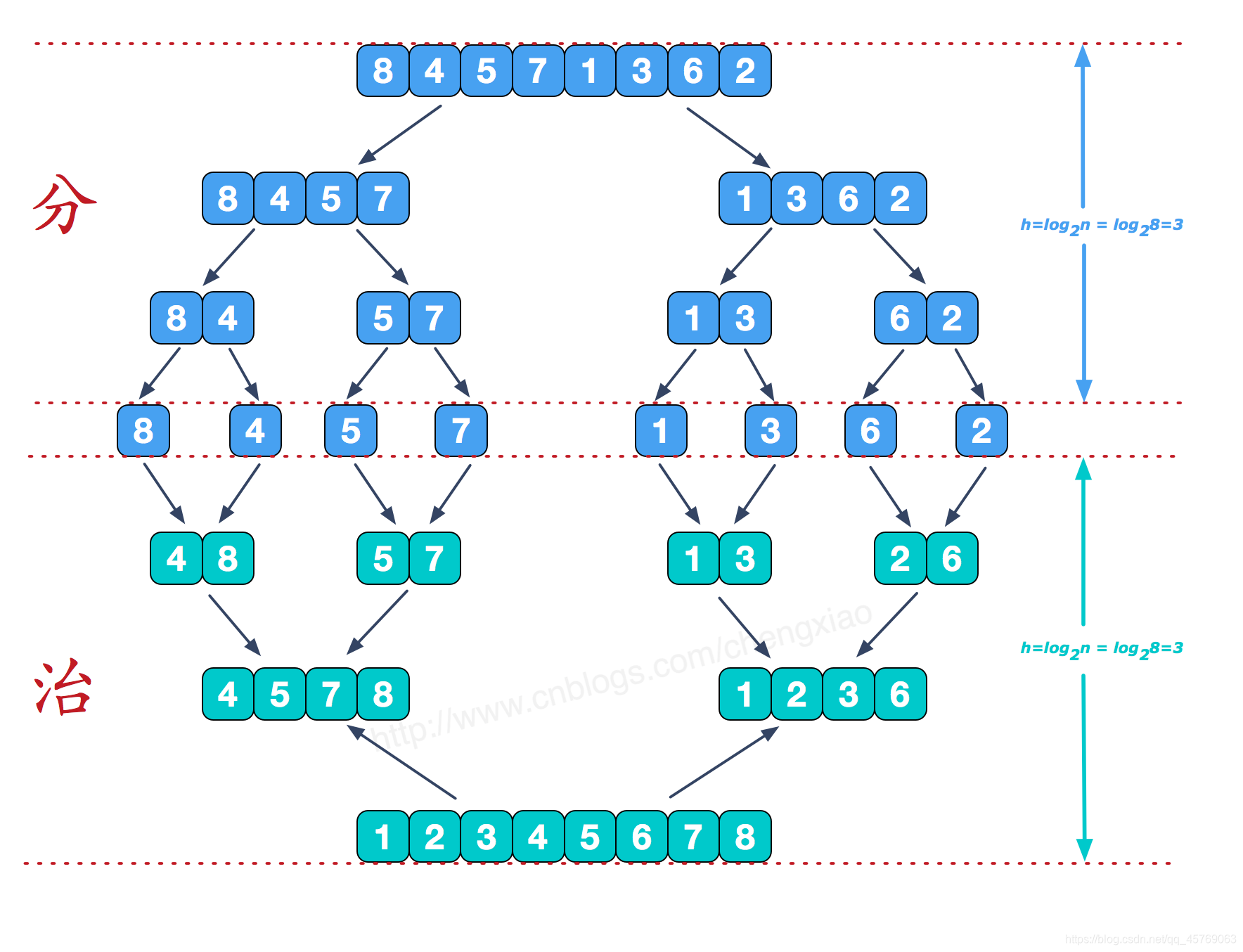
归并排序
归并排序的思路:将两个有序序列利用双指针进行合并
难点:如何将待排序的序列变成两个有序序列,当元素只有一个的时候序列是有序的,这个是比较容易理解的。因此这里利用递归的方式,先将列表拆成一个个单元素列表,然后再一个个元素(有序序列)合并,回溯即可实现排序
'''
归并排序的主要思路:将两个有序的子列表归并为一个有序的大列表
'''#归并函数,假设li是由左右两个有序的子列表组成,假设两个子列表都是从小到大排好序的列表
def merge(li,low,mid,high):''':param li: 由左右两个有序的子列表组成的大列表:param low: 列表的起始索引:param mid: 两个子列表的分解处的索引,这里取前面子列表的最后一个元素的索引为mid:param high: 大列表最后一个索引:return: 从小到大排序的列表'''# 当列表中有两个元素时进行归并操作i = low # 第一个子列表的起始索引j = mid + 1 # 第二个子列表的起始索引比较好了的元素lTmp = [] # 用于保存while i <= mid and j <= high: # 当两个子列表都没有遍历完时if li[i] > li[j]:lTmp.append(li[j])j += 1else:lTmp.append(li[i])i += 1while i <= mid:# 当右列表访问结束后,直接将左列表进行添加lTmp.append(li[i])i += 1while j <= high:lTmp.append(li[j])j += 1li[low:high+1] = lTmp#归并排序
def mergeSorted(li,low,high):''':param li: 列表:param low: 列表起始索引:param high: 列表结束索引:return: '''if low < high: # 保证列表有两个元素mid = (low + high)//2mergeSorted(li,low,mid) # 对左列表进行排序mergeSorted(li,mid+1,high) # 对右列表进行排序merge(li,low,mid,high) # 将排好序的两个列表进行归并归并排序是稳定排序方式,因为在进行有序列表的合并时,这里看成左右子序列的合并,只有当左序列中的元素大于右子序列的元素的时候,才会将右子序列的元素添加到列表中,这也就保证了在左右序列中有相等元素时,会先将左序列的元素存放在列表中,然后再将右序列的元素存放在列表中
希尔排序
希尔排序思路:希尔排序的思路其实和归并排序是类似的,都是利用分治的方法实现,不同的是归并排序是另开一个数组来合并两个有序的序列进而实现序列的排序;而希尔排序则是利用插入的方式将两个子序列合并在一起,在序列原地进行修改。
'''
希尔排序:将列表分成多组,对每一组进行插入排序,最后合并在一起,d1=len//2,di=d(i-1)//2,直到di=1,退出
'''def insert_sorted_shell(li:list,gap:int)->list:''':param li: 列表:param gap: 分组的组数和每个元素在大列表中的间隔:return: '''for i in range(gap,len(li)):# 趟数,也就是抽牌的顺序,从第一张牌开始抽tmp = li[i]j = i - gap# 左边元素while j >= 0 and li[i] < li[j]:# 若抽取的元素小于邻近左边的元素,则将左边元素右移一格li[j+gap] = li[j]j -= gap# 这时候的j已经不满足上述条件了,因此这个j位置上的元素没有移动,而j+1上位置的元素移动了是空的li[j+gap] = tmpreturn lidef shellSorted(li):n = len(li)d = n//2while d >= 1:insert_sorted_shell(li,d)d //= 2注意:快速排序、归并排序的左右索引都是闭区间
不同排序方法的各维度对比
| 排序方法 | 冒泡排序 | 插入排序 | 选择排序 | 快速排序 | 归并排序 | 希尔排序 |
|---|---|---|---|---|---|---|
| 稳定性 | 稳定 | 稳定 | 不稳定 | 不稳定 | 稳定 | 稳定 |
| 时间复杂度 | O(n^2) | O(n^2) | O(n^2) | O(nlgn) | O(nlogn) | O(n^(3/2) ) |
| 空间复杂度 | O(1) | O(1) | O(1) | O(1) | O(n) | O(1) |
从时间复杂度(性能)上来说,一般选择快速排序,是一种排序比较快的排序方法
从稳定性来说,一般选择的是归并排序





)











——Python)

)