AC通道:http://www.lydsy.com/JudgeOnline/problem.php?id=2844
这题貌似HDU上有一道差不多的题,不过我没做过,也就没管了。
首先讲一个线性基的东西,大概就是这样:
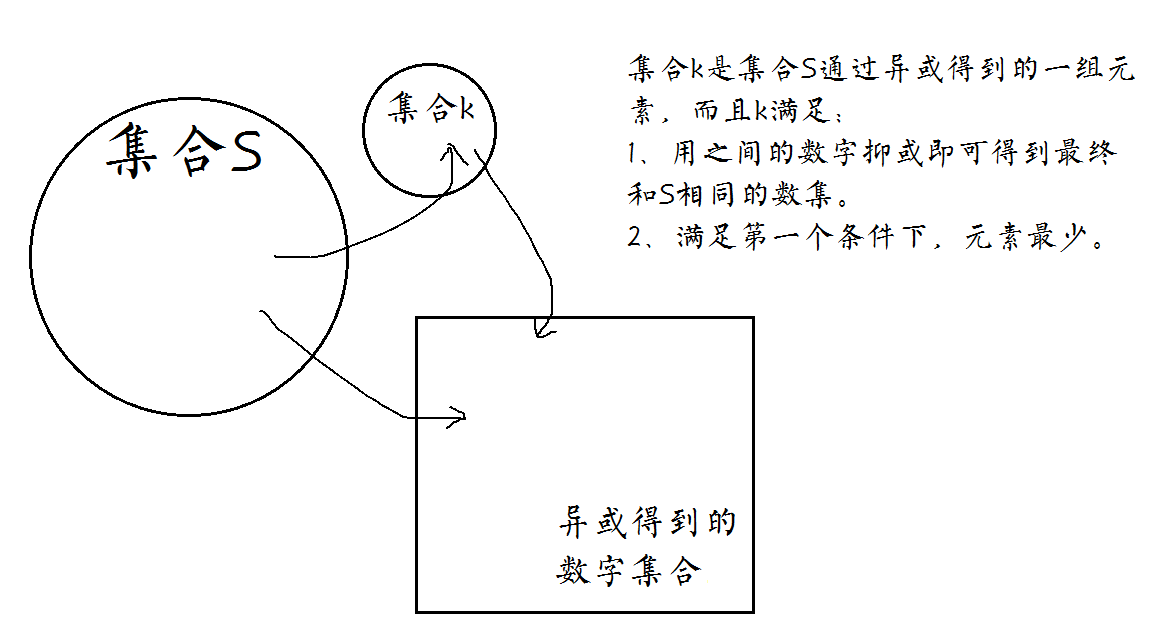
然后就是一个什么性质:S异或起来会出现重复,但是重复了多少次呢?
若我构造一个大小为k的线性基,那么重复了2^(n-k)次。
然后构造出需要的数,就每次找到能消去位数的地方消去就好。


#include<cstdio> #include<cstring> #include<algorithm>using namespace std;const int maxn=100010; const int mod=10086;inline int in(){int x=0;char ch=getchar();while(ch<'0' || ch>'9') ch=getchar();while(ch>='0' && ch<='9') x=10*x+ch-'0',ch=getchar();return x; }int n,m,k; int a[maxn],b[maxn];void gauss(){k=n;for(int i=1;i<=n;i++){for(int j=i+1;j<=n;j++)if(a[j]>a[i]) swap(a[i],a[j]);if(!a[i]){k=i-1;break;}for(int j=30;j>=0;j--)if((a[i]>>j)&1){b[i]=j;for(int x=1;x<=n;x++)if(x!=i && (a[x]>>j)&1)a[x]^=a[i];break;}} } inline int power(int x,int y){int t=1;for(;y;y>>=1,x=x*x%mod)if(y&1) t=t*x%mod;return t; }int main(){ #ifndef ONLINE_JUDGEfreopen("2844.in","r",stdin);freopen("2844.out","w",stdout); #endifn=in();for(int i=1;i<=n;i++) a[i]=in();m=in();gauss();int ans=1;for(int i=1;i<=k;i++)if((m>>b[i])&1){m^=a[i];ans=(ans+power(2,n-i))%mod;}printf("%d",ans); return 0; }




)











——Python)

)
