前言

突然就想分析一下全卷积网络的转置卷积部分了, 就是这么猝不及防的想法, 而且这个网络对图片的输入大小无要求，这么神奇的网络是时候分析一波了，我个人的学习方法调试代码，然后对照论文看理论

本次分析主要针对每层的权重大小和特征图大小的推导分析, 最最重要的是转置卷积部分是如何将特征图慢慢扩张到原始图片大小的.

国际惯例, 参考博客:

FCN的caffe实现戳这里

FCN学习:Semantic Segmentation

全卷积网络（FCN）与图像分割

如何理解深度学习中的deconvolution networks？

如何理解空洞卷积（dilated convolution）？

本文所需文件戳这里,一个模型, 一个网络结构,两张测试图片
链接: https://pan.baidu.com/s/1hseRZ5i 密码: e94k

运行代码

python

官方提供的代码是python文件, 我直接贴出来了, 因为我讨厌python调试代码

import numpy as np
from PIL import Image
import caffe
# load image, switch to BGR, subtract mean, and make dims C x H x W for Caffe
#im = Image.open('pascal/VOC2010/JPEGImages/2007_000129.jpg')
im = Image.open('2007_000175.jpg')
in_ = np.array(im, dtype=np.float32)
in_ = in_[:,:,::-1]
in_ -= np.array((104.00698793,116.66876762,122.67891434))
in_ = in_.transpose((2,0,1))
# load net
net = caffe.Net('voc-fcn8s/deploy.prototxt', 'voc-fcn8s/fcn8s-heavy-pascal.caffemodel', caffe.TEST)
# shape for input (data blob is N x C x H x W), set data
net.blobs['data'].reshape(1, *in_.shape)
net.blobs['data'].data[...] = in_
# run net and take argmax for prediction
net.forward()
out = net.blobs['score'].data[0].argmax(axis=0)

matlab

clear
clc
close all
addpath('../..')
caffe.reset_all
%读取图片
im=imread('2007_000129.jpg');
im=double(im);
im=im(:,:,[3 2 1]);%RGB->BGR
im(:,:,1)=im(:,:,1)-104.00698793;%B
im(:,:,2)=im(:,:,2)-116.66876762;%G
im(:,:,3)=im(:,:,3)-122.67891434;%R
im=permute(im,[2,1,3]);%(width,height,channel)->(C,H,W)
%读取模型
model_dir = './voc-fcn8s/';
net_model = [model_dir 'deploy.prototxt'];
net_weights = [model_dir 'fcn8s-heavy-pascal.caffemodel'];
net=caffe.Net(net_model,net_weights,'test')
%计算
net.blobs('data').reshape([size(im) 1]);
net.reshape();
out=net.forward({im});
[max_val,max_ind]=max(out{1},[],3);
%显示特征图
max_ind=max_ind-1;
max_ind=permute(max_ind,[2,1]);
max_ind=max_ind(end:-1:1,:);
contourf(max_ind)

直接贴个结果图,就是那个骑摩托车的jpg对应的分割图

【PS】关于matlab的代码是我自己瞎写的，如果有问题，欢迎在评论区指出

卷积特征图推导

直入主题，先看看网络结构(自己去NetScope把prototxt粘贴过去看,太大了), 然后我们一层一层推特征图大小, 看看转置卷积到底是何方神圣, 不过开始之前记住一个东东: 关于卷积的运算, 假设图像高度是M,卷积核高度是N, 对图像的填充(padding)是P, 卷积核移动步长为S, 则卷积后的特征图的高度是:

$$H'=\frac{M-N+2*P}{S}+1$$
对于特征图的宽度计算一样, 这个公式应该没问题吧

对于池化, 除不尽向上取整即可

对于转置卷积的高宽就是

$$M=(H'-1)*S-2*P+N$$
好了，开始计算，假设输入图像就是这个骑摩托的 2007_000129.jpg图像, 大小为 $(334,500,3)$, 此时你应该用 notepad++打开 deploy.prototxt了

先看看都有哪些层:

net.blob_names

输出

    'data''data_input_0_split_0''data_input_0_split_1''conv1_1''conv1_2''pool1''conv2_1''conv2_2''pool2''conv3_1''conv3_2''conv3_3''pool3''pool3_pool3_0_split_0''pool3_pool3_0_split_1''conv4_1''conv4_2''conv4_3''pool4''pool4_pool4_0_split_0''pool4_pool4_0_split_1''conv5_1''conv5_2''conv5_3''pool5''fc6''fc7''score_fr''upscore2''upscore2_upscore2_0_split_0''upscore2_upscore2_0_split_1''score_pool4''score_pool4c''fuse_pool4''upscore_pool4''upscore_pool4_upscore_pool4_0_split_0''upscore_pool4_upscore_pool4_0_split_1''score_pool3''score_pool3c''fuse_pool3''upscore8''score'

先看看输入数据大小:

size(net.blobs('data').get_data())ans =334   500     3

输入	输入大小(通道数,高,宽)	卷积核(个数,填充,高/宽,步长)/池化	输出(通道数,高,宽)	备注
data	(334,500,3)	-	-	输入
conv1_1	(334,500,3)	(64,100,3,1)	(64,532,698)	卷积
conv1_2	(64,532,698)	(64,1,3,1)	(64,532,698)	卷积
pool1	(64,532,698)	(2,2)	(64,266,349)	池化
conv2_1	(64,266,349)	(128,1,3,1)	(128,266,349)	卷积
conv2_2	(128,266,349)	(128,1,3,1)	(128,266,349)	卷积
pool2	(128,266,349)	(2,2)	(128,133,175)	池化
conv3_1	(128,133,175)	(256,1,3,1)	(256,133,175)	卷积
conv3_2	(256,133,175)	(256,1,3,1)	(256,133,175)	卷积
conv3_3	(256,133,175)	(256,1,3,1)	(256,133,175)	卷积
pool3	(256,133,175)	(2,2)	(256,67,88)	池化
conv4_1	(256,67,88)	(512,1,3,1)	(512,67,88)	卷积
conv4_2	(512,67,88)	(512,1,3,1)	(512,67,88)	卷积
conv4_3	(512,67,88)	(512,1,3,1)	(512,67,88)	卷积
pool4	(512,67,88)	(2,2)	(512,34,44)	池化
conv5_1	(512,34,44)	(512,1,3,1,)	(512,34,44)	卷积
conv5_2	(512,34,44)	(512,1,3,1)	(512,34,44)	卷积
conv5_3	(512,34,44)	(512,1,3,1)	(512,34,44)	卷积
pool5	(512,34,44)	(2,2)	(512,17,22)	池化
fc6	(512,17,22)	(4096,0,7,1)	(4096,11,16)	卷积
fc7	(4096,11,16)	(4096,0,1,1)	(4096,11,16)	卷积
score_fr	(4096,11,16)	(21,0,1,-)	(21,11,16)	卷积
upscore2	(21,11,16)	(21,-,4,2)	(21,24,34)	转置卷积
score_pool4	pool4	(21,0,1,-)	(21,34,44)	卷积
score_pool4c	upscore2,score_pool4	-	(21,24,34)	裁切
fuse_pool4	score_pool4c, upscore2	-	(21,24,34)	元素级加和
upscore_pool4	fuse_pool4	(21,-,4,2)	(21,50,70)	转置卷积
score_pool3	pool3	(21,0,1,-)	(21,67,88)	卷积
score_pool3c	fuse_pool4,pool3	-	(21,50,70)	裁剪
fuse_pool3	upscore_pool4, score_pool3c	-	(21,50,70)	元素级相加
upscore8	fuse_pool3	(21,-,16,8)	(21,408,568)	转置卷积
score	input, upscore8	-	(21,334,500)	裁剪

如果有兴趣的话, 可以使用我前面提供的可视化方法将特征图可视化看看, 贴一个部分可视化代码

function [  ] = feature_partvisual( net,mapnum,crop_num )
names=net.blob_names;
names{mapnum}
featuremap=net.blobs(names{mapnum}).get_data();%获取指定层的特征图
[m_size,n_size,num,~]=size(featuremap);%获取特征图大小，长*宽*卷积核个数*通道数
row=ceil(sqrt(num));%行数
col=row;%列数
feature_map=zeros(n_size*col,m_size*row);%因为opencv读取的图像高刚好是特征图的宽
cout_map=1;
for i=0:row-1for j=0:col-1if cout_map<=numfeature_map(j*n_size+1:(j+1)*n_size,i*m_size+1:(i+1)*m_size)=(mapminmax(featuremap(:,:,cout_map,crop_num),0,1)*255)';cout_map=cout_map+1;endend
end
imshow(uint8(feature_map))
str=strcat('feature map num:',num2str(cout_map-1));
title(str)
end

参数分别是:①net已经进行过一次前向计算的网络,这个网络现在已经充满了参数和特征图, ②mapnum是第几层的特征图, ③ crop_num是第几个图片的特征图需要被显示出来, 比如我丢进去十张图片, 只想显示第五张图片对应的特征图, 就把这个参数设置成5. 本例中, 如果想显示conv1_1的特征图可以这样调用feature_partvisual(net,4,1), 结果是

重要的层

接下来分析一下哪些层对网络结构挺重要的

转置卷积层

调用方法

layer {name: "upscore2"type: "Deconvolution"bottom: "score_fr"top: "upscore2"param {lr_mult: 0}convolution_param {num_output: 21bias_term: falsekernel_size: 4stride: 2}
}

直接贴一下相关的参考文献吧, 后面学习theano的转置卷积再详细看看这部分的理论推导

如何理解深度学习中的deconvolution networks？

What are deconvolutional layers?
A technical report on convolution arithmetic in the context of deep learning

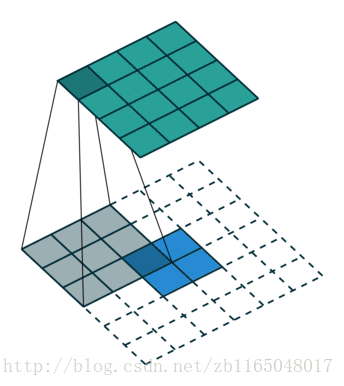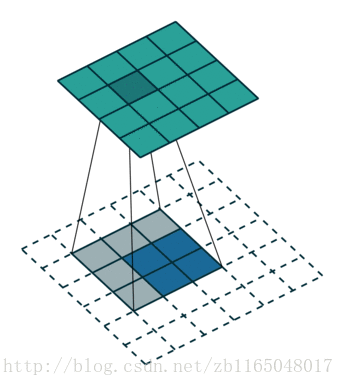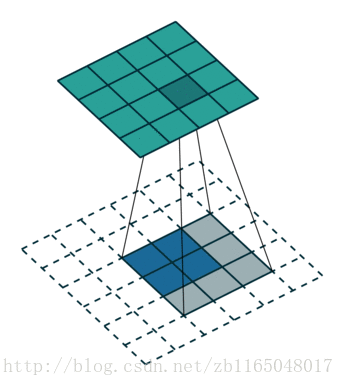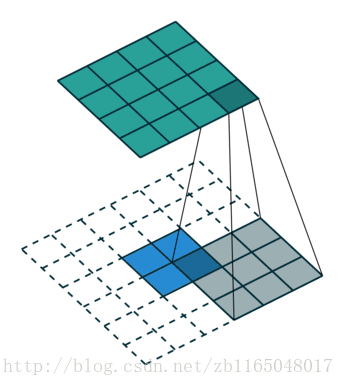
简单看看两个图, 第一个是对于步长为1,没有padding填充的卷积核的转置卷积过程,也就是(4*4)的图像经过(3*3)的卷积核得到(2*2)的操作的逆过程

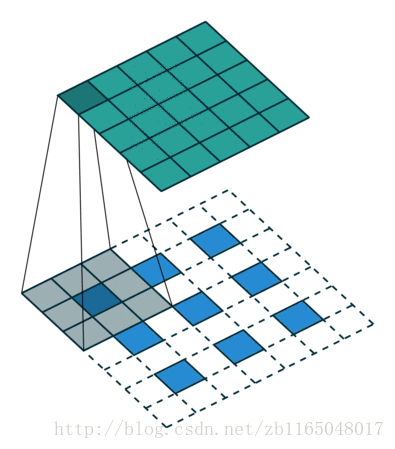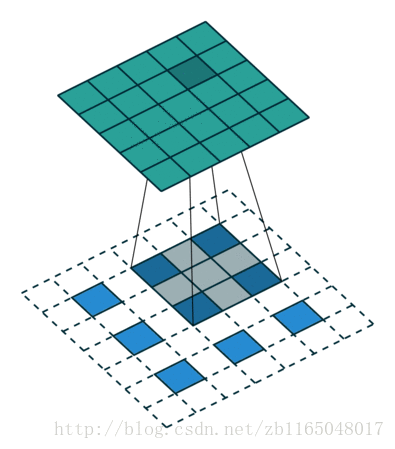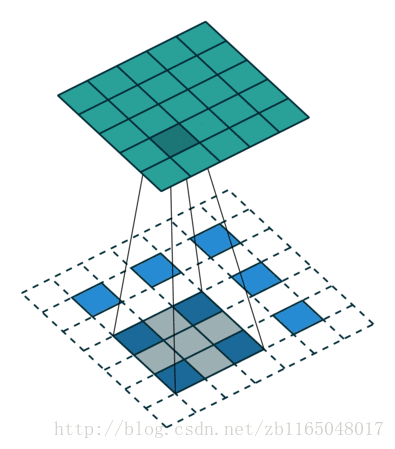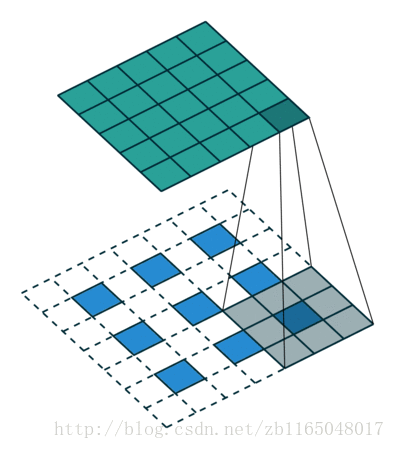
第二个是对于步长为2, padding填充为1的卷积核对应的转置卷积过程:也就是(5*5)的图像被padding填充1次以后, 经过(3*3)的卷积核步长为2以后得到(3*3)的操作的逆过程

裁剪

调用方法

layer {name: "score_pool4c"type: "Crop"bottom: "score_pool4"bottom: "upscore2"top: "score_pool4c"crop_param {axis: 2offset: 5}
}

作用可以戳这里看, 其实就是以第二个bottom的大小为参考,将第一个bottom裁剪成同样大小, axis=2表示从第二个轴开始裁剪(轴的编号是从1开始的), offset=5代表从当前轴的第五个元素开始取值,长度为第二个bottom的对应维度大小

元素级相加

将两个同样大小的矩阵的对应位置相加

调用方法为

layer {name: "fuse_pool4"type: "Eltwise"bottom: "upscore2"bottom: "score_pool4c"top: "fuse_pool4"eltwise_param {operation: SUM}
}

后记

这个网络的优势在于后面的全连接变成了使用卷积核, 这样对图片大小的输入就没有严格要求了, 因为全连接参数固定, 而卷积核只需要在同一张图片滑动即可,重构过程的网络设计还是很严格的, 一定要严格注意各种裁剪, 各种转置卷积的参数(包含padding和stride等).

这里网络设计几个技巧就是

• 一个特征图经过(个数,填充padding=1,卷积核大小=3,步长stride=1)的卷积核卷积以后, 特征图大小是不变的. 然后通过转置卷积就可以越卷越大了.
• 一个pool和另一个特征图拼接起来的方法就是按照最小的那个特征图大小对另一个进行裁剪, 然后再把这两个同样大小的特征图相加就行了

后续可能就要关注转置卷积的具体推导过程了, 如果有兴趣请继续关注博客后续

如果有错误地方，谢谢在评论区指正.