前言

前面学习了受限玻尔兹曼机(RBM)的理论和搭建方法, 如果稍微了解过的人, 肯定知道利用RBM可以堆叠构成深度信念网络(deep belief network, DBN)和深度玻尔兹曼机(deep Boltzmann machine), 这里就先学习一下DBN.

国际惯例, 参考博文:

Deep Belief Networks

A fast learning algorithm for deep belief nets

理论

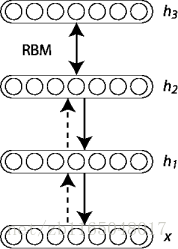
DBN的网络结构就是简单地将RBM堆叠起来, 样子长得就跟全连接一样.

由于它也是图模型, 所以很容易写出所有层的联合分布, 需要注意的是训练方法是逐层训练, 也就是说每两层是作为一个RBM训练的, 与其它层无关, 也即遇到类似于$P(h_2|x,h_1)$的可以直接写成$P(h_2|h_1)$, 表示$h_2$的训练与$x$无关, 了解到这, 我们就可以写联合分布了, 注意为了保持与教程一致, 此处采用的是以隐层为条件的可见层概率分布, 其实常规思维是以可见层为条件的隐层概率分布, 依据我前面介绍过的图模型联合概率分布计算方法:

$$\begin{aligned} P(x,h_1,h_2,\cdots,h_l)&=P(h_l)P(h_{l-1}|h_l)*P(h_{l-2}|h_{l-1},h_l)*\cdots P(x|h_l,h_{l-1},\cdots,h_1)\\ &=P(h_l)P(h_{l-1}|h_l)*P(h_{l-2}|h_{l-1})*\cdots*P(x|h_1)\\ &=P(h_l,h_{l-1})\Pi_{k=0}^{l-2}(P(h_k|h_{k+1})) \end{aligned}$$
上式中最后一步是将$h_0=x$, 进而整个DBN的训练方法就显而易见了:

• 将第一层作为一个RBM训练, 输入是$x=h^{(0)}$, 作为可见层
• 将第一层得到是输入表示作为第二层的数据输入, 有两种方案, 可以使用$P(h^{(1)}=1|h^{(0)})$的平均激活, 或者是从$P(h^{(1)}|h^{(0)})$采样, 个人觉得前者是针对二值输入, 后者是真对实值输入
• 将第二层作为RBM训练, 将变换数据(样本或均值激活)作为训练样本
• 重复第二步和第三步
• 最后就是微调整个网络参数,就是传说中的fine-tuning, 两种方法, 第一种是使用负对数似然损失的代理方法, 其实论文里面说的就是从上之下的一个算法, 也是Hinton大佬发明的wake-sleep算法, 这个算法经常被用于预训练AE(详细请看《视觉机器学习20讲》); 另一种方法就是有监督学习算法, 在模型顶上加个分类器作为误差传递的来源.

在教程中, 主要关注监督梯度下降的微调算法, 具体来说就是使用Logistic回归分类器基于DBN最后一层隐单元的输出对输入$x$分类. 随后通过负对数似然损失来执行有监督梯度下降, 由于有监督梯度对于权重和隐单元偏置非零(对每层RBM的可见层是零), 这就等价于通过无监督的方式, 为一个深层多层感知器(MLP)进行权重和隐单元偏置的初始化.

为什么这种训练方法有效？

拿具有两个隐层($h^{(1)},h^{(2)}$)的DBN来说, 权重分别为$W^{(1)},W^{(2)}$, Hinton在论文 中建立了一个式子$\log p(x)$, 如果不懂这个符号的含义, 建议去看看RBM的证明, 戳这里有一个非常非常好的RBM证明文档, 极为清晰, 极力推荐去看看.

$$\begin{aligned} \log p(x)=&KL(Q(h^{(1)}|x)\parallel p(h^{(1)}|x))\\ &+H_{Q(h^{(1)}|x)}\\ &+\sum_h Q(h^{(1)}|x)(\log p(h^{(1)})+\log p(x|h^{(1)})) \end{aligned}$$
细心点会发现教程提供的这个式子与 Hinton的论文中不同, 但是可以转化过去的, 你需要了解KL散度的知识, 我原来写过一篇博文, 戳 这里, 然后我们对上式进行变换, 得到 论文的表达形式
$$\begin{aligned} \log p(x)&= \begin{aligned} &KL(Q(h^{(1)}|x)\parallel p(h^{(1)}|x))\\ &+H_{Q(h^{(1)}|x)}\\ &+\sum_h Q(h^{(1)}|x)(\log p(h^{(1)})+\log p(x|h^{(1)})) \end{aligned}\\ &= \begin{aligned} &\sum_h H_{(Q(h^{(1)}|x),p(h^{(1)}|x))}-H_{(Q(h^{(1)}|x))}\\ &+H_{Q(h^{(1)}|x)}\\ &+\sum_h Q(h^{(1)}|x)\left[\log p(h^{(1)})+\log p(x|h^{(1)})\right] \end{aligned}\\ &=-\sum_h Q(h^{(1)}|x)\log p(h^{(1)}|x)+\sum_hQ(h^{(1)}|x)\left[\log p(h^{(1)})+\log p(x|h^{(1)})\right] \end{aligned}$$
边界情况就是 $KL(Q(h^{(1)}|x)|p(h^{(1)}|x))=0$, 即由模型根据输入向量得到的特征向量与原始数据本来的真正的特征向量相等, 那么 $Q(h^{(1)}|x)=p(h^{(1)}|x)$, 最终上式结果可以写成
$$\log p(x)=-\sum_h Q(h^{(1)}|x)\log Q(h^{(1)}|x)+\sum_hQ(h^{(1)}|x)\left[\log p(h^{(1)})+\log p(x|h^{(1)})\right]$$
可以发现这个式子与论文的式子完全相同.

正如论文说的, $h^{(0)}$是第一个隐层的二值向量, $p(h^{(0)})$是当前模型$h^{(0)}$的先验概率, $Q(\cdot |x)$是基于第一层隐层为条件的任意概率分布, 边界就是当且仅当$Q(\cdot|x)$是真实的后验分布. 当所有的权重被绑定在一起的时候, 将$W_1^{T}$应用到数据向量计算得到基于$h^{(1)}$的因子分布是真实的后验分布. 因而在贪婪算法的第二步$\log p(x)$是等于边界的. 第二步将$Q(\cdot|x)$和$p(x|h^{(1)})$固定, 边界的导数与下式的导数一样

$$\sum Q(h^{(1)}|x)\log p(h^{(1)})$$
因而最大化高层的比如说权重的边界实际上等价于最大化数据集的对数概率, 其中 $h^{(1)}$是由 $Q(h^{(1)}|x)$产生的. 如果边界变得更加紧密, $\log p(x)$有极大可能降低, 即使基于它的较低的边界增加, 但是 $\log p(x)$不会低于第二步贪婪算法得到的它的值, 因为边界是很紧密的而且经常处于上升趋势

代码实现

可以发现DBN与SdA非常相似, 因为他们都是无监督的层级训练, 主要区别就是DBN使用层级训练基础是RBM, 而SdA使用的层级训练基础是dA. 最好复习一下dA的梯度是由什么损失函数得到的, 这样有助于与RBM做一个区分.

因为采用DBN做无监督训练, 然后采用MLP微调, 所以直接先建立一个DBN类去作为MLP的层. 因而还是需要用到我们之前的代码, 包含:

• 引入各种包

  import numpy as np
  import theano
  import theano.tensor as T
  from theano.tensor.shared_randomstreams import RandomStreams
  import cPickle,gzip
  from PIL import Image
  import pylab
  import os

• 读取数据的函数

  
  #定义读数据的函数,把数据丢入到共享区域def load_data(dataset):data_dir,data_file=os.path.split(dataset)if os.path.isfile(dataset):with gzip.open(dataset,'rb') as f:train_set,valid_set,test_set=cPickle.load(f)#共享数据集def shared_dataset(data_xy,borrow=True):data_x,data_y=data_xyshared_x=theano.shared(np.asarray(data_x,dtype=theano.config.floatX),borrow=borrow)shared_y=theano.shared(np.asarray(data_y,dtype=theano.config.floatX),borrow=borrow)return shared_x,T.cast(shared_y,'int32')#定义三个元组分别存储训练集,验证集,测试集train_set_x,train_set_y=shared_dataset(train_set)valid_set_x,valid_set_y=shared_dataset(valid_set)test_set_x,test_set_y=shared_dataset(test_set)rval=[(train_set_x,train_set_y),(valid_set_x,valid_set_y),(test_set_x,test_set_y)]return rval

• 定义RBM作为预训练的基础, 主要有positive phase、negative phase, 构成Gibbs sampling, 还有能量函数的定义以及使用能量函数做梯度更新的方法

  
  #定义RBMclass RBM(object):def __init__(self,rng=None,trng=None,input=None,n_visible=784,n_hidden=500,W=None,hbias=None,vbias=None):self.n_visible=n_visibleself.n_hidden=n_hiddenif rng is None:rng=np.random.RandomState(1234)if trng is None:trng=RandomStreams(rng.randint(2**30))#初始化权重和偏置    if W is None:initW=np.asarray(rng.uniform(low=-4*np.sqrt(6./(n_hidden+n_visible)),high=4*np.sqrt(6./(n_hidden+n_visible)),size=(n_visible,n_hidden)),dtype=theano.config.floatX)W=theano.shared(value=initW,name='W',borrow=True)if hbias is None:inithbias=np.zeros(n_hidden,dtype=theano.config.floatX)hbias=theano.shared(value=inithbias,name='hbias',borrow=True)if vbias is None:initvbias=np.zeros(n_visible,dtype=theano.config.floatX)vbias=theano.shared(value=initvbias,name='vbias',borrow=True)self.input=inputif not input:self.input=T.matrix('input')self.W=Wself.hbias=hbiasself.vbias=vbiasself.trng=trngself.params=[self.W,self.hbias,self.vbias]##########前向计算,从可见层到隐层#################激活概率def propup(self,vis):pre_sigmoid_activation=T.dot(vis,self.W)+self.hbiasreturn [pre_sigmoid_activation,T.nnet.sigmoid(pre_sigmoid_activation)]#二值激活def sample_h_given_v(self,v0_samples):pre_sigmoid_h1,h1_mean=self.propup(v0_samples)h1_sample=self.trng.binomial(size=h1_mean.shape,n=1,p=h1_mean,dtype=theano.config.floatX)return [pre_sigmoid_h1,h1_mean,h1_sample]##########反向计算,从隐层到可见层#################激活概率def propdown(self,hid):pre_sigmoid_activation=T.dot(hid,self.W.T)+self.vbiasreturn [pre_sigmoid_activation,T.nnet.sigmoid(pre_sigmoid_activation)]#二值激活def sample_v_given_h(self,h0_samples):pre_sigmoid_v1,v1_mean=self.propdown(h0_samples)v1_sample=self.trng.binomial(size=v1_mean.shape,n=1,p=v1_mean,dtype=theano.config.floatX)return [pre_sigmoid_v1,v1_mean,v1_sample]##########吉布斯采样#################可见层->隐层->可见层def gibbs_vhv(self,v0_samples):pre_sigmoid_h1,h1_mean,h1_sample=self.sample_h_given_v(v0_samples)pre_sigmoid_v1,v1_mean,v1_sample=self.sample_v_given_h(h1_sample)return [pre_sigmoid_v1,v1_mean,v1_sample,pre_sigmoid_h1,h1_mean,h1_sample]############自由能量函数###############def free_energy(self,v_samples):wx_b=T.dot(v_samples,self.W)+self.hbiasvbias_term=T.dot(v_samples,self.vbias)#第一项hidden_term=T.sum(T.log(1+T.exp(wx_b)),axis=1)#第二项return -hidden_term-vbias_term############梯度更新#################def get_cost_updates(self,lr=0.1,k=1):([pre_sigmoid_nvs,nv_means,nv_samples,pre_sigmoid_nhs,nh_means,nh_samples],updates)=\theano.scan(self.gibbs_vhv,outputs_info=[None,None,self.input,None,None,None],n_steps=k,name='gibbs_vhv')chain_end=nv_samples[-1]cost=T.mean(self.free_energy(self.input))-T.mean(self.free_energy(chain_end))gparams=T.grad(cost,self.params,consider_constant=[chain_end])for gparam,param in zip(gparams,self.params):updates[param]=param-gparam*T.cast(lr,dtype=theano.config.floatX)##################期望看到交叉熵损失##############monitor_cost=self.get_reconstruction_cost(pre_sigmoid_nvs[-1])return monitor_cost,updates########非持续性对比散度,重构误差#########def get_reconstruction_cost(self,pre_sigmoid_nv):cross_entropy=T.mean(T.sum(self.input*T.log(T.nnet.sigmoid(pre_sigmoid_nv))+\(1-self.input)*T.log(1-T.nnet.sigmoid(pre_sigmoid_nv)),axis=1))return cross_entropy

• 搭建MLP需要的隐层定义

  
  #定义多层感知器的隐层单元相关操作class HiddenLayer(object):def __init__(self,rng,input,n_in,n_out,W=None,b=None,activation=T.tanh):self.input=inputif W is None:W_values=np.asarray(rng.uniform(low=- np.sqrt(6./(n_in+n_out)),high= np.sqrt(6./(n_in+n_out)),size=(n_in,n_out)),dtype=theano.config.floatX)if activation==T.nnet.sigmoid:W_values *= 4W=theano.shared(value=W_values,name='W',borrow=True)if b is None:b_vaules=np.zeros((n_out,),dtype=theano.config.floatX)b=theano.shared(value=b_vaules,name='b',borrow=True)self.W=Wself.b=blin_output=T.dot(input,self.W)+self.b#未被激活的线性操作self.output=(lin_output if activation is None else activation(lin_output))self.params=[self.W,self.b]

• 最后微调需要softmax

  
  #定义最后一层softmaxclass LogisticRegression(object):def __init__(self,input,n_in,n_out):#共享权重self.W=theano.shared(value=np.zeros((n_in,n_out),dtype=theano.config.floatX),name='W',borrow=True)#共享偏置self.b=theano.shared(value=np.zeros((n_out,),dtype=theano.config.floatX),name='b',borrow=True)#softmax函数self.p_y_given_x=T.nnet.softmax(T.dot(input,self.W)+self.b)#预测值self.y_pred=T.argmax(self.p_y_given_x,axis=1)self.params=[self.W,self.b]#模型参数self.input=input#模型输入#定义负对数似然def negative_log_likelihood(self,y):return -T.mean(T.log(self.p_y_given_x)[T.arange(y.shape[0]),y])#定义误差def errors(self, y):# check if y has same dimension of y_predif y.ndim != self.y_pred.ndim:raise TypeError('y should have the same shape as self.y_pred',('y', y.type, 'y_pred', self.y_pred.type))# check if y is of the correct datatypeif y.dtype.startswith('int'):# the T.neq operator returns a vector of 0s and 1s, where 1# represents a mistake in predictionreturn T.mean(T.neq(self.y_pred, y))else:raise NotImplementedError()

准备工作完成以后, 可以进行DBN的定义了, 首先定义结构, 主要包含多个隐层, RBM的逐层训练, 由于MLP和多个RBM是共享隐单元的, 所以无需重复定义, 但是最后需要使用softmax层作为微调梯度的来源.

class DBN(object):def __init__(self,rng=None,trng=None,n_visible=784,n_hidden=[500,500],n_out=10):self.sigmoid_layers=[]self.rbm_layers=[]self.params=[]self.n_layers=len(n_hidden)assert self.n_layers>0if not trng:trng=RandomStreams(rng.randint(2**30))self.x=T.matrix('x')#输入self.y=T.ivector('y')#标签for i in range(self.n_layers):#初始化各隐层if i==0:input_size=n_visibleelse:input_size=n_hidden[i-1]if i==0:layer_input=self.xelse:layer_input=self.sigmoid_layers[-1].output#建立隐层sigmoid_layer=HiddenLayer(rng=rng,input=layer_input,n_in=input_size,n_out=n_hidden[i],activation=T.nnet.sigmoid)self.sigmoid_layers.append(sigmoid_layer)self.params.extend(sigmoid_layer.params)#逐层预训练rbm_layer=RBM(rng=rng,trng=trng,input=layer_input,n_visible=input_size,n_hidden=n_hidden[i],W=sigmoid_layer.W,hbias=sigmoid_layer.b)self.rbm_layers.append(rbm_layer)#微调分类层self.logLayer=LogisticRegression(input=self.sigmoid_layers[-1].output,n_in=n_hidden[-1],n_out=n_out)self.params.extend(self.logLayer.params)self.finetune_cost=self.logLayer.negative_log_likelihood(self.y)self.errors=self.logLayer.errors(self.y)

这里一定要注意微调分类层不是包含在for循环中的, 虽然大家都知道, 但是写代码就是容易发生这个对齐情况, 我当时就写错了, 找了半天错误, 错误提示是

构建DBN
预训练开始
第0层第0次迭代, 损失-98
第1层第0次迭代, 损失-332
第2层第0次迭代, 损失-52
开始微调
---------------------------------------------------------------------------
DisconnectedInputError                    Traceback (most recent call last)
<ipython-input-13-1ad031bf1afb> in <module>()
----> 1 test_DBN()<ipython-input-12-1ea97c3e407d> in test_DBN(pretrain_lr, k, pretrain_epoches, finetune_lr, train_epoch, dataset, batch_size)18             print('第%d层第%d次迭代, 损失%d' %(i,epoch,np.mean(c,dtype='float64')))19     print('开始微调')
---> 20     train_fn,validate_model,test_model=dbn.finetune(datasets=datasets,batch_size=batch_size,learning_rate=finetune_lr)21     patience=4*n_train_batches22     patience_inc=2.0<ipython-input-11-f24396c0dd18> in finetune(self, datasets, batch_size, learning_rate)78 79         index=T.lscalar('index')
---> 80         gparams=T.grad(self.finetune_cost,self.params)81         updates=[]82         for param,gparam in zip(self.params,gparams):C:\ProgramData\Anaconda2\lib\site-packages\theano\gradient.pyc in grad(cost, wrt, consider_constant, disconnected_inputs, add_names, known_grads, return_disconnected, null_gradients)537         if elem not in var_to_app_to_idx and elem is not cost \538                 and elem not in grad_dict:
--> 539             handle_disconnected(elem)540             grad_dict[elem] = disconnected_type()541 C:\ProgramData\Anaconda2\lib\site-packages\theano\gradient.pyc in handle_disconnected(var)524             elif disconnected_inputs == 'raise':525                 message = utils.get_variable_trace_string(var)
--> 526                 raise DisconnectedInputError(message)527             else:528                 raise ValueError("Invalid value for keyword "DisconnectedInputError:  
Backtrace when that variable is created:File "C:\ProgramData\Anaconda2\lib\site-packages\ipykernel\zmqshell.py", line 533, in run_cellreturn super(ZMQInteractiveShell, self).run_cell(*args, **kwargs)File "C:\ProgramData\Anaconda2\lib\site-packages\IPython\core\interactiveshell.py", line 2718, in run_cellinteractivity=interactivity, compiler=compiler, result=result)File "C:\ProgramData\Anaconda2\lib\site-packages\IPython\core\interactiveshell.py", line 2828, in run_ast_nodesif self.run_code(code, result):File "C:\ProgramData\Anaconda2\lib\site-packages\IPython\core\interactiveshell.py", line 2882, in run_codeexec(code_obj, self.user_global_ns, self.user_ns)File "<ipython-input-13-1ad031bf1afb>", line 1, in <module>test_DBN()File "<ipython-input-12-1ea97c3e407d>", line 10, in test_DBNdbn=DBN(rng=rng,trng=RandomStreams(rng.randint(2**30)),n_visible=28*28,n_hidden=[1000, 500, 400],n_out=10)File "<ipython-input-11-f24396c0dd18>", line 49, in __init__n_out=n_out)File "<ipython-input-5-22c6bb9a49a7>", line 7, in __init__borrow=True)

然后就可以定义预训练过程了,逐层更新, 依旧是使用for循环

def pretrain(self,train_set,batch_size,k):index=T.lscalar('index')learning_rate=T.scalar('lr')batch_begin=index*batch_sizebatch_end=batch_begin+batch_sizepretrain_fns=[]for rbm in self.rbm_layers:cost,updates=rbm.get_cost_updates(learning_rate,k=k)fn=theano.function(inputs=[index,theano.In(learning_rate,value=0.1)],outputs=cost,updates=updates,givens={self.x:train_set[batch_begin:batch_end]})pretrain_fns.append(fn)return pretrain_fns

微调阶段与MLP的构建一样, 利用训练集更新参数, 利用验证集和测试集查看模型效果

def finetune(self,datasets,batch_size,learning_rate):(train_set_x,train_set_y)=datasets[0](valid_set_x,valid_set_y)=datasets[1](test_set_x,test_set_y)=datasets[2]n_valid_batches=valid_set_x.get_value(borrow=True).shape[0]n_valid_batches//=batch_sizen_test_batches=test_set_x.get_value(borrow=True).shape[0]n_test_batches//=batch_sizeindex=T.lscalar('index')gparams=T.grad(self.finetune_cost,self.params)updates=[]for param,gparam in zip(self.params,gparams):updates.append((param,param-gparam*learning_rate))train_fn=theano.function(inputs=[index],outputs=self.finetune_cost,updates=updates,givens={self.x:train_set_x[index*batch_size:(index+1)*batch_size],self.y:train_set_y[index*batch_size:(index+1)*batch_size]})valid_score=theano.function(inputs=[index],outputs=self.errors,givens={self.x:valid_set_x[index*batch_size:(index+1)*batch_size],self.y:valid_set_y[index*batch_size:(index+1)*batch_size]})test_score=theano.function(inputs=[index],outputs=self.errors,givens={self.x:test_set_x[index*batch_size:(index+1)*batch_size],self.y:test_set_y[index*batch_size:(index+1)*batch_size]})

对于验证集和测试集, 我们希望得到准确率信息

def valid():return [valid_score(i) for i in range(n_valid_batches)]def test():return [test_score(i) for i in range(n_test_batches)]return train_fn,valid,test

最终运行阶段, 首先初始化一个DBN网络

    datasets=load_data(dataset)train_set_x,train_set_y=datasets[0]n_train_batches=train_set_x.get_value(borrow=True).shape[0]//batch_sizeprint('构建DBN')rng=np.random.RandomState(123)trng=RandomStreams(rng.randint(2**30))dbn=DBN(rng=rng,trng=RandomStreams(rng.randint(2**30)),n_visible=28*28,n_hidden=[500, 200, 100],n_out=10)

然后正式逐层RBM预训练

    print('预训练开始')pretrain_fns=dbn.pretrain(train_set=train_set_x,batch_size=batch_size,k=k)for i in range(dbn.n_layers):for epoch in range(pretrain_epoches):c=[]for batch_index in range(n_train_batches):c.append(pretrain_fns[i](index=batch_index,lr=pretrain_lr))print('第%d层第%d次迭代, 损失%d' %(i,epoch,np.mean(c,dtype='float64')))

提前终止算法微调

 print('开始微调')train_fn,validate_model,test_model=dbn.finetune(datasets=datasets,batch_size=batch_size,learning_rate=finetune_lr)patience=4*n_train_batchespatience_inc=2.0imp_threshold=0.995valid_frequence=min(n_train_batches,patience/2)best_loss=np.inftest_socre=0.0done_loop=Falseepoch=0while(epoch<train_epoch) and (not done_loop):epoch=epoch+1for minibatch_index in range(n_train_batches):train_fn(minibatch_index)iter=(epoch-1)*n_train_batches+minibatch_indexif (iter+1)%valid_frequence==0:valid_loss=validate_model()this_valid_loss=np.mean(valid_loss,dtype='float64')print('第%d次迭代, 第%d个批次,验证误差为%f %%' %(epoch,minibatch_index+1,this_valid_loss*100))if this_valid_loss<best_loss:if this_valid_loss<best_loss*imp_threshold:patience=max(patience,iter*patience_inc)best_loss=this_valid_lossbest_iter=itertest_loss=test_model()test_score=np.mean(test_loss,dtype='float64')print('第%d次训练, 第%d批数据,测试误差为%f %%' %(epoch,minibatch_index+1,test_score*100.0))if patience<=iter:done_loop=Truebreak

模型的保存方法就不写了, 和MLP的差不多, 主要还是因为我python不是特别好, 搞不好又出一堆错误, 训练结果如下:

构建DBN
预训练开始
第0层第0次迭代, 损失-106
第1层第0次迭代, 损失-180
第2层第0次迭代, 损失-38
开始微调
第1次迭代, 第5000个批次,验证误差为5.360000 %
第1次训练, 第5000批数据,测试误差为6.100000 %
第2次迭代, 第5000个批次,验证误差为4.100000 %
第2次训练, 第5000批数据,测试误差为4.510000 %
第3次迭代, 第5000个批次,验证误差为3.490000 %
第3次训练, 第5000批数据,测试误差为4.030000 %
第4次迭代, 第5000个批次,验证误差为3.250000 %
第4次训练, 第5000批数据,测试误差为3.560000 %
第5次迭代, 第5000个批次,验证误差为3.020000 %
第5次训练, 第5000批数据,测试误差为3.320000 %
第6次迭代, 第5000个批次,验证误差为2.830000 %
第6次训练, 第5000批数据,测试误差为3.220000 %
第7次迭代, 第5000个批次,验证误差为2.790000 %
第7次训练, 第5000批数据,测试误差为2.990000 %
第8次迭代, 第5000个批次,验证误差为2.650000 %
第8次训练, 第5000批数据,测试误差为2.800000 %
第9次迭代, 第5000个批次,验证误差为2.600000 %
第9次训练, 第5000批数据,测试误差为2.690000 %
第10次迭代, 第5000个批次,验证误差为2.620000 %
第11次迭代, 第5000个批次,验证误差为2.570000 %
第11次训练, 第5000批数据,测试误差为2.580000 %
第12次迭代, 第5000个批次,验证误差为2.480000 %
第12次训练, 第5000批数据,测试误差为2.580000 %
第13次迭代, 第5000个批次,验证误差为2.460000 %
第13次训练, 第5000批数据,测试误差为2.590000 %
第14次迭代, 第5000个批次,验证误差为2.440000 %
第14次训练, 第5000批数据,测试误差为2.520000 %
第15次迭代, 第5000个批次,验证误差为2.370000 %
第15次训练, 第5000批数据,测试误差为2.500000 %
第16次迭代, 第5000个批次,验证误差为2.320000 %
第16次训练, 第5000批数据,测试误差为2.460000 %
第17次迭代, 第5000个批次,验证误差为2.310000 %
第17次训练, 第5000批数据,测试误差为2.510000 %
第18次迭代, 第5000个批次,验证误差为2.310000 %
第19次迭代, 第5000个批次,验证误差为2.260000 %
第19次训练, 第5000批数据,测试误差为2.430000 %
第20次迭代, 第5000个批次,验证误差为2.230000 %
第20次训练, 第5000批数据,测试误差为2.360000 %

后记

自己写代码的时候主要就是刚才提到的那个对齐错误, 导致整个程序的错误日志有点看不懂, 大概意思就是梯度更新的位置出现了问题, 但是导致梯度出问题的原因可能有很多, 当代码量较大的时候就不太好查找了, 所以大家写代码一定要仔细仔细仔细.

博文代码:链接: https://pan.baidu.com/s/1gfaTR6z 密码: fhe2