关于文章 Microfacet Models for Refraction through Rough Sufaces的一点笔记,欢迎指正。
BSDF
BSDF(Bidirectional Sacttering Distribution Function) 描述了光如何在物体表面散射。如果仅仅限制反射或者透射,BSDF经常被称作BRDF或者BTDF,然而BSDF将是BRDF,fs,BTDF,ft 项的综合作用。
微表面法线分布函数 D(m)
给定一个以m为中心的无穷小的立体角dwm和一个宏观表面积dA,D(m)dwm就是在wm 方向上微观表面投影在宏观表面上的面积比例。D是密度函数,单位是1/steradians,有着一下性质:
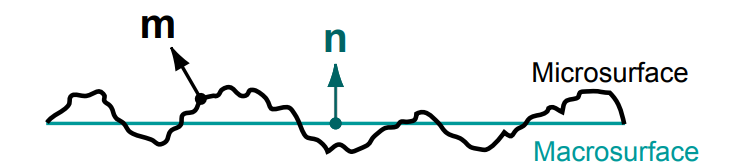
可以结合此图理解
1.
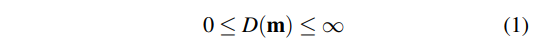
2.总的微表面面积至少和宏观面积一样大
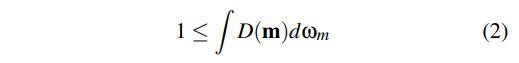
这里个人的理解是,D本身就是投影过的函数 (隐藏着一个cos 项,即从微观表面投影到宏观表面的投影项),所以在wm 的方向上的投影的面积至少和原先定义宏观面积dA一样大
3.在任何方向v上的微表面的投影是和宏观表面上的投影是一样的
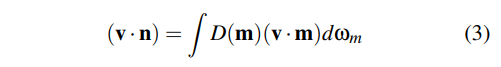
4.当v=n的时候
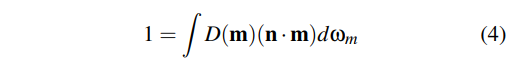
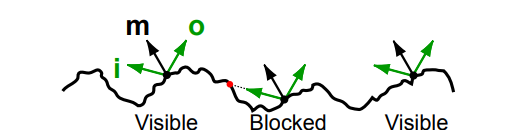
Shadowing-Masking函数 G
G(i,o,m) 描述了在法线方向m,从入射方向i,和出射方向o之间的可见度, 是对微表面的细节描写,
G(i,o,m)有着一下特性:
5.约束在[0,1]之间
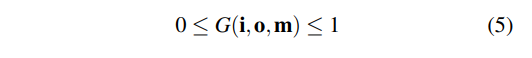
6. i, o方向都可见的话,则G是对称的
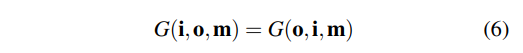
7.如果入射方向 i 或者出射方向 o 是在微表面的背面,则G = 0

整合BSDF
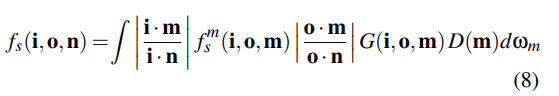
我们需要应用一个修正因子在入射微表面的irradiance和离开微表面的散射的radiance根据投影的面积测量。
接下来着重解释 fsm(i,o,m) 的含义
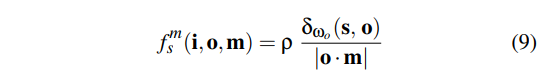
p代表从入射方向进入的能量
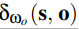
是Dirac delta函数, 在数学定义上是广义的函数。他们总是有着一个自己的度量值,例如在o方向的立体角dwo ,并且值由他们的积分来决定。
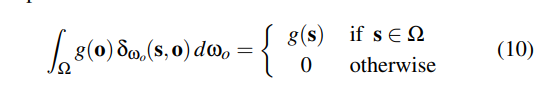
这里的g(o) 是任何函数。
在方程8中我们想要表达微表面法线和相关立体角之间的关系。假定对于任何的入射和出射方向,最多有一个微表面能够把能量从 i 散射到 o .为了计算方便,我们引入半程向量的概念,即 i 和 o 的法线方向 h(i,o), 用 h 和 微表面法线 m 来代替 i, o 。但由于Dirac增量函数是根据一个积分定义的,所以相当于积分换元。由此方程9可以写成:
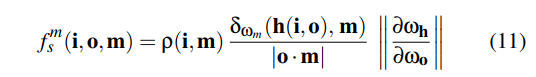
我们再此定义Jacobian
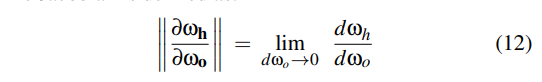
由于 fs m(i,o,m) = fr m(i,o,m) + ft m(i,o,m);
对于frm(i,o,m) 理想反射,我们有如下定义:
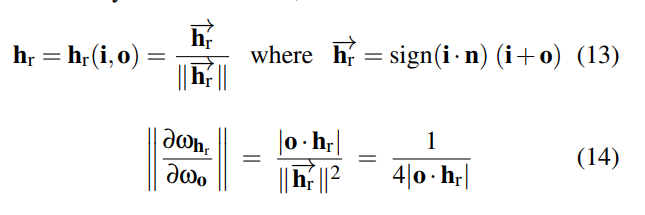
对于理想反射使用Fresnel factor F代表能量有多少被传递
把14式带入11式可得:
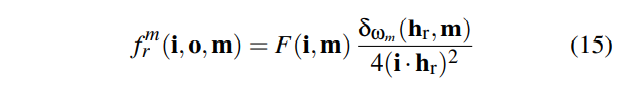
对于理想折射 ftm 来说 由于折射发生在表面两边 由此定义折射率ni no, 由于在两种不同的介质中,入射方向和出射方向会发生改变。Snell 定律可由半程向量ht 表达 由此可知:
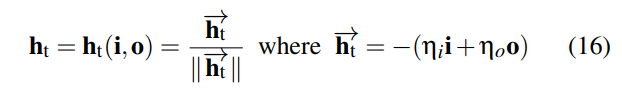
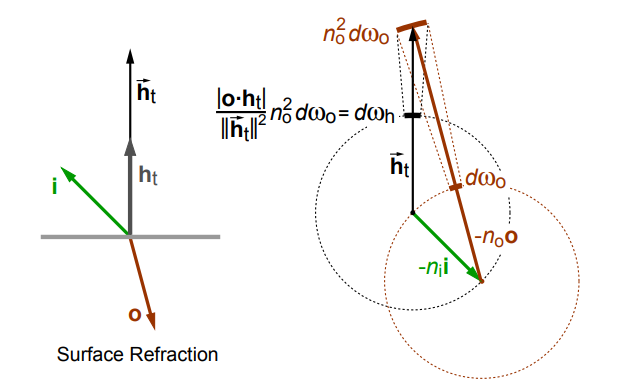
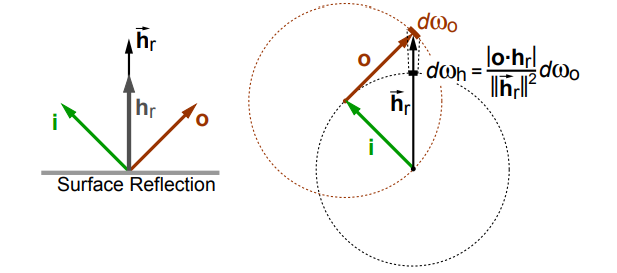
对于Jacobian来说 由上图可知
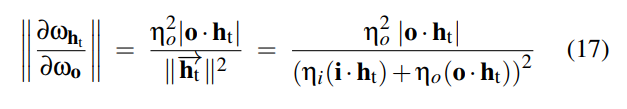
将17式带入11式中: 由于总能量被折射和反射,那么对于折射的能量将是 1 - F(i,m):
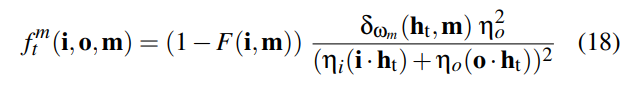
将frm 和ft m带替 fsm即可得最终式。
对于F D G的选择
对于F(i,m) 的选择,这里给出相应公式
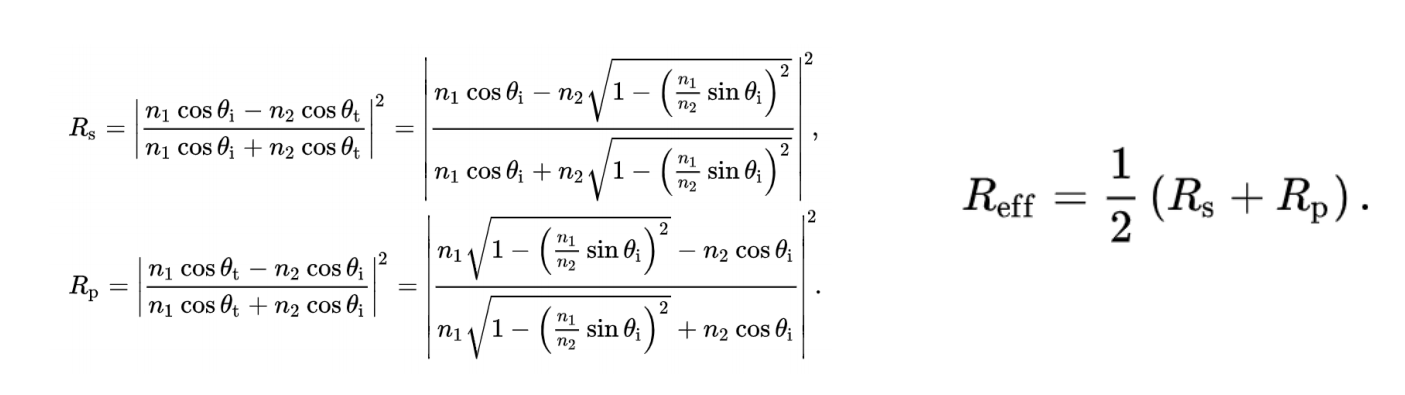
是不是感觉异常的复杂,这里再给出一种近似:Schlick近似
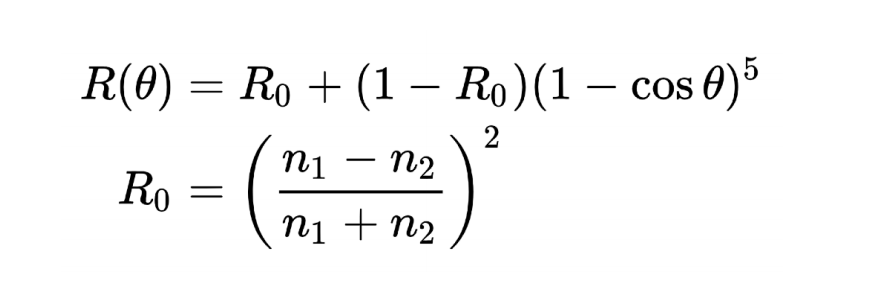
这个就相当简单了
对于G(i,o,m) 我们使用Smith近似,Smith近似假设入射和出射的可见度不相互影响即可以近似为
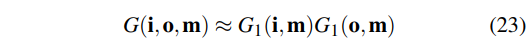
即从入射方向看向着色点和出射发向看向出射点的可见性。
对于法线分布,我们使用如下法线采样函数:
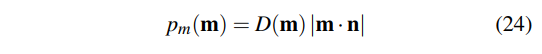
由于对于不同 的NDF(normal distribution function)来说 对应的采样函数和G(i,o,m)是不同的
所以这里仅介绍 (以下都是法线分布函数)
Beckmann Distribution
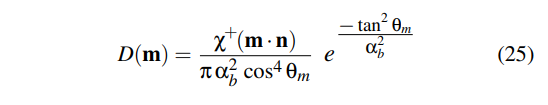
a即粗糙程度
相对应的G项
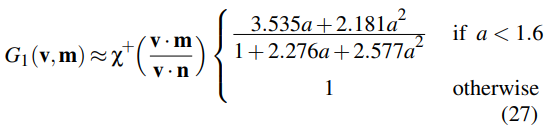
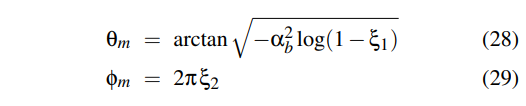
Phong Distribution
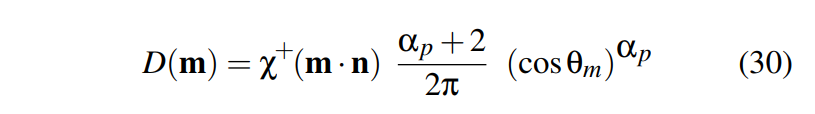
这里定义:
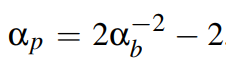
对于Smith G1 对于Phong模型没有解析的解,但由于Phong模型和Beckmann分布是非常相似的,Smith是依赖于NDF的,所以使用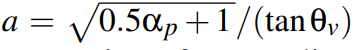
来带入27式,以便估计G项。
采样函数:
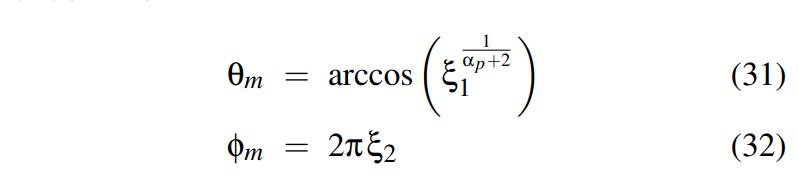
GGX Distribution(又名Trowbridge-Reitz 简称TR)

GGX又有tail函数之称,原因请看稍后的图像。
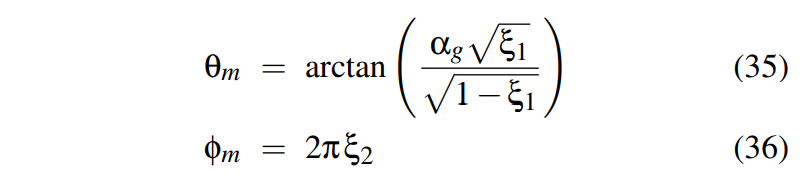
对于三种分布函数的图像化:

红线但又泛着蓝色的是Backmann和Phong的分布,绿线代表GGX函数从图中可以看见对于GGX而言在20多度的时候,下降缓慢,但不为0,这就是长尾巴的含义,同时也有着良好的性质。
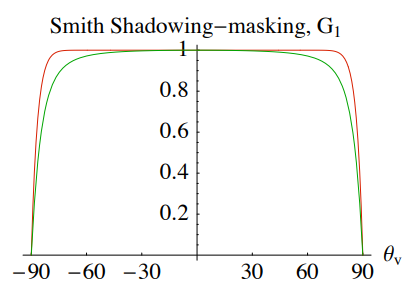
同理红线代表Backmann和Phong,绿线代表GGX, 入射方向基本和法线方向相同时,G项为1,不产生作用。
)



)





)

)

)

)


)