一副图像通过滤波器得到另一张图像,其中滤波器又称为卷积核,滤波的过程称之为卷积。

这就是一个卷积的过程,通过一个卷积核得到另一张图片,明显发现新的到的图片边缘部分更加清晰了(锐化)。
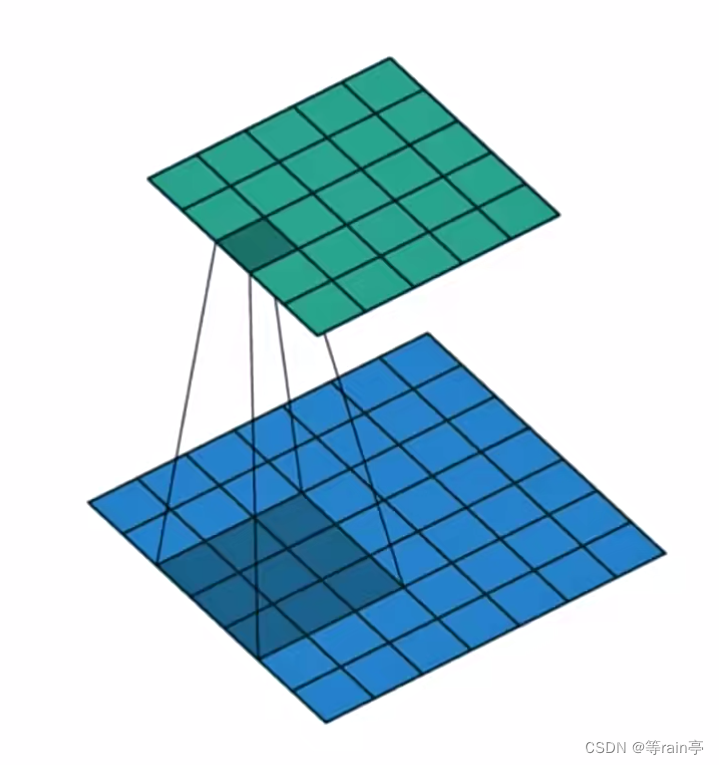
上图就是一个卷积的过程,下面的是原始图像,上面的是卷积核。卷积核以一定步长对于原始图像进行卷积处理,得到新的图像。
卷积核的大小:上图中的卷积核是5x5大小的卷积核。
锚点:就是卷积核最中心的位置
边界扩充:进行卷积后的图像一般比原始图像要小一点,为了和原始图像大小相同,就需要进行边界扩充。
步长:就是卷积核对原始图像进行扫描时,每一次移动几个像素。
卷积核的大小
(1)卷积核一般为奇数,如3x3,5x5,7x7;
一方面是为了增加padding的原因,就是进行扩充操作。
另一方面是保证锚点在中间(大家可以自己画一下3x3和4x4的矩阵进行思考有什么区别)防止位置发生偏移。
(2)卷积核大小的影响:卷积核越大,看到的信息(感受野)就越多,提取的特征就越好,同时计算量就越大。(目前很多深度学习领域中,使用两个或多个小的卷积核代替大的卷积核)
(3)边界扩充:当卷积核大于1且不进行边界扩充时,输出的尺寸一定会变小,所以需要进行边界扩充维持原来的大小。
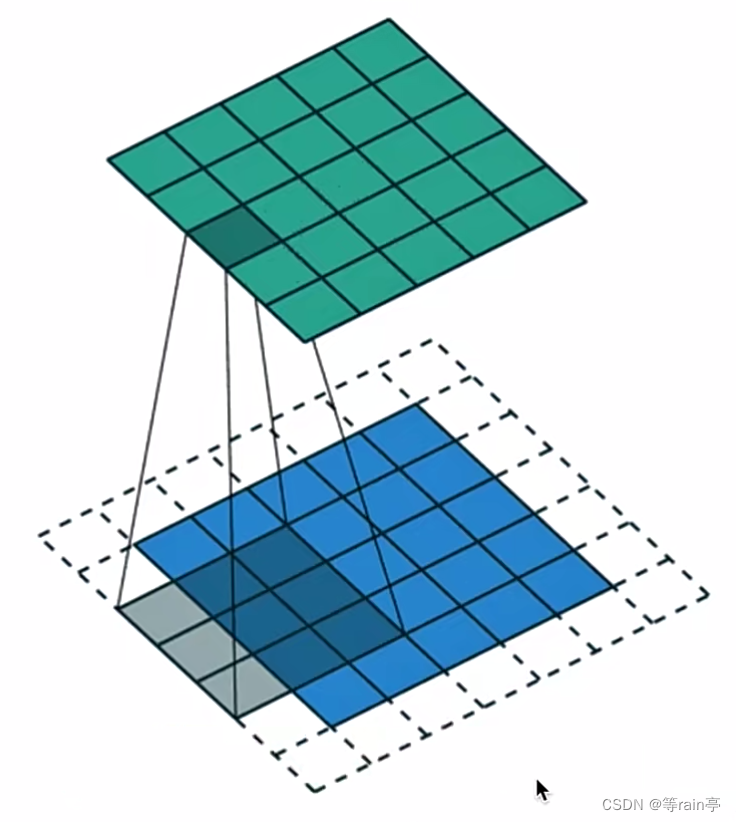
上图中下面的是原图,上面的是进行卷积后的图片,卷积核大小就是如图中的3x3,虚线部分就是进行边界扩充后的,所以很直观感受到,在进行边界扩充后才会变成原始的图像大小。

利用上述公式就可以得出不同的参数了,这对我们使用多大的卷积核,希望得到多大尺寸的图片都很有帮助。
(4)步长大小:
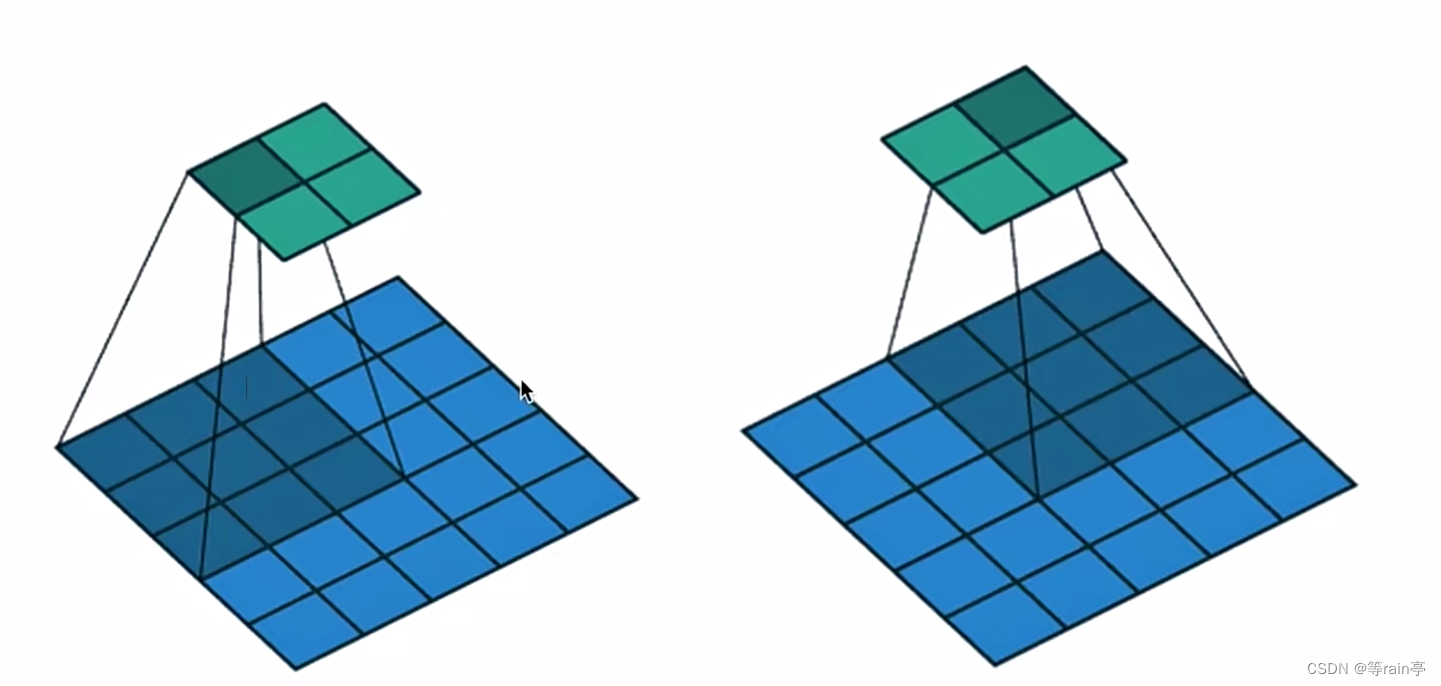
上图中的步长就是2。
低通滤波与高通滤波
低通滤波与高通滤波相关知识
低通滤波就是低于某个阈值是可以通过的
高通滤波就是高于某个阈值是可以通过的
低通滤波可以去除噪音或平滑图像(美颜中磨皮,去痘)
高通滤波可以帮助插值图像的边缘(抠图时需要边缘)
图像卷积
filter2D(src,ddepth,kernel,anchor,delta,borderType)
src:操作的原始图像
ddepth:位深,通常设置为-1
kernel:卷积核 (重要)
anchor:锚点(核的中心点)默认为-1,根据核直接去得到锚点
delta:原始图进行卷积后得到的图加上delta,默认为0
borderType:边界类型,加黑边等等 一般取默认值
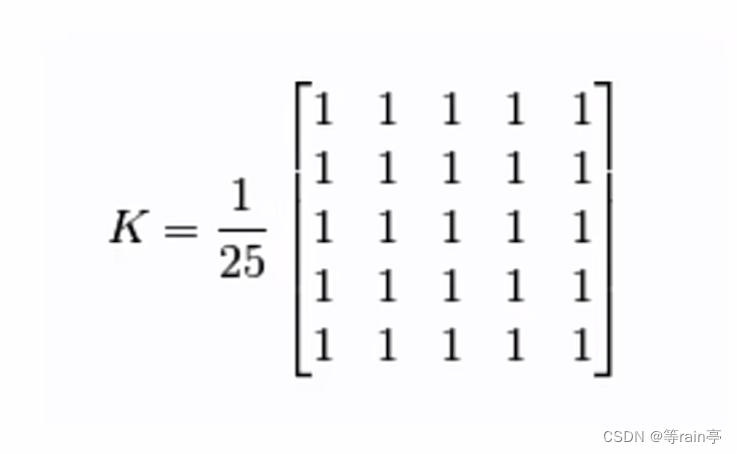
如图卷积核是上图,就意味着在原图中选5x5的像素每个值都乘1进行相加,得到的结果乘(1/25)就取得平均值,更加平滑。
图像卷积实战代码
import cv2
import numpy as npimg = cv2.imread('../MM/preview.jpg')# 自己设计的kernel的方法
kernel = np.ones((5, 5), np.float32) / 25
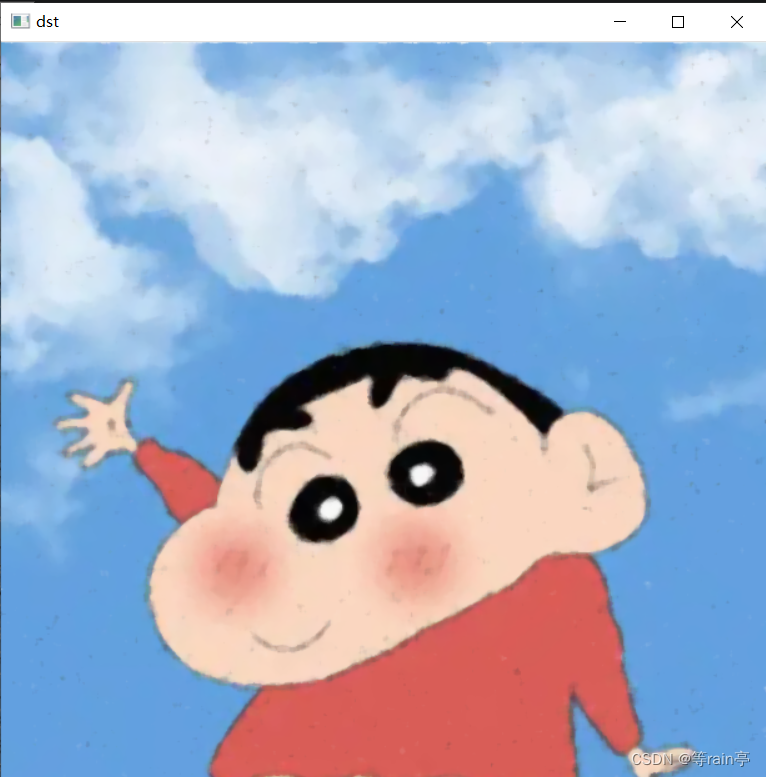
dst = cv2.filter2D(img, -1, kernel)cv2.imshow('dst', dst)
cv2.imshow('img', img)cv2.waitKey(0)

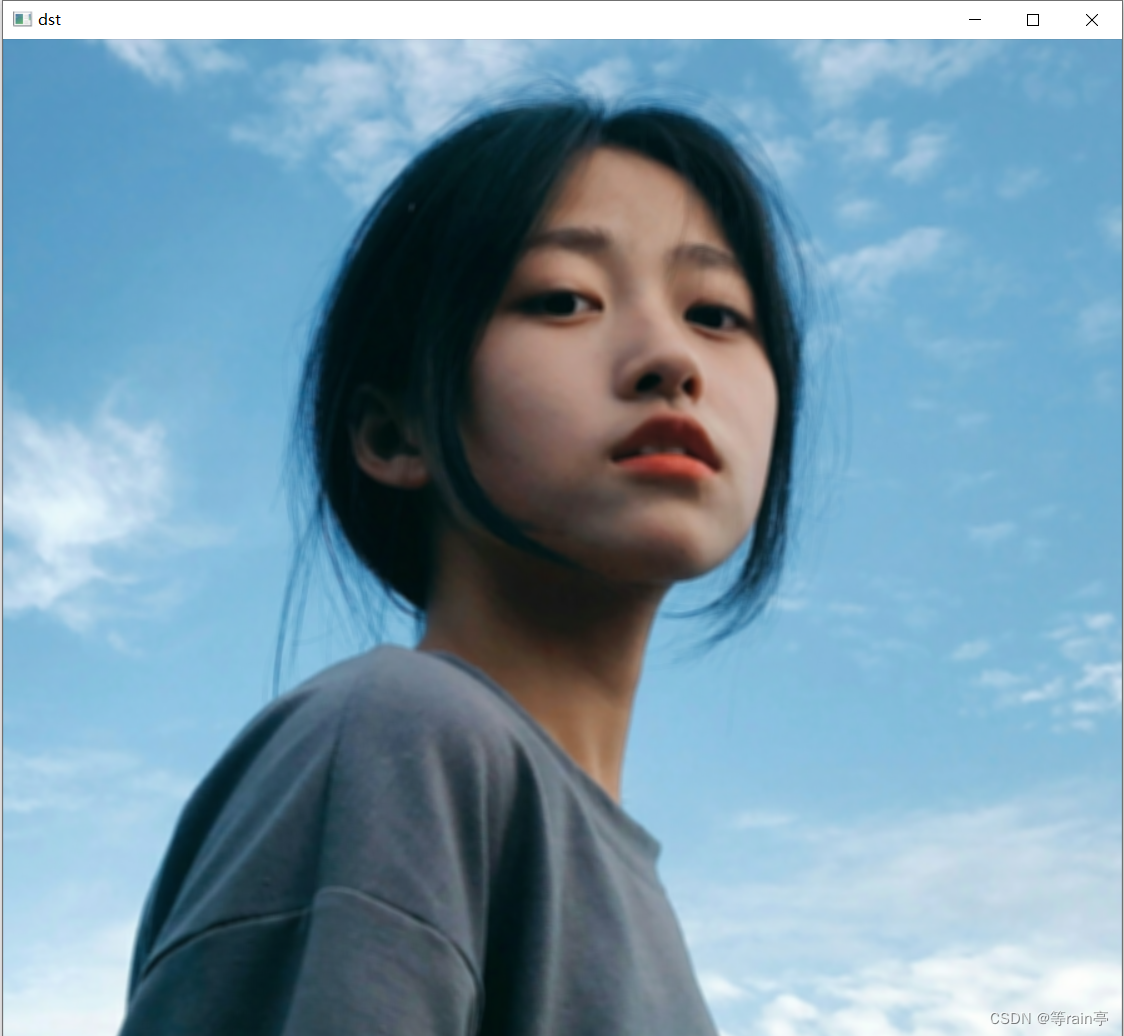
左边是原图,右边是处理后的图片。
看代码:我们设置的是5x5的全为1的矩阵,最后除25.得到结果更加平滑,但是清晰度明显下降了。(因此我们自己创的kernel往往不太合适,需要一些现存的效果较好的滤波器)
方盒滤波和均值滤波
方盒滤波:boxFilter(src,ddepth,ksize,anchor,normalize,borderType)
均值滤波:blur(src,ksize,anchor,borderType)
src:处理的图像
ddepth:位深,通常设置为-1
ksize:kernel size 卷积核大小
anchor:锚点(核的中心点)默认为-1,根据核直接去得到锚点
normalize:当normalize为True时,a=1/(W*H) 此时会退化成均值滤波
当normalize为False时,a=1 下图就是方盒滤波的卷积核
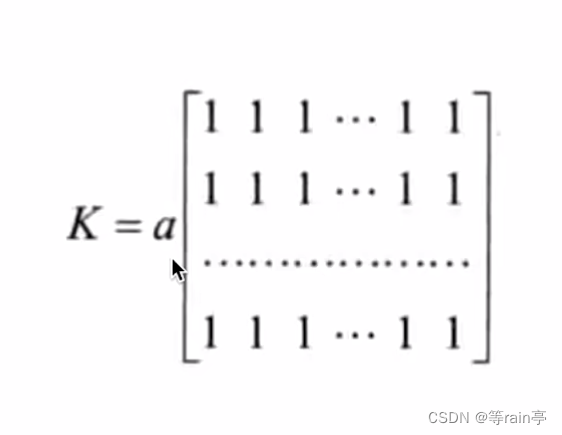
borderType:边界类型,加黑边等等 一般取默认值 。
方盒滤波和均值滤波实战代码
均值滤波:
# 均值滤波
dst = cv2.blur(img, (5, 5)) # 这个是均值滤波 用blur 其结果和自己设计kernel的结果相同结果和我们在第二部分自己设置kernel的结果相同,因为此时矩阵进行相乘后也是除25。
方盒滤波:
# 这种是方盒滤波,其初始中normalize为true变成均值滤波,如果想变成方盒滤波需要把normalize设置false
dst = cv2.boxFilter(img, -1, (5, 5), False)
dst1 = cv2.boxFilter(img, -1, (5, 5), True)
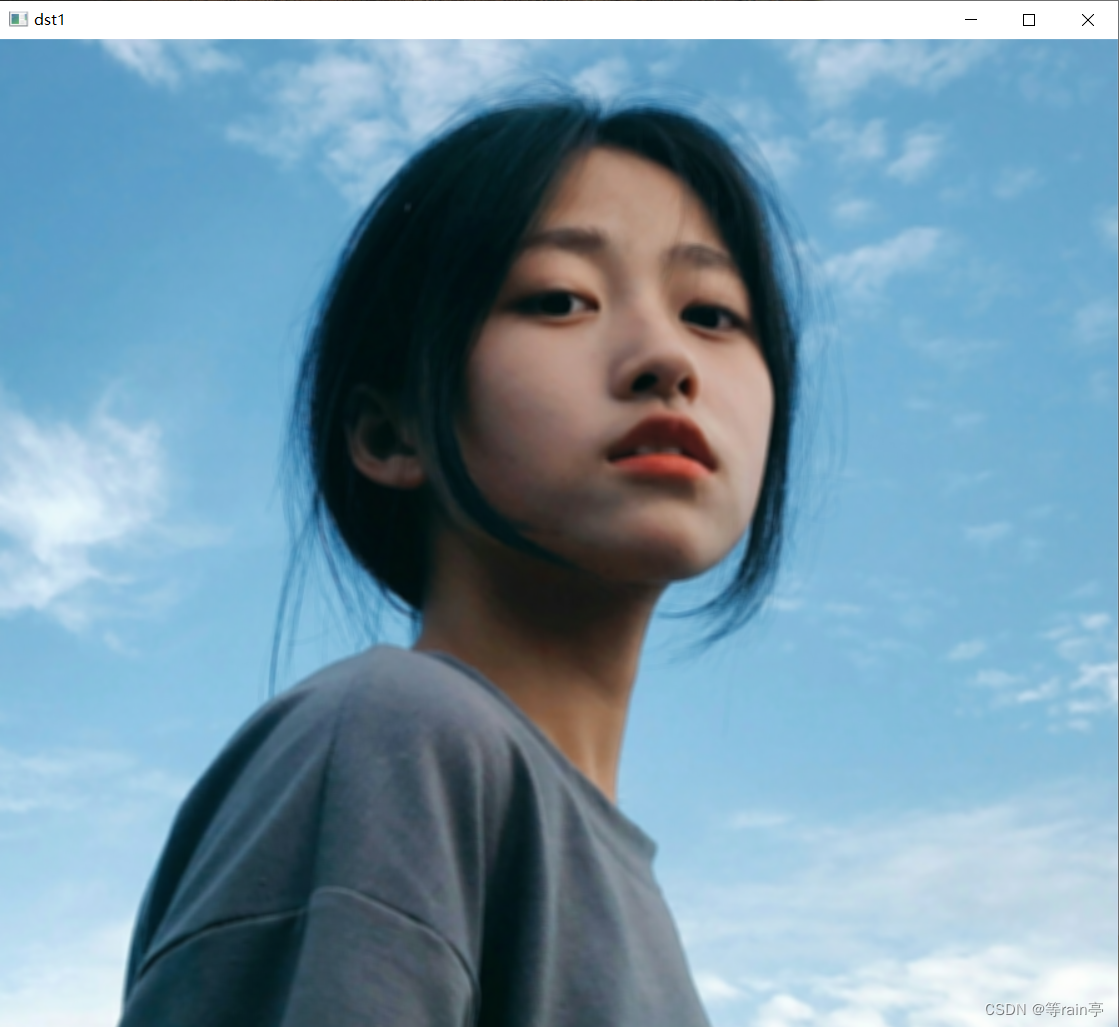
左边的是通过方盒滤波得到的结果,右边是均值滤波得到的结果。
高斯滤波
高斯滤波相关知识
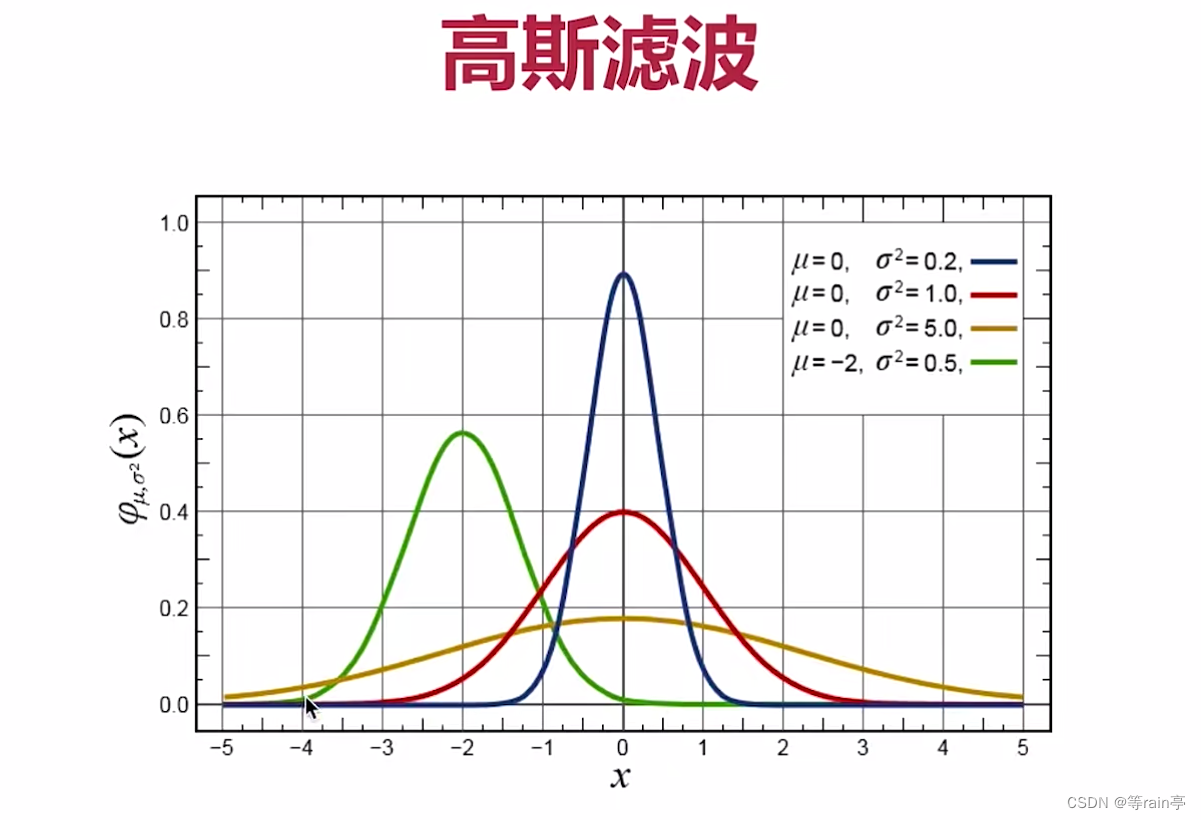
上图就是高斯滤波,发现一条曲线越靠近中间值越大(权重越大)
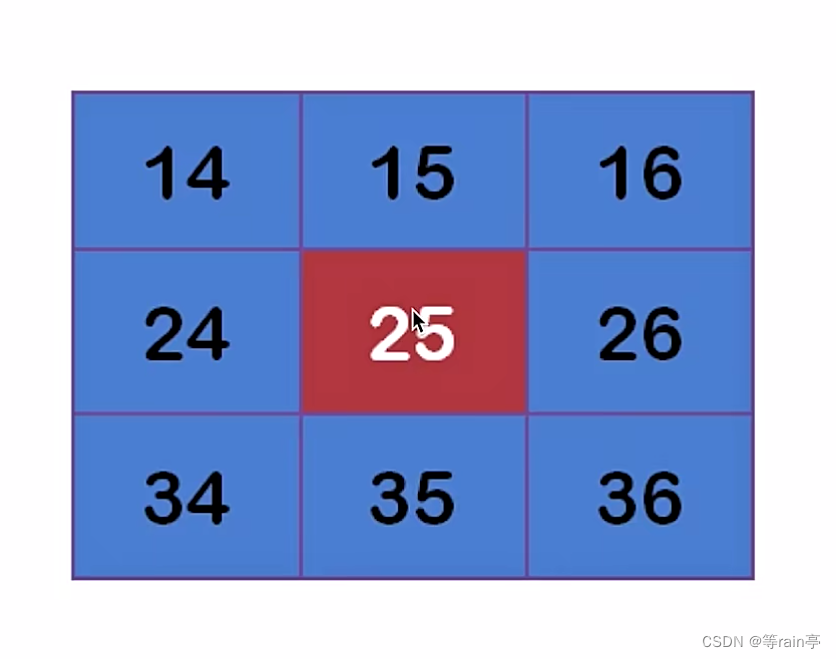
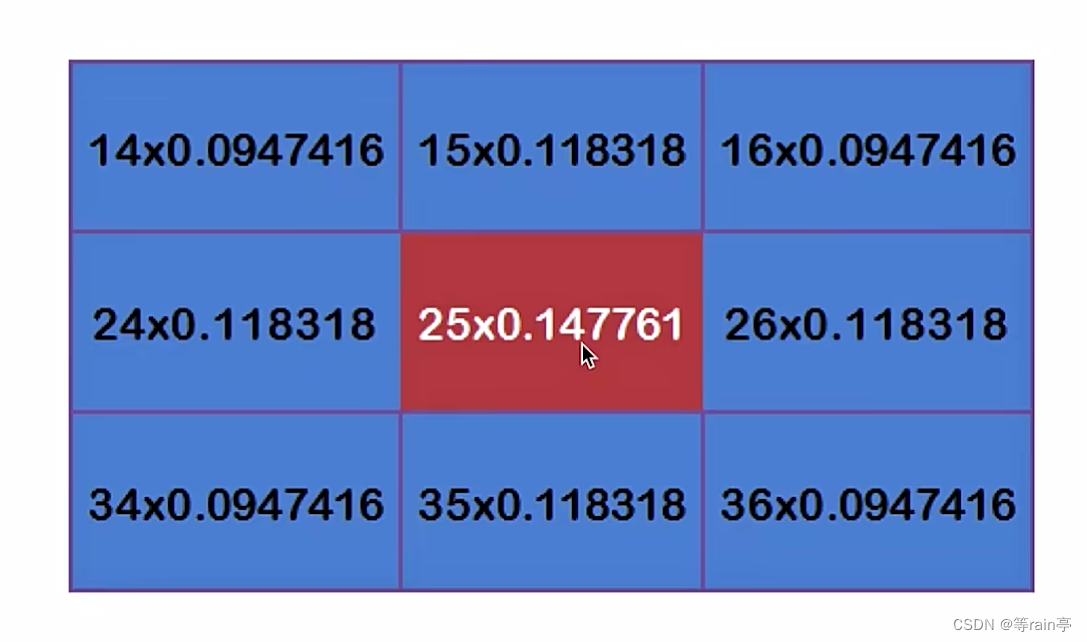
左边这张图代表的是矩阵中每个位置的大小,最中心的大小不一定是最大的(虽然第一张图25相较于周围较大), 但是最中心点的权重一定是最大的,并且越靠近中心权重越大(如第二张图,每一个数值乘一个权重的数值)
高斯滤波API:GaussianBlur(img,kernel,sigmaX,sigmaY,……)
img:需要对哪个图像进行处理
kernel:卷积核(大小) kernelsize
sigmaX,sigmaY:到中心点的延展宽度
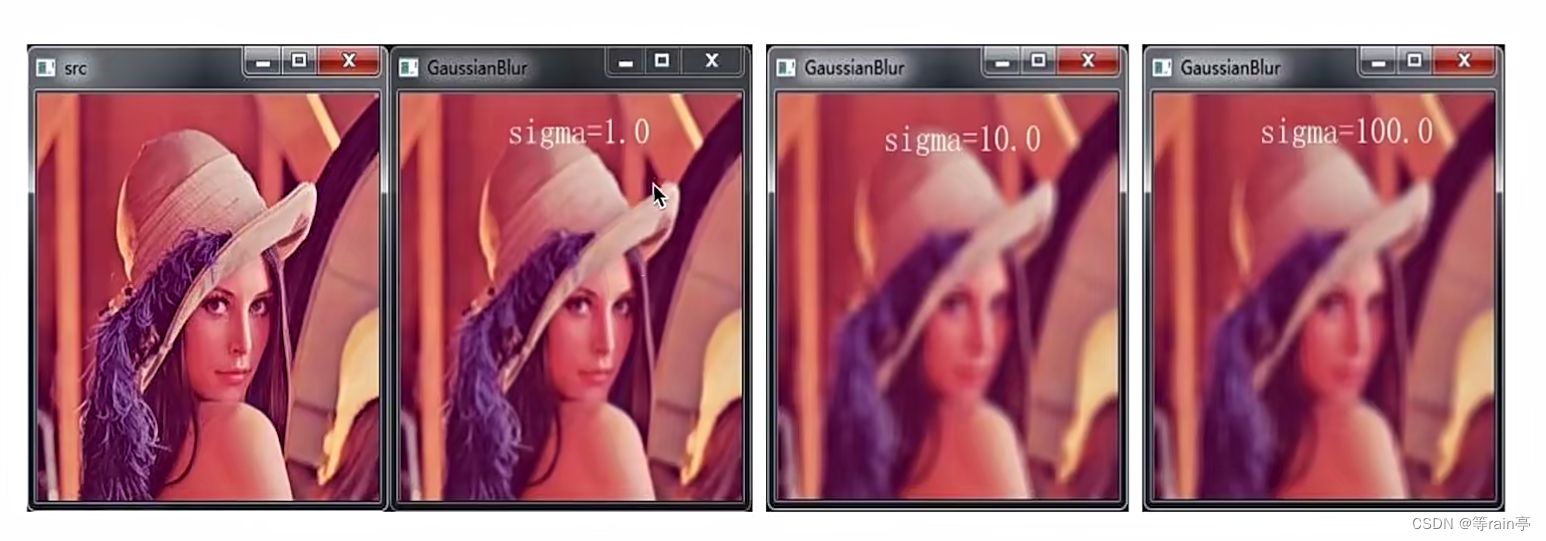
可以看出不同的sigma值的结果,如果没有sigma时,就看kernelsize,如下图。

高斯滤波实战代码
# 高斯滤波(解决高斯滤波,测量值会在均值附近产生大量的值,而离均值较远的值则会较少出现。)
# 设计中的锚点附近的权值较大
dst = cv2.GaussianBlur(img1, (5, 5), sigmaX=1)

左边是原图,发现每个环里面有很多的噪声点,经过高斯滤波后发现很多的噪声点都被去掉了,但是边缘部分也被处理掉了。(大家也可以自己去尝试改变sigma的值,看看会出现什么样的结果)
高斯滤波主要就是解决高斯噪点。
中值滤波
中值滤波相关知识
假如现在有一个数组[1556789],中值滤波就是取其中的中间值作为卷积后的结果值。
所以,当使用卷积核去卷积时,每一次都会对卷积后的结果进行排序,最后选择中间值。
中值滤波主要针对胡椒噪声(整张图像都有噪声)有很好的效果。
中值滤波API:medianBlur(img,ksize)
img:就是对哪张图片进行操作
ksize:kernelsize 卷积核的大小
中值滤波实战代码
# 中值滤波(解决胡椒噪音)
dst = cv2.medianBlur(img2, 7) 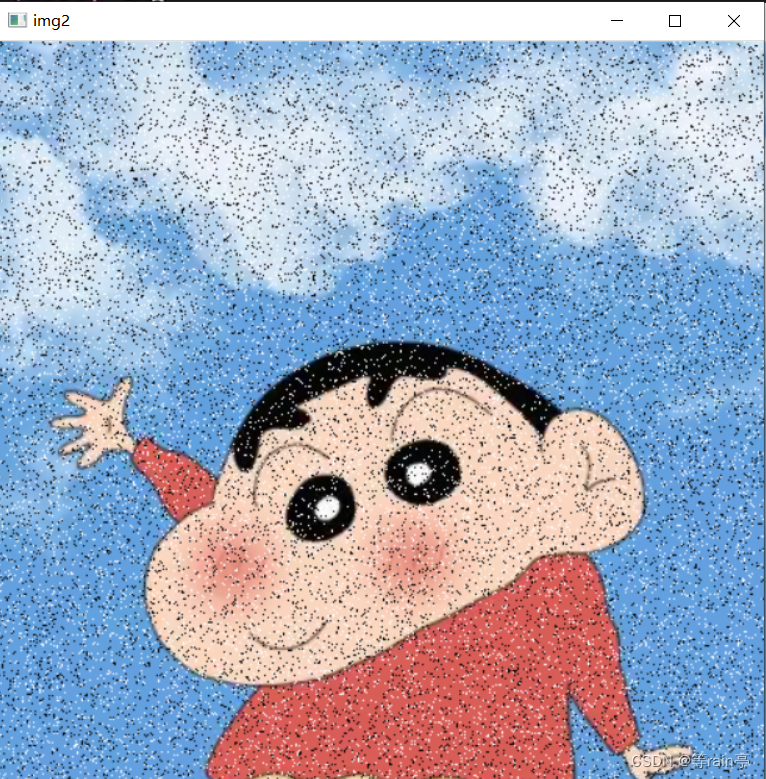
左边是具有胡椒噪声的原图,右边是处理后的图片。 但是边缘也是被弱化了。
双边滤波
双边滤波相关知识
可以保留边缘,同时对边缘内的区域进行平滑处理。(大家思考,当时我们使用高斯滤波去除区域内的高斯噪声,但是边缘被弱化了。那是否我们可以使用双边滤波解决边缘弱化的问题?)
双边滤波应用于美颜。

对于输入图像来看,边沿就是色差特别大的区域,双边滤波并没有对其进行处理,而是将边沿两边进行平滑处理。
双边滤波API:bilateralFilter(img,d,sigmaColor,sigmaSpace,……)
img:就是对哪张图片进行操作
d:直径(可以认为就是核的大小)
sigmaColor:对边沿的控制,在一定范围就不处理边沿
sigmaSpace:对边沿两边的控制,在一定范围内进行平滑处理
双边滤波实战代码
# 双边滤波(可以保留边缘,同时对边缘内的区域进行平滑处理)(主要作用是进行美颜)
dst = cv2.bilateralFilter(rita, 7, 20, 50)
# dst1=cv2.bilateralFilter(rita,20,20,50) #相比d=7,d=10磨皮效果更好

左边是原图,右边是进行双边滤波处理后的图片。大家也可以尝试去修改d等参数获得一个更好的美颜效果。
—————————————以下都是高通滤波——————————————————————
高通滤波
检测边缘
常见的高通滤波:
Sobel(索贝尔)(首先使用了高斯滤波去噪,后又一阶导,得到边沿)
Scharr(沙尔)当Sober的卷积核大小设置为-1就变成了Scharr
Sobel(索贝尔)和Scharr(沙尔)都只能对一个方向进行处理,所以得到结果后需要把x,y得到的结果加到一起
Laplacian(拉普拉斯)可以直接求出x,y方向的边缘。对于噪音比较敏感,因为内部没有降噪的处理。
大家可能这样看x,y方向的边缘不太理解,等后面实战会有所展示。
Sobel算子
Sobel算子相关知识点
先向x方向上求导,然后在y方向求导。最终结果相加。
Sobel算子API:Sobel(src,ddepth,dx,dy,ksize=3,scale=1,delta=0,borderType=BORDER_DEFAULT)
src:对哪张图进行操作
ddepth:输出图像的位深
dx=1 就检测出y边缘 dy=1就检测出x边缘
ksize:kernelsize 卷积核大小 。卷积核大小设置为-1就变成了Scharr
scale:用于缩放
delta:对结果进行加delta
borderType:边缘类型
Sobel实战代码
import cv2
import numpy as npimg = cv2.imread('../MM/chess.png')# 索贝尔算子
# y方向的边缘
y = cv2.Sobel(img, cv2.CV_64F, 1, 0, ksize=5) # 3x3的卷积核就变成了scharr# x方向的边缘
x = cv2.Sobel(img, cv2.CV_64F, 0, 1, ksize=5) # 默认ksize为3dst = x + y # python自身带的
dst1 = cv2.add(x, y)cv2.imshow('img', img)
cv2.imshow('y', y)
cv2.imshow('x', x)
cv2.imshow('dst', dst)cv2.waitKey(0)


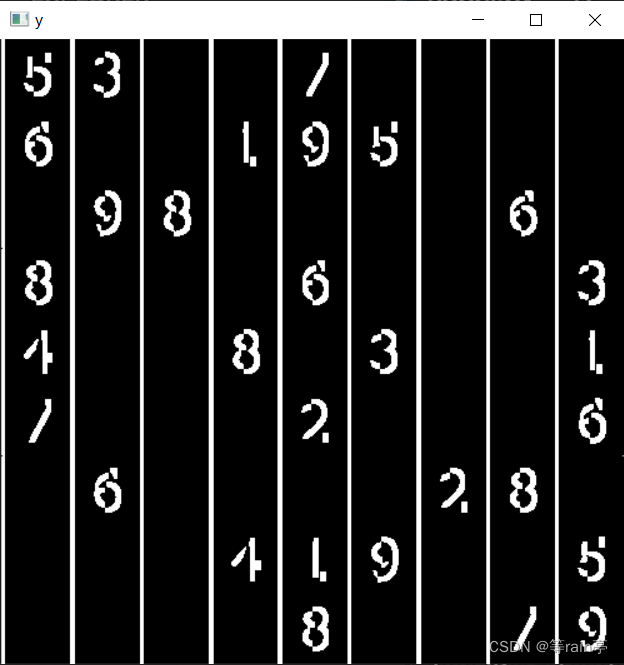

第一张图是原图,第二张代码中使dy=1,得到x方向上的边沿。第三张代码中使dx=1,得到y方向上的边沿。最后代码中的dst和dst1得到的效果都是一样的,将x,y方向上的边沿加在一起。
Sobel不可以将dx,dy都设置成1。大家可以自己设置一些看看会出现什么样的结果。
Scharr算子
Scharr算子相关知识点
与Sobel类似,但是使用的kernel值不同。Scharr只支持3x3的卷积核。
Scharr只能求x方向或y方向的边缘。
Scharr的API :Scharr(src,ddepth,dx,dy,scale=1,delta=0,borderType=BORDER_DEFAULT)
src:对哪张图进行操作
ddepth:输出图像的位深
dx=1 就检测出y边缘 dy=1就检测出x边缘
scale:用于缩放
delta:对结果进行加delta
borderType:边缘类型
Scharr算子实战代码
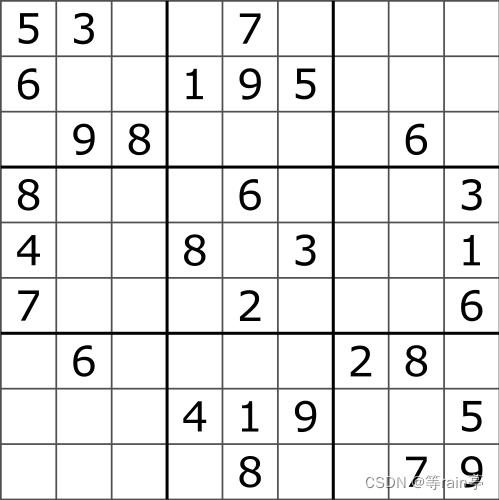



得到的图像和Sobel的图像相同。 但是Scharr还识别出来一些细小的点。(Soble用的较多)
拉普拉斯算子
拉普拉斯算子相关知识
可以同时求两个方向的边缘,不用和Sobel或Scharr一样单独求x,y。
拉普拉斯算子对于噪声比较敏感,所以一般需要进行去噪后再使用拉普拉斯。
拉普拉斯API:Laplacian(src,ddepth,ksize=1,scale=1,borderType=BORDER_DEFAULT)
src:对哪张图进行操作
ddepth:输出图像的位深
ksize=kernelsize卷积核大小
scale:用于缩放
borderType:边缘类型
拉普拉斯实战代码
ldst = cv2.Laplacian(img, cv2.CV_64F, ksize=5)


左图是原图,右图是进过拉普拉斯处理后的图片。由于原图中噪音比较少,所以直接使用了拉普拉斯。
边缘检测Canny(重要)
Canny的相关知识
对于Sobel,Scharr需要分别对x,y进行操作,拉普拉斯需要进行降噪处理。
而Canny相较于这三种就比较完美,效果好,并且简单。
canny使用的是5x5的高斯滤波消除噪声(比拉普拉斯好),计算图像梯度方向(0,45,90,135)(比Soble,Scharr全面),取局部最大值,阈值计算。
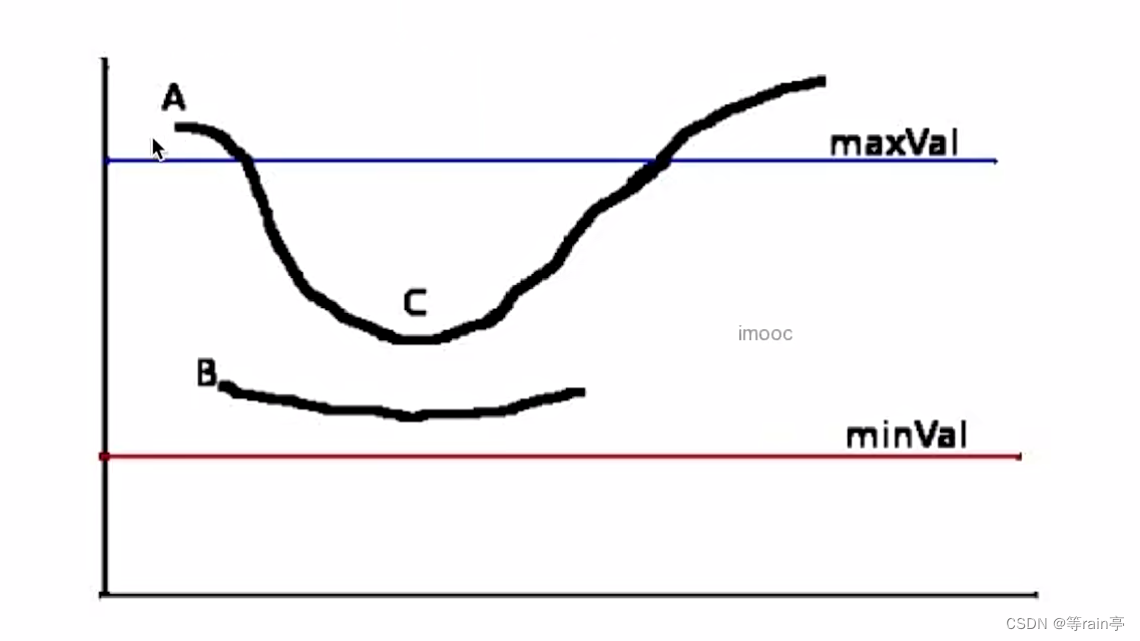
阈值计算原理,超过maxval的一定是边缘,小于minval的一定不是边缘。再maxval和minval之间的可能是可能不是,如果像c点一样于超过maxval确定是边缘的线是连续的,那c点就是边缘,否则像b一样就不是边缘。
Canny的API:Canny(img,minval,maxval,……)
img:对哪张图片进行操作
minval,maxval:要进行手动设置阈值
Canny实战代码
import cv2
import numpy as npimg = cv2.imread('../MM/preview.jpg')dst = cv2.Canny(img, 180, 200)cv2.imshow('img', img)
cv2.imshow('dst', dst)cv2.waitKey(0)
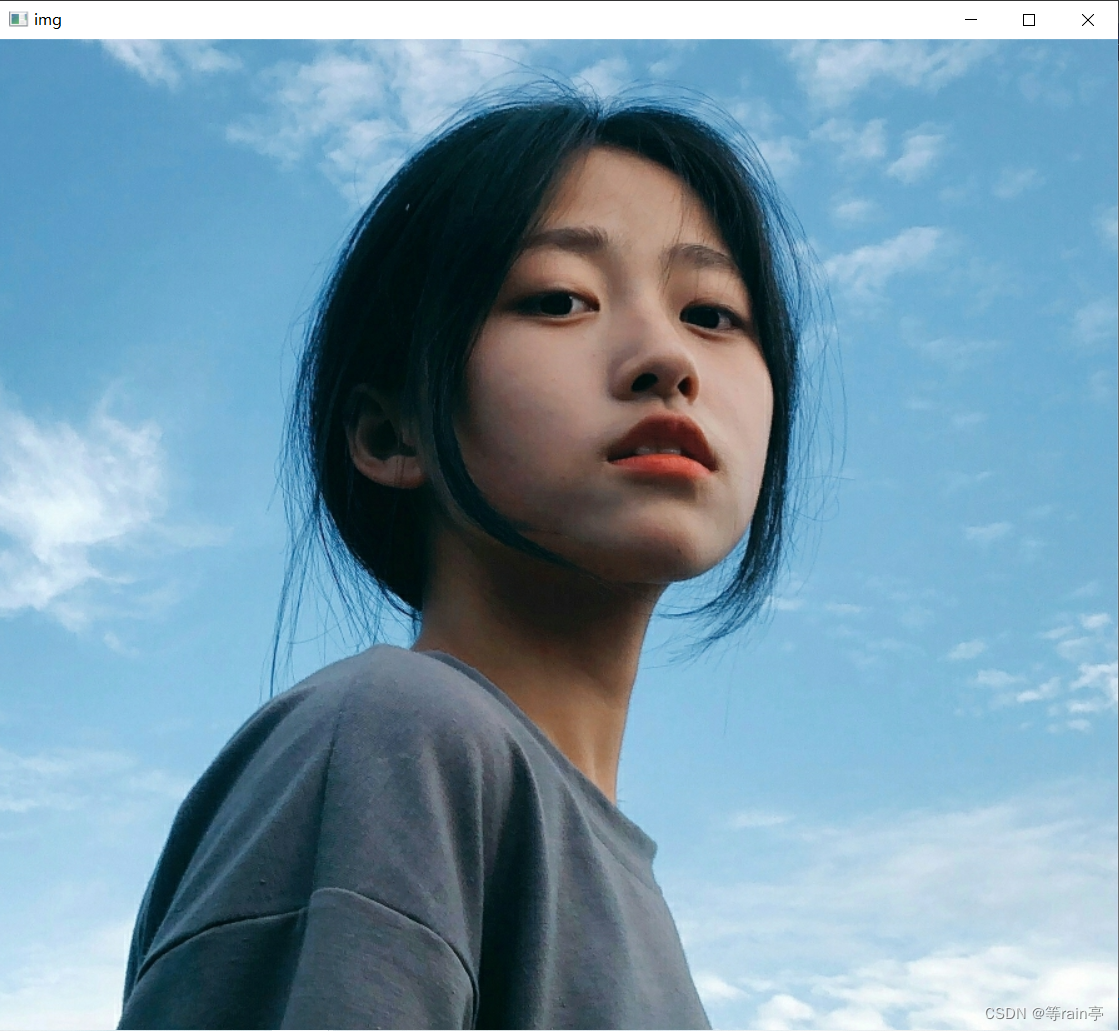
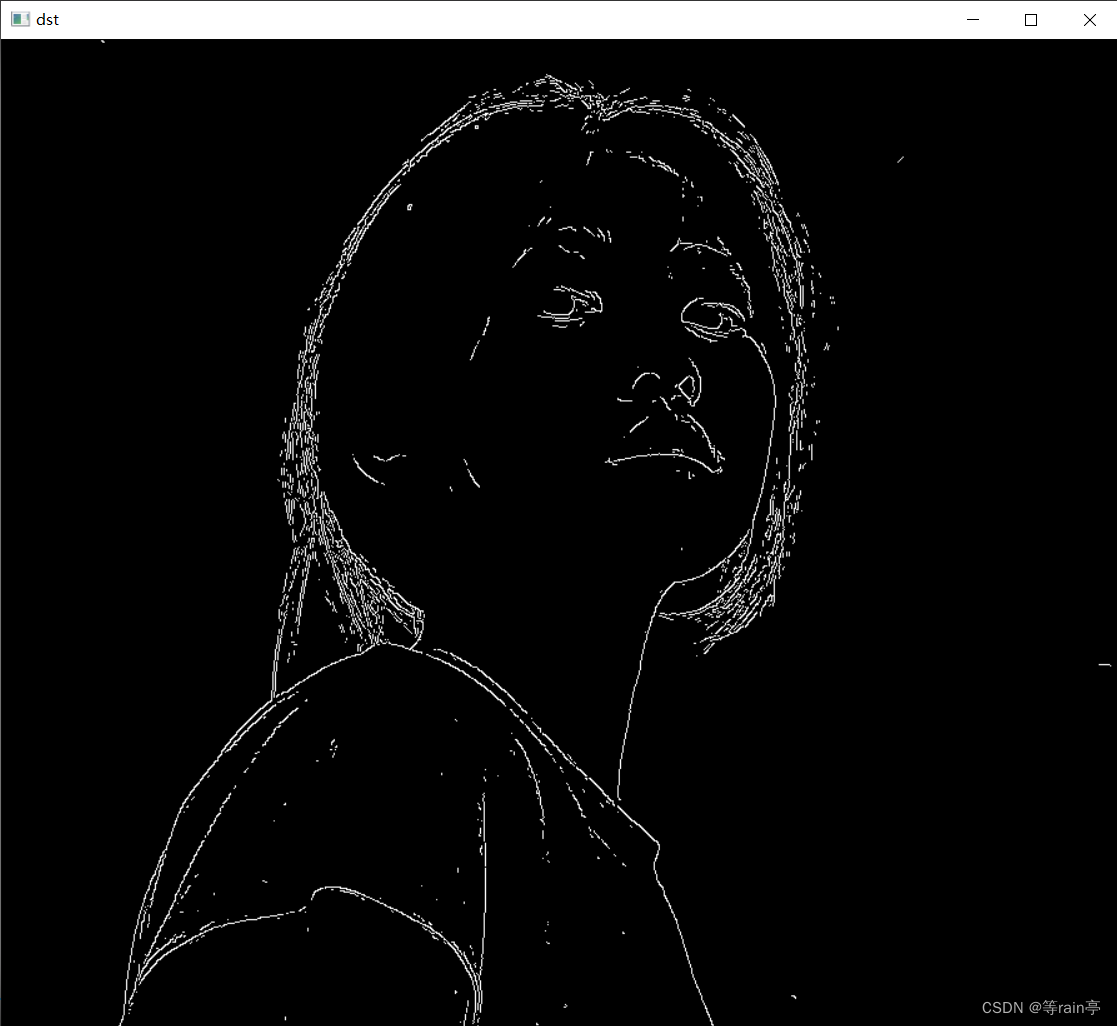
大家可以根据自己的图片改变相关的maxval和minval来体会不同的感觉。





>)


13和14题(Python))
】传统方法(直方图、图像变换)算法详解与代码实现)








![[架构之路-265]:目标系统 - 设计方法 - 软件工程 - 软件设计 - 如何做好详细设计](http://pic.xiahunao.cn/[架构之路-265]:目标系统 - 设计方法 - 软件工程 - 软件设计 - 如何做好详细设计)
