通过 随机森林 1 的介绍,相信大家对随机森林都有了一个初步的认知,知道了随机和森林分别指的是什么,以及决策树根据什么选择内部节点。本文将会从森林深入到树,去看一下决策树是如何构建的。网上很多文章都讲了决策树如何构建,但在我看来不够生动形象,不够深入,希望此文能够让你彻彻底底了解决策树以及公式的含义。
一、决策树的核心与逻辑
决策树的核心是确定节点用哪个特征当做判断条件,优先选择分类效果最强的特征当做节点的判断条件。构建决策树的逻辑也就清晰了,根节点选择分类效果最强的特征当做判断标准,后面的节点依次选择剩余特征中分类最强的特征当做判断标准,如果两个一样强,那就形成分支,最终构建成一棵树。
二、衡量特征分类效果强弱的指标
随进森林和决策树构建的逻辑我们已经非常清楚了,我们只要知道如何判断判断特征分类效果的强弱就可以一通百顺。这里我们会讲四个指标,分别是信息熵、信息增益、信息增益率和基尼指数。
2.1 信息熵
熵大家应该都听说过,熵是用来衡量混乱程度的指标,越有序,熵越小,也可以理解为纯度的指标,越纯,熵越小。
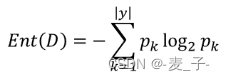

Ent(D)表示样本集合 D 的信息熵;![]() 表示 k 类样本所占的比例;所以信息熵就是计算每个类别
表示 k 类样本所占的比例;所以信息熵就是计算每个类别![]() 的累加;
的累加;
因为0<![]() <1,所以
<1,所以![]() 越接近 1, 也就是 k 的概率接近 1,
越接近 1, 也就是 k 的概率接近 1,![]() 越接近 0,熵越小;相反 k 的概率越小,熵越大。举个极端的例子:假如只有一个类别,那么这个类别的概率肯定是 1,非常纯,非常有序,熵也达到了最小值 0。
越接近 0,熵越小;相反 k 的概率越小,熵越大。举个极端的例子:假如只有一个类别,那么这个类别的概率肯定是 1,非常纯,非常有序,熵也达到了最小值 0。
这里延伸一下为什么很多公式都带 log,本质是为了让差值小的两个数字经过 log 计算后,让差值更明显。在这里因为概率之间的差异非常小,可能差异在 0.1 甚至 0.01,计算以 2 为底的,0.01 和 0.02 的对数, 结果分别时-6.644和-5.644,差异增加了 100 倍。
2.2 信息增益
我们知道了熵可以描述一个集合的纯度,那么如何利用熵来决定节点选择哪个特征划分呢?这里就引入了信息增益的概念,信息增益表示的是熵减少的程度。划分逻辑就是,划分后每个集合的熵乘以该集合占总集合的比例,然后求和与划分前熵相比较,减少的多说明划分效果好。

Gain(D,a)表示特征 a 对数据 D 进行划分所获得的信息增益,Ent(D) 表示划分前的信息熵, 表示划分后的信息熵。v 表示的是特征a第 v 个取值,
表示划分后的信息熵。v 表示的是特征a第 v 个取值, 表示样本 D 在v上的样本集合,
![]() 就是样本 D 在 v 上的样本集合占 D 整个集合的权重。
就是样本 D 在 v 上的样本集合占 D 整个集合的权重。
举个例子,集合 A 为[1,1,1,2,2,2],经过特征 X 划分为 集合 B1[1,1,2,2] 和集合 B2[1,2],经过特征 Y 划分为集合 C1[1,1,1] 和集合 C2[2,2,2]。
- 集合A 的熵
=1;
- 集合B1和 B2 的熵一样
=1,再乘以每个集合占总集合的比例 1*(4/6) + 1*(2/6) = 1;
- 集合 C1 和 C2 的熵一样都是 0,乘以每个集合占总集合的比例依然是 0;
- Gain(A,X)=0,Gain(A,Y)=1;
由此可见,通过特征 X 划分,熵依然是1,信息增益为 0,没有减小;通过特征 Y 的划分,熵从1 变成 0,信息增益为 1。很明显特征 Y 划分效果好,所以选择 Y 当做该节点划分特征。
每个节点都可以使用这个方法确定特征,从根节点不断向下延伸,这样就形成一个决策树,使用信息增益确认节点特征的代表算法时 ID3。
2.3 信息增益率
通过信息增益构建决策树有个致命的缺点,更喜欢用有大量取值的特征来分类,可能会陷入太过关注细节,无法看到大局的情况。举个例子:假设你正在构建一个决策树来帮助你预测明天是否会下雨。你有很多数据,包括每天的温度、湿度、风速等信息。其中一个特征是"云朵的形状",因为每天的云朵都可能有微小的变化,每个云朵形状只对应一个结果,导致用云朵的形状分类信息增益最小,但实际上明天是否下雨和云朵形状关系很小,甚至没有关系,这就是典型的在训练数据上表现很好,但实际使用很差,鲁棒性很差。
针对上面这种情况,有人就提出了用信息增益率来代替信息增益。信息增益率多了一个衡量本身属性分散程度的指标作为分母。


表示数据集 D 的样本量,
表示数据集 D 在特征第v上的样本数量。
如果数量特别小,占整个数据集的比例就特别小,把负号给到 log,log 计算出来的值就越大,结合右边的 log 图来看,
占整个数据集的比例越小,斜率越大,log 增长速度远大于
![]() ,所以整体来看,IV(a)越大。更通俗点的理解就是,特征 a 的可能取值数目越多,IV(a)越大,信息增益率越小。这样通过增加 IV(a)分母,很好的牵制了信息增益偏向取值更多的特征的问题。
,所以整体来看,IV(a)越大。更通俗点的理解就是,特征 a 的可能取值数目越多,IV(a)越大,信息增益率越小。这样通过增加 IV(a)分母,很好的牵制了信息增益偏向取值更多的特征的问题。
2.4 基尼指数
基尼指数和熵差不多,都是用来衡量集合的纯度,基尼指数越小,表示数据越纯。
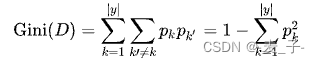
表示第 k 类的数据占总数据的比例;
表示随机抽取的样本既属于类别 k,又再次抽取时仍然属于类别 k 的概率,可以理解为连抽两次都是 k;
如果一个数据集特别纯,那么 的概率比较高,
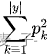 较大,基尼指数最终结果较小。决策树会选择最小基尼指数的特征来划分。
较大,基尼指数最终结果较小。决策树会选择最小基尼指数的特征来划分。
基尼指数与信息增益率相比,有哪些进步呢?
1 、信息增益率为了避免信息增益的致命缺点,会优先考虑样本数量少的特征,具有偏向性,而基尼系数没有这个偏向性;
2 、计算开销更少,没有涉及到 log 的计算;
)



(1/3))
)









——基于PIC16F877A的温度光照检测装置的protues仿真)



