目录1.斐波那契数列：

2.青蛙跳台阶问题：

3.汉诺塔问题

---

1.斐波那契数列：

由斐波那契数列从第三项开始，每一项等于前两项之和，可以使用递归计算给定整数的斐波那契数。 

  1，1，2，3，5，8，13，21，34，55… 

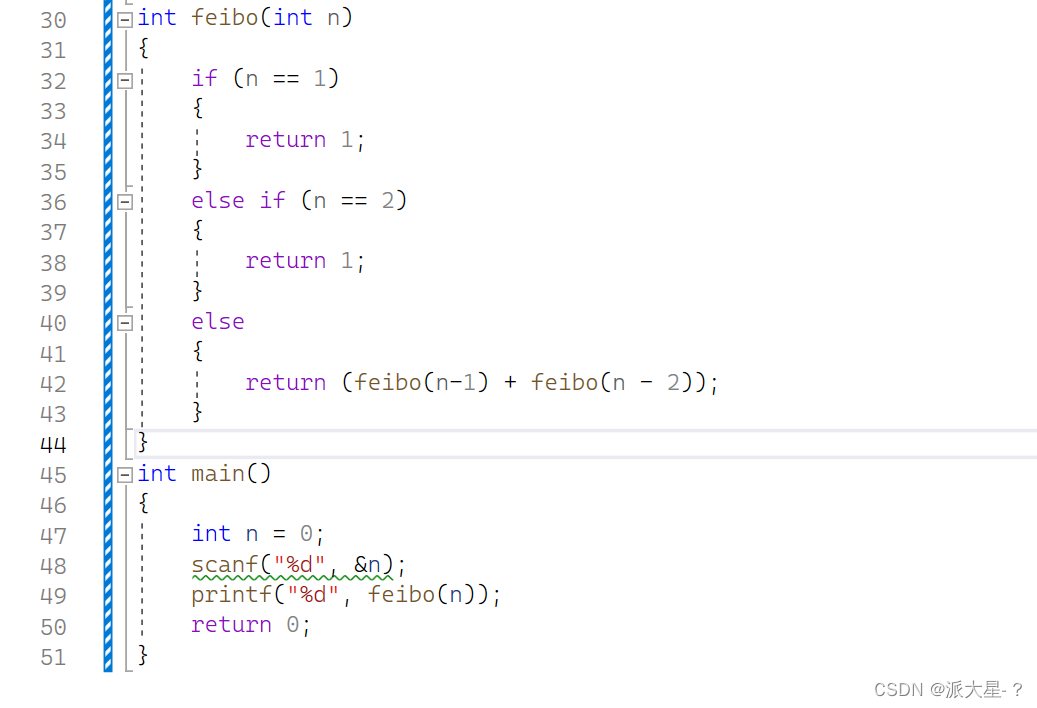
分析：

从第三项开始，当前项为前两项之和。

注意终止条件有两个n=1，n=2项，

如果n>=3，则进入42行循环，一直自我调用。

2.青蛙跳台阶问题：

题目：从前有一只青蛙他想跳台阶，有n级台阶，青蛙一次可以跳1级台阶，也可以跳2级台阶；问：该青蛙跳到第n级台阶一共有多少种跳法

分析：

刚刚看完这个题目感觉还是有些懵的，但是不能慌我们要一步一步分析找规律。

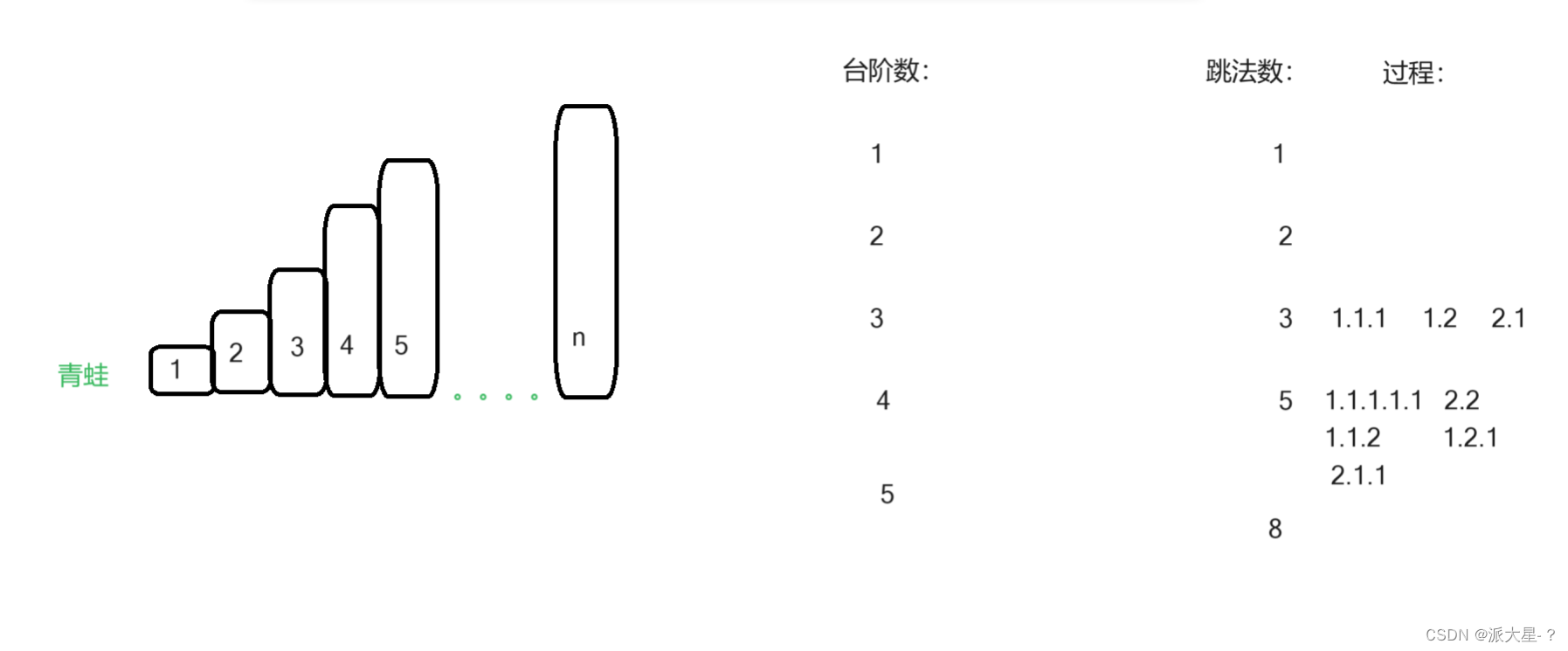
再分析前三步时，我们好像以为规律是步数就是台阶数等于跳法数，但分析到n=5时，却不一样了。它真正的规律是从第三项开始跳法数等于前一步的跳法数加上前前一步的跳法数。

如何快速得到当前所求的步数？

当n=5时，它一次要么跳一个要么跳两个，

当它跳一个跳向1台阶，还剩下4个台阶，以当前台阶为新起点跳4完个台阶有5种方法，

当它跳两个台阶跳向2台阶，还剩下3个台阶，以第二个台阶为新起点跳完3个台阶有3中方法。

所以跳完5个台阶一共有3+5种方法，

这就是引用了动态规划：用上一步的结果快速计算下一步的结果。

细心的你发现它不就是一个隐藏的斐波那契数列吗！！！

3.汉诺塔问题

题目描述 n个圆盘从下面开始按大小顺序摆放在A柱子上。 并且规定，任何时候，在小圆盘上都不能放大圆盘，且在三根柱子之间一次只能移动一个圆盘，求最少的移动步骤。

分析：

题目要我们求出n个盘子从A柱移动到C柱所需的最少步骤，这题明显是种找规律题目。

所以我们应该先不要慌张，从n为1开始分析，多多分析发现规律。

n=1：

可以直接从A盘移动到C盘不需要经过B盘。这时只需要1步；

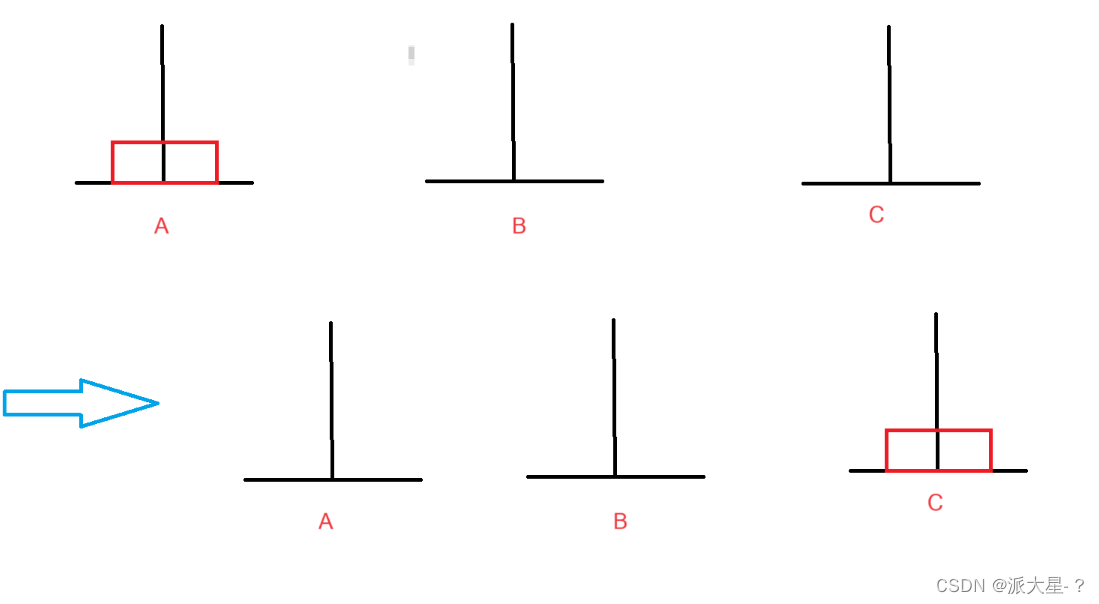
n=2：

分析：第一步’A-->B‘

           第二步’A-->C‘

           第三步’B-->C‘

           一共需要三步

n=3：

 一共需要七步

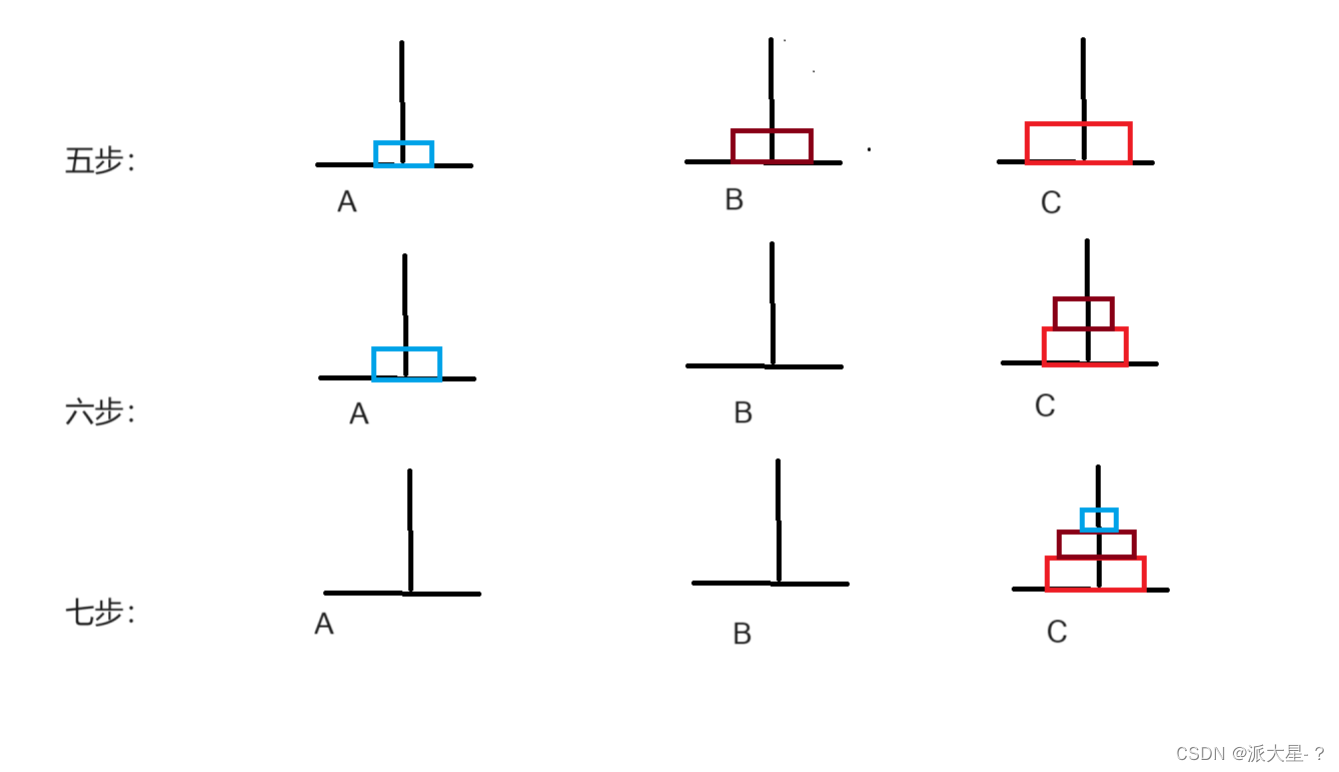
分析：这里好像我们已经发现一个规律，最小步数=2^n-1;

如果n无限大，那么我们是不是可以用分割的思想，将n分为1和n-1;

这时采用递归的方法，递归的终止条件为 n=1

在柱间移动的代码：

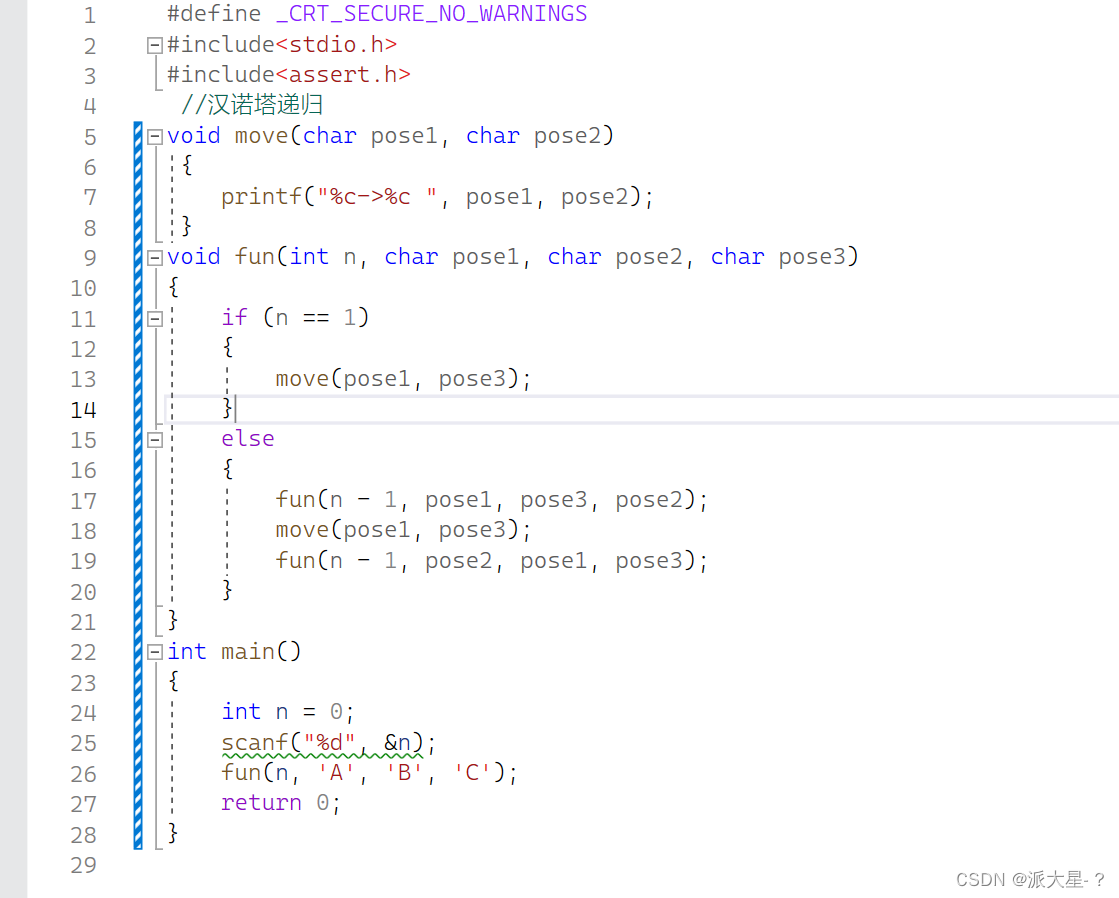
分析：

move函数作用来打印 起始位置 到 停留的位置；

fun函数表示每个盘子在ABC三个柱间移动的过程；A：起始柱，B：转移盘，C：目标盘

n为盘子的个数，pose1表示A柱，pose2表示B柱，pose3表示C柱；

代码思路是将盘子分为：1和n-1，

17行：将n-1个盘子从A通过C柱移动到B柱；

18h行：move打印最后一个盘子从A柱移动到C柱；

也就是一开始n个盘子，n！=1，进入fun（n-1，pose1，pose2，pose3）

在 fun（n-1，pose1，pose2，pose3）中，(n-1)!=1,

再进入fun（n-2，pose1，pose2，pose3）

一直地推……

直到n=1，然后回归

递归终止条件为n=1时，只剩下一个盘子就是最底下那个最大的。将此盘直接从A盘-->C盘；

此时n-1个盘子在B柱，在19行，再调用fun函数，将n-1个盘子从B柱通过A柱移动到C柱，任务完成。