老老规矩,看目录,平均每年2E,跟2D一样,D是全对,E是全错,侧面也看出10道题,大概是3A/B,3C,2D,2E,其实还是蛮平均的。但E为1道的情况居多。
第20题如果要硬猜,要不就是留给E吧

再把其他年份的第20题找出来,选了A或D,也就是说,第20题,验证了A的有效性,无效,就直接选E,有效,就还得验证B,B有效,就选D。

最后,第20题是分水岭,前面除了第17题,其他不大可能选E。即第20题之前若判断A,B都不充分,那么就选C。或者就把所有感觉要联立都选C,从C中找E,哈哈,不过这个概率说不定更低。
文章目录
- 2023
- 真题(2023-20)-E-不要被选项迷惑,不是取值范围,是两个不同未知数;-选项特点:一个大于号,一个小于号,两个未知数;
- 真题(2023-21)-E-选项特点:两个已知X的值;
- 2022
- 真题(2022-20)-E;选项特点-一个已知,一个只有;
- 真题(2022-23)-E-容易误判C,因为【一个等号+一个不等号】
- 2021
- 真题(2021-17)-E-要不要联立-要联立选C;(我爱说实话)两个条件看起来确实很像需要联立的样子
- 真题(2021-23)-E-易误判选C,因为【一个不等号,一个等号】
- 2020
- 真题(2020-20)-E
- 真题(2020-22)-E-条件轮换对称+结论要求具体某个量(不对称)-条件未知量轮换对称:轮换对称:a→b→c→d轮换位置后条件表达式不变;很容易误选C,因为【一个等号+一个不等号】
- 2019
- 真题(2019-22)-E选项蒙猜-特别难的结论就直接过;(我爱说实话,这个第一眼也像可以联合)
- 2018
- 真题(2018-21)-E;(我爱说实话,这个第一眼也像可以联合)
- 2017
- 真题(2017-20)-E;选项特点:两个已知X的值(这个特点没啥用,因为ABCD都出现)
- 2016
- 真题(2016-20)-E-看起来好像联合可以出答案的样子
- 2015
- 真题(2015-20)-E-看起来好像联合可以出答案的样子;-选项特点:和等式,积等式。
- 2014
- 2013
- 真题(2013-17)-E-特别难的结论选E(我爱说实话,考试想不到这个点);选E选项往往不需要联合,联合的选C的几率高
选E选项(条件1和条件2单独都不充分,联合起来也不充分)
对学员的掌握程度要求更高
判断误差的罪魁祸首,是E,在不确定的情况下,宁愿把E选成别的选项,也不要把别的选项选成E。
1.往往不需要复杂的推理或计算。通过特殊反例,常识,逻辑关系可看出来。
2.选E选项往往不需要联合,联合的选C的几率高。
真题:2013年17题;2012年21题;
自从13年出现“可确定”型题目,E选项绝大部分出自此类题目
1.特别难的结论就直接过;
真题:19年22题,13年01,17题
2.不满足“要啥给啥”原则:
(1)条件(比例关系)与所求结论(具体量)信息类型不匹配;
(2)条件(范围)与所求结论(具体量)信息类型不匹配;
真题:13年10月20题(缺少相关年份真题)
3.条件轮换对称+结论要求具体某个量(不对称)
条件未知量轮换对称;轮换对称:a→b→c→d轮换位置后条件表达式不变;
真题:20年22题。
2023
真题(2023-20)-E-不要被选项迷惑,不是取值范围,是两个不同未知数;-选项特点:一个大于号,一个小于号,两个未知数;
-几何-解析几何;
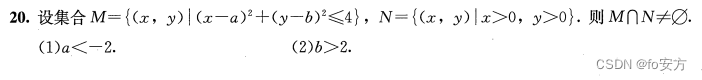

真题(2023-21)-E-选项特点:两个已知X的值;
-应用题-路程


2022
真题(2022-20)-E;选项特点-一个已知,一个只有;
-简单算术题
20.将 75 名学生分成 25 组,每组 3 人,则能确定女生人数。
(1)已知全是男生的组数和全是女生的组数。
(2)只有1男的组和只有1女的组数相等。

真题(2022-23)-E-容易误判C,因为【一个等号+一个不等号】
-数列-等比数列-等比中项;+一元二次函数
23.已知𝑎,𝑏为实数,则能确定𝑎的值。
(1)𝑎,𝑏,𝑎 + 𝑏成等比数列。
(2)𝑎(𝑎 + 𝑏) > 0。

2021
真题(2021-17)-E-要不要联立-要联立选C;(我爱说实话)两个条件看起来确实很像需要联立的样子
-应用题-工程
17.清理一块场地,则甲乙丙三人能在2天内完成。
(1)甲乙两人需要3天完成。
(2)甲丙两人需要4天完成。

真题(2021-23)-E-易误判选C,因为【一个不等号,一个等号】
-应用题-路程
23.某人开车去上班,有一段路因维修限速通行,则可以算出此人上班的距离。
(1)路上比平时多用了半小时。
(2)已知维修路段的通行速度。

2020
真题(2020-20)-E
-代数-方程-出现了两个及以上未知量,而数量关系却少于未知量的个数-整数不定方程-先根据题目转化为ax+by=c形式的不定方程,然后结合整除、倍数和奇偶特征分析讨论求解
20、共有n 辆车,则能确定人数。
(1)若每辆车 20 座,1 车未满。
(2)若每辆车 12 座,则少 10 个座。


真题(2020-22)-E-条件轮换对称+结论要求具体某个量(不对称)-条件未知量轮换对称:轮换对称:a→b→c→d轮换位置后条件表达式不变;很容易误选C,因为【一个等号+一个不等号】
-E-代数-方程-出现了两个及以上未知量,而数量关系却少于未知量的个数-整数不定方程-先根据题目转化为ax+by=c形式的不定方程,然后结合整除、倍数和奇偶特征分析讨论求解
22、已知甲、乙、丙三人共捐款 3500 元,则能确定每人的捐款金额。
(1)三人的捐款金额各不相同。
(2)三人的捐款金额都是 500 的倍数。



2019
真题(2019-22)-E选项蒙猜-特别难的结论就直接过;(我爱说实话,这个第一眼也像可以联合)
-E-算术-整除
22、设 n 为正整数,则能确定n 除以 5 的余数。
(1) 已知 n 除以 2 的余数。
(2) 已知n 除以 3 的余数。


2018
真题(2018-21)-E;(我爱说实话,这个第一眼也像可以联合)
-应用题-简单算术
21.甲购买了若干件 A 玩具,乙购买了若干件 B 玩具送给幼儿园,甲比乙少花了 100 元,则能确定甲购买的玩具件数。
(1)甲与乙共购买了 50 件玩具。
(2)A 玩具的价格是 B 玩具的 2 倍。

E。本题考查方程组相关知识。假设甲的玩具价格为每件x元,共买了A件,乙的玩具价格为每件y元,共买了B件,题干前提条件为Ax+100=By,其中,x,y,A,B均为未知数。条件(1)为A+B=50 ,条件(2)为x=2y,显然,无论条件(1)、(2)单独,还是联合,未知数个数都多于方程个数,无唯一解,不能确定未知数A的值,都不充分。


2017
真题(2017-20)-E;选项特点:两个已知X的值(这个特点没啥用,因为ABCD都出现)
-比例应用题-增长率
20.能确定某企业产值的月平均增长率。
(1)已知一月份的产值。
(2)已知全年的总产值答案。


答案应该是E。(否则2017年没有选E)
首先理解“月平均增长率x”:只与第一个月和最后一个月的产值有关。如:一月a、二、三、四…十一、十二月3a: a ( 1 + x ) 11 = 3 a a(1+x)^{11}=3a a(1+x)11=3a,得 ( 1 + x ) 11 = 3 (1+x)^{11}=3 (1+x)11=3,得: x = 3 11 − 1 x=\sqrt[11]{3}-1 x=113−1
∴(2)全年总产值是无关的。更改为“12月的产值”,才选C。
2016
真题(2016-20)-E-看起来好像联合可以出答案的样子
-应用题-溶液
20.将 2 升甲酒精和 1 升乙酒精混合,得到丙酒精,则能确定甲、乙两种酒精的浓度。
(1)1 升甲酒精和 5 升乙酒精混合后的浓度是丙酒精浓度的 1 2 \frac{1}{2} 21倍。
(2)1 升甲酒精和 2 升乙酒精混合后的中毒是丙酒精浓度的 2 3 \frac{2}{3} 32倍。

2015
真题(2015-20)-E-看起来好像联合可以出答案的样子;-选项特点:和等式,积等式。
-数列-等差数列
20.设{ a n a_n an}是等差数列,则能确定数列{ a n a_n an}
(1) a 1 + a 6 = 0 a_1+a_6=0 a1+a6=0
(2) a 1 a 6 = − 1 a_1a_6=-1 a1a6=−1

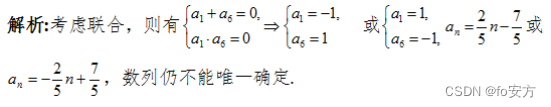
2014
我14年没有E,没人来管管的吗
2013
真题(2013-17)-E-特别难的结论选E(我爱说实话,考试想不到这个点);选E选项往往不需要联合,联合的选C的几率高
-E-算术-质合数
17. p = m q + 1 p = mq + 1 p=mq+1为质数。
(1) m m m为正整数, q q q为质数。
(2) m , q m,q m,q均为质数。





数据格式的兼容问题)


)

算法做题步骤分析)




覆盖优化 - 附代码)
)


)

