BM61 矩阵最长递增路径

题目矩阵最长递增路径

给定一个 n 行 m 列矩阵 matrix ，矩阵内所有数均为非负整数。你需要在矩阵中找到一条最长路径，使这条路径上的元素是递增的。并输出这条最长路径的长度。这个路径必须满足以下条件： 1. 对于每个单元格，你可以往上，下，左，右四个方向移动。你不能在对角线方向上移动或移动到边界外。 2. 你不能走重复的单元格。即每个格子最多只能走一次。数据范围：，进阶：空间复杂度，时间复杂度例如：当输入为[[1,2,3],[4,5,6],[7,8,9]]时，对应的输出为5，其中的一条最长递增路径如下图所示：
示例1
输入
[[1,2,3],[4,5,6],[7,8,9]]
输出
5
说明
1->2->3->6->9即可。当然这种递增路径不是唯一的。
示例2
输入
[[1,2],[4,3]]
输出
4
说明
1->2->3->4

备注:
矩阵的长和宽均不大于1000，矩阵内每个数不大于1000
在这里插入图片描述

BM61 矩阵最长递增路径

该题是牛客网基础算法题递61题。

暴力探索：

根据题意是每个坐标点在上下左右方向可增量延伸的最长路径。如果能够记录每个坐标点，在每个坐标探索一遍可能生成的路径，最后取最长的那条，就是每个坐标的最长路径。最后提示时间超时了，只能解到第二组就超时了。

/*** 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可** 递增路径的最大长度* @param matrix int整型二维数组 描述矩阵的每个数* @return int整型*/
export function solve(matrix: number[][]): number {// write code hereconst result = {}const backupStack = []matrix.forEach((arr, y) => {arr.forEach((val, x) => {backupStack.push({ x, y })})})const computed = (value: number, key: string) => {if (Array.isArray(result[key])) {const maxVal = Math.max(...result[key])if (value > maxVal) {result[key].push(value)}} else {result[key] = [value]}}const callback = (y: number, x: number, key: string) => {if (matrix[y] && matrix[y][x]) {const value = matrix[y][x]computed(value, key)// leftif (matrix[y] && matrix[y][x] < matrix[y][x - 1]) {callback(y, x - 1, key)}// rightif ( matrix[y] && matrix[y][x] < matrix[y][x + 1]) {callback(y, x + 1, key)}// topif (matrix[y - 1] && matrix[y][x] < matrix[y - 1][x]) {callback(y - 1, x, key)}// bottomif (matrix[y + 1] && matrix[y][x] < matrix[y + 1][x]) {callback(y + 1, x, key)}}}while (backupStack.length > 0) {const item = backupStack.shift()if (item) {const { x, y } = itemconst key = `${y}-${x}`callback(y, x, key)}}const getLength = () => {const list: number[][] = Object.values(result)return Math.max(...(list.map(arr => arr.length)))}return getLength()
}

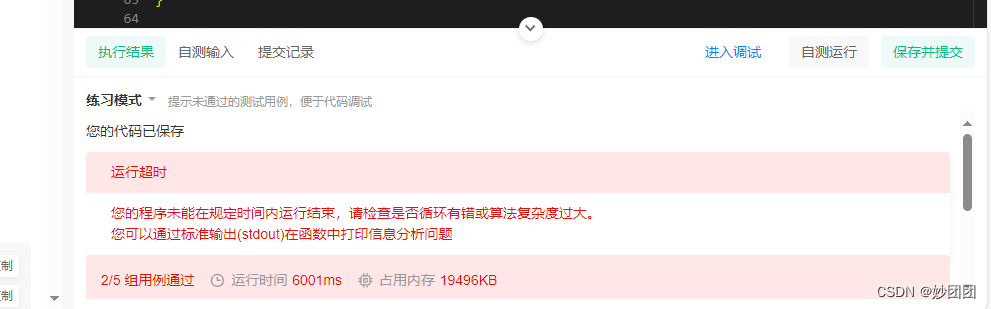
在这里插入图片描述

理论上足够覅人时间和空间是可以解出来的，实践上在该题的要求下，时间是不满足的。

不再二次探索相同的地方.

通过观察发现其中已经探索过的节点其实不需要在继续探索了，只需要拿到已经探索过的点的最长路径就可以了，如果该节点还没有被遍历探索那么继续探索，直到走完所有节点
细节注意：因为每个方向都要判断有没路径，所以需要判断边界，只能在没有超出数据边界的情况下进行。

/*** 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可** 递增路径的最大长度* @param matrix int整型二维数组 描述矩阵的每个数* @return int整型*/
export function solve(matrix: number[][]): number {// write code hereconst resultMap = matrix.slice(0, matrix.length).map(arr => arr.map(_ => 0))const dfs = (y, x) => {if (resultMap[y][x] > 0) {return resultMap[y][x]}if (resultMap[y][x] === 0) {resultMap[y][x] = 1}const direction = [[y + 1, x],[y - 1, x],[y, x - 1],[y, x + 1]]direction.forEach(([nextY, nextX], k) => {const yL = matrix.lengthconst xL = matrix[y].lengthif ((nextY >= 0 && nextY < yL) &&(nextX >= 0 && nextX < xL) &&(matrix[y][x] < matrix[nextY][nextX])) {resultMap[y][x] = Math.max(resultMap[y][x], dfs(nextY, nextX) + 1)}})return resultMap[y][x]}const getMaxLen = () => {let num = 0matrix.forEach((arr, y) => {arr.forEach((_, x) => {num = Math.max(num, dfs(y, x))})})return num}return getMaxLen()
}