参考
Reinforcement Learning, Second Edition
An Introduction
By Richard S. Sutton and Andrew G. Barto
无模型方法
在前面的文章中,我们介绍的是有模型方法(Model-Based)。在强化学习中,"Model"可以理解为算法对环境的一种建模与抽象。这个模型用于捕捉智能体与环境之间的交互关系。建模的目的是为了帮助智能体更好地理解环境的动态特性,从而能够更有效地制定策略。在 Model-Based 方法中,智能体使用这个模型来规划未来的行动,而在 无模型方法(Model-Free) 方法中,智能体直接通过与环境的交互来学习策略,而不依赖于显式的环境模型。
无模型方法仅仅需要从环境中收集到 S , A , R , . . . S,A,R,... S,A,R,... 序列,作为算法的经验,持续更新。
根据每一次采样序列的长短,无模型方法分为 MC 和 TD 两大类。
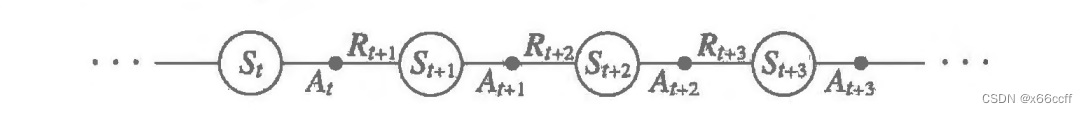
MC 蒙特卡洛方法
从一个状态 s s s出发,重复采样多条轨迹,每一条状态都采样直到终止状态,把轨迹的平均折扣回报作为状态价值的估计
V π ( s ) = E [ G t ∣ s ] ≈ 1 N ∑ i = 1 N G t i V_\pi (s)=\mathbb{E}[G_t|s]\approx \frac{1}{N}\sum_{i=1}^N G_{t}^i Vπ(s)=E[Gt∣s]≈N1i=1∑NGti

MC 的增量更新
V π ( s ) ← V π ( s ) + 1 N ( G t − V π ( s ) ) V_\pi(s) \leftarrow V_\pi(s)+\frac{1}{N}(G_t-V_\pi(s)) Vπ(s)←Vπ(s)+N1(Gt−Vπ(s))
对于非平稳问题,增量更新为(红色:TD target):
V π ( s ) ← V π ( s ) + α ( G t − V π ( s ) ) V_\pi(s) \leftarrow V_\pi(s)+\alpha(\red{G_t}-V_\pi(s)) Vπ(s)←Vπ(s)+α(Gt−Vπ(s))
缺点:
- 只适用于有限幕问题
- 更新慢,需要采样整条序列,然后才进行更新。
TD 时序差分方法
TD 在 MC 上做了修改,不需要采样整条序列,而是只采样一步(贝尔曼方程),用 V V V 对后面所有的奖励进行估计(自举法) ,然后立刻进行更新(红色:TD target):
V π ( s ) ← V π ( s ) + α ( R t + 1 + γ V π ( S t + 1 ) − V π ( s ) ) V_\pi(s) \leftarrow V_\pi(s)+\alpha(\red{R_{t+1}+\gamma V_\pi(S_{t+1})} -V_\pi(s)) Vπ(s)←Vπ(s)+α(Rt+1+γVπ(St+1)−Vπ(s))
一般来说,TD方法比MC方法收敛更快。
MC vs TD
- TD 可以在线学习,效率高一些,采样和学习可以同时进行,而MC不行,要一直模拟到游戏结束
- TD 方差大,因为没训练好的时候 V V V本身就估计不准,所以 V t + 1 V_{t+1} Vt+1引入了额外的误差
强化学习中的重要性加权
例子引入:现在给定的轨迹是另一个策略 μ \mu μ (顶级选手的下法 μ ( a ∣ s ) \mu(a|s) μ(a∣s))采样出来的,如果用 μ \mu μ 的轨迹计算得到的 G t G_t Gt (经验)直接用来进行另一个策略 π \pi π (入门选手 π ( a ∣ s ) \pi(a|s) π(a∣s))的学习,那么就可能不合适。
从算法的角度说,在于 TD target G t G_{t} Gt 对于 μ \mu μ 的评价是不准确的,我们需要对 G t G_t Gt进行修正。
改进的方法是使用重要性加权。
- MC 的重要性加权
朴素的想法:对于那些 π \pi π 也能做出类似的 ( a ∣ s ) (a|s) (a∣s) 动作,给予这些动作对应的轨迹的回报 G t G_t Gt 更大的权重,反之给予小的权重。
于是 MC 的重要性加权如下:
G t π / μ = π ( a t ∣ s t ) μ ( a t ∣ s t ) π ( a t + 1 ∣ s t + 1 ) μ ( a t + 1 ∣ s t + 1 ) . . . π ( a T ∣ s T ) μ ( a T ∣ s T ) G t G_{t}^{\pi/\mu}=\frac{\pi(a_t|s_t)}{\mu(a_t|s_t)}\frac{\pi(a_{t+1}|s_{t+1})}{\mu(a_{t+1}|s_{t+1})}...\frac{\pi(a_{T}|s_{T})}{\mu(a_{T}|s_{T})}G_t Gtπ/μ=μ(at∣st)π(at∣st)μ(at+1∣st+1)π(at+1∣st+1)...μ(aT∣sT)π(aT∣sT)Gt
用加权之后的总折扣 G t π / μ G_{t}^{\pi/\mu} Gtπ/μ更新值函数
V π ( s ) ← V π ( s ) + α ( G t π / μ − V π ( s ) ) V_\pi(s) \leftarrow V_\pi(s)+\alpha(G_{t}^{\pi/\mu}-V_\pi(s)) Vπ(s)←Vπ(s)+α(Gtπ/μ−Vπ(s))
问题在于:
- 无法在 μ \mu μ 为0时使用
- 由于连续多个商相乘,显著增大方差。
改进:- TD 的重要性加权
TD 由于只用一步进行更新,所以相应的重要性采样只有一个商,可以降低方差。
V π ( s ) ← V π ( s ) + α ( π ( a t ∣ s t ) μ ( a t ∣ s t ) ( r t + 1 + γ V ( S t + 1 ) ) − V π ( s ) ) V_\pi(s) \leftarrow V_\pi(s)+\alpha \left(\blue{\frac{\pi(a_t|s_t)}{\mu(a_t|s_t)}}\red{(r_{t+1}+\gamma V(S_{t+1}))}-V_\pi(s) \right) Vπ(s)←Vπ(s)+α(μ(at∣st)π(at∣st)(rt+1+γV(St+1))−Vπ(s))

TD 方法: SARSA
两个步骤:
- ϵ \epsilon ϵ-贪心(或者 Decaying ϵ − \epsilon- ϵ−贪心,更加有效)地选择 A A A,从而得到 S , A , R ′ , S ′ , A ′ S ,A ,R' ,S', A' S,A,R′,S′,A′五元组,
- 利用五元组更新价值函数,TD target = R + γ Q ( S ′ , A ′ ) =R+\gamma Q(S',A') =R+γQ(S′,A′)
Q ( S , A ) ← Q ( S , A ) + α [ R + γ Q ( S ′ , A ′ ) − Q ( S , A ) ] Q(S,A)\leftarrow Q(S,A) + \alpha [\red{R+ \gamma Q(S',A')} - Q(S,A)] Q(S,A)←Q(S,A)+α[R+γQ(S′,A′)−Q(S,A)]
SARSA 是一种 On-policy (同轨策略)方法,因为用于计算 TD target 的值函数和用于动作选择的值函数是同一个。
特点:
- 同轨策略
- 运算量小,轻量化,在线
- 偏保守,考虑了 ϵ \epsilon ϵ 的影响(悬崖例子)
TD 方法:Q-learning
和 SARSA 的唯一区别:
将给 TD target 加了一个 max,是用最大估计价值来更新值函数。
Q ( S , A ) ← Q ( S , A ) + α [ R + γ max a Q ( S ′ , a ) − Q ( S , A ) ] Q(S,A)\leftarrow Q(S,A) + \alpha [\red{R+ \gamma \max_a Q(S',a)} - Q(S,A)] Q(S,A)←Q(S,A)+α[R+γamaxQ(S′,a)−Q(S,A)]
- 异轨策略(Off-policy)
- 运算量大,因为要比较每一个 a a a 的价值
- 偏激进,没有考虑 ϵ \epsilon ϵ 的影响(悬崖例子)
- 有过估计的问题,由于 max \max max 操作,会让估计值偏大,导致算法过于自信。
SARSA 改进: 期望 SARSA
由于 SARSA 每一次只用 S ′ , A ′ S',A' S′,A′作为下一个状态的估计,会导致方差较大, 期望 SARSA 引入后继所有状态价值的期望,降低了方差。
Q ( S , A ) ← Q ( S , A ) + α [ R + γ ∑ a π ( a ∣ S ′ ) Q ( S ′ , a ) − Q ( S , A ) ] Q(S,A)\leftarrow Q(S,A) + \alpha [\red{R+ \gamma \sum_{a} \pi(a|S')Q(S',a)} - Q(S,A)] Q(S,A)←Q(S,A)+α[R+γa∑π(a∣S′)Q(S′,a)−Q(S,A)]
期望 SARSA 既可以看作 SARSA 的期望版本,也可以看作将 Q-learning 的 max 改为 mean 的版本。
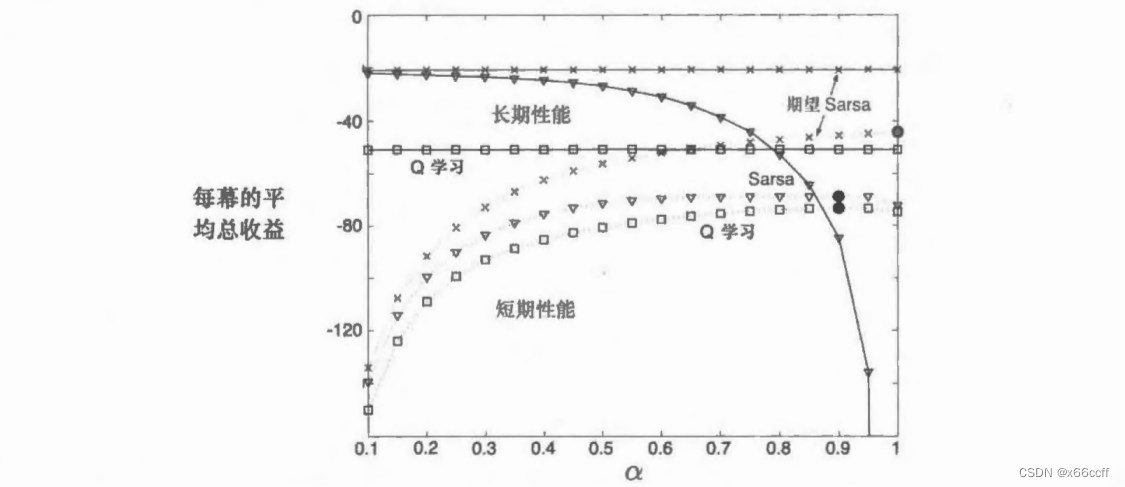
期望 Sarsa 在计算上比 Sarsa 更加复杂。但作为回报,它消除了因为随机选择产生的方差。 在相同数量的经验下,我们可能会预想它的表现能略好于 Sarsa, 期望 Sarsa也确实表现更好。
除了增加少许的计算量之。期望 Sarsa 应该完全优于这两种更知名的时序差分控制算法
最大化偏差与双学习
Q-learning 存在最大化偏差的问题,max 的操作会让算法过高估计值函数。
书中的例子:
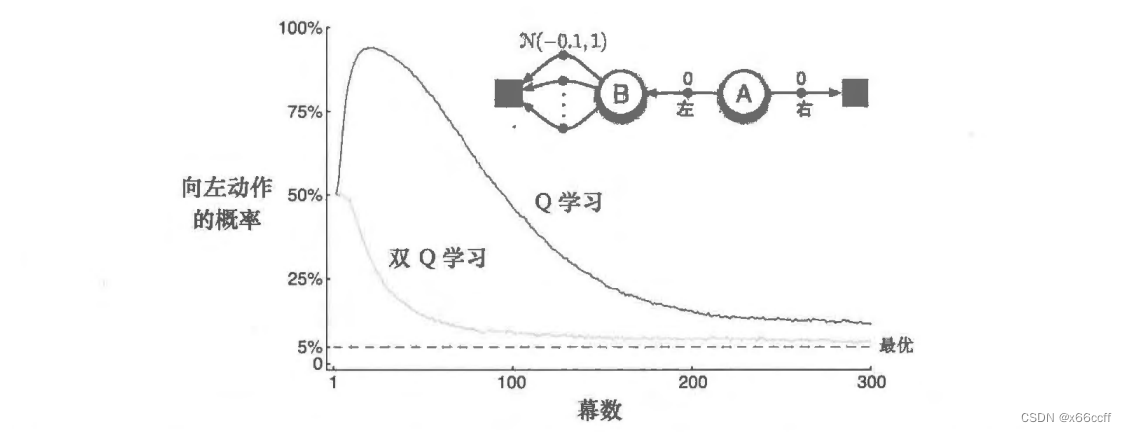
走左边在期望意义上是更差的,但是由于左边的奖励是由 N ( − 0.1 , 1 ) \mathcal{N}(-0.1,1) N(−0.1,1) 产生的,在刚开始的时候算法的 Q ( s , a ) Q(s,a) Q(s,a) 大概率有正数,因此 max 之后会得到一个正数,这会驱使算法在刚开始的时候往左边走。当估计次数增多之后,左边各个状态都收敛到 -0.1 的均值奖励,从而 max Q 必然小于0,算法开始回头,往期望恒为 0 的右边走。
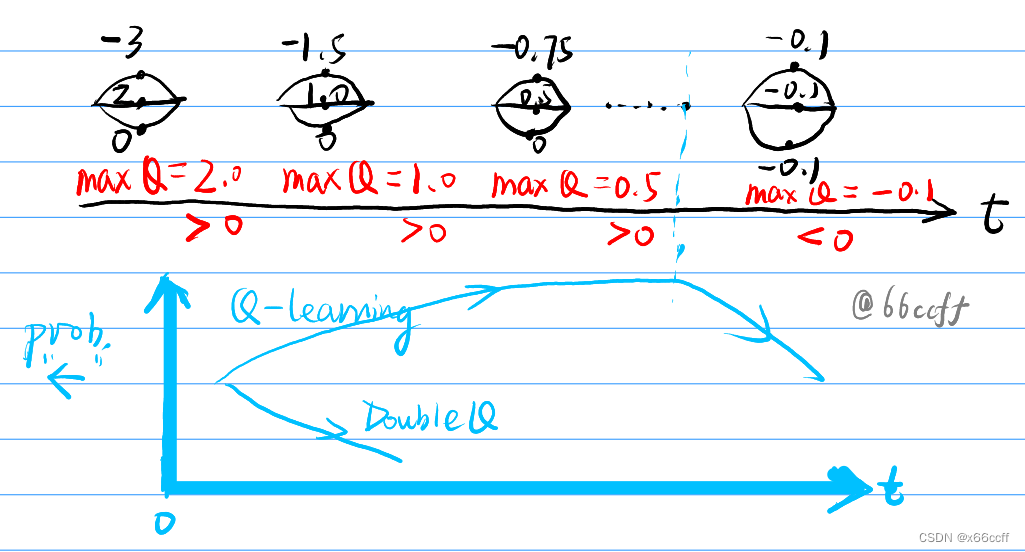
双 Q 学习
这里实际上是非深度版本的Double Q-learning,因为没有buffer,所以是 Q 1 , Q 2 Q_1,Q_2 Q1,Q2完全对等的地位,用交替更新的方法打破对称性。在实际选择动作的时候用 Q 1 + Q 2 Q_1+Q_2 Q1+Q2

在交替更新的时候,都用需要更新的那个 Q Q Q 进行动作选择,然后另一个 Q ′ Q' Q′ 进行动作估计
(类似于 Deep Double Q-learning ,快 Q θ Q_{\theta} Qθ 用来选动作,慢 Q θ − Q_{\theta -} Qθ− 用来进行价值估计)


)







技术详解与实战)
)







(新版))