尺度函数与小波函数
尺度函数
设存在函数
φ j , k ( x ) = 2 j / 2 φ ( 2 j x − k ) \varphi_{j,k}(x)=2^{j/2}\varphi(2^{j}x-k) φj,k(x)=2j/2φ(2jx−k)
对所有的 j j j, k ∈ Z k{\in}\mathbb{Z} k∈Z 和 φ ( x ) ∈ L 2 ( R ) \varphi(x){\in}L^2(R) φ(x)∈L2(R)都成立。其中 k k k 决定了 φ j , k ( x ) \varphi_{j,k}(x) φj,k(x) 沿 x x x轴的位置, j j j 决定了 φ j , k ( x ) \varphi_{j,k}(x) φj,k(x) 的宽度,即它沿 x x x 轴宽或窄。项 2 j 2 ^{\frac{j}{{2}}} 2j控制函数的幅度。由于 φ j , k ( x ) \varphi_{j,k}(x) φj,k(x) 的形状随 j j j 发生变化,所以 φ ( x ) \varphi(x) φ(x)称为尺度函数。
设存在一个特定的值 j 0 j_0 j0,则可以得到集合 { φ j 0 , k ( x ) } \{\varphi_{j_0,k}(x)\} {φj0,k(x)}是集合 { φ j , k ( x ) } \{\varphi_{j,k}(x)\} {φj,k(x)}的一个子集。其中可以把由 φ j 0 , k ( x ) \varphi_{j_0,k}(x) φj0,k(x)张成的向量空间定义为 V j 0 V_{j_0} Vj0,即
V j 0 = S p a n { φ j 0 , k ( x ) } ‾ V_{j0}=\overline{{\mathop{\mathrm{Span}}\left\{\varphi_{j_0,k}(x)\right\}}} Vj0=Span{φj0,k(x)}
若 f ( x ) f(x) f(x)在 φ j 0 , k ( x ) \varphi_{j_0,k}(x) φj0,k(x)张成的空间中,则可以表示为
f ( x ) = ∑ k α k φ j 0 , k ( x ) f(x)=\sum_{k}\alpha_{k}\varphi_{j_0,k}(x) f(x)=k∑αkφj0,k(x)
更一般地,对于任何 j j j,我们将 k k k上跨越的子空间表示为
V j = S p a n { φ j , k ( x ) } ‾ V_{j}=\overline{{\mathrm{Span}\{\varphi_{j,k}(x)\}}} Vj=Span{φj,k(x)}
由于 j j j决定了 φ j , k ( x ) \varphi_{j,k}(x) φj,k(x)的宽或窄,即可以在x轴上表达更精细的特征,所以存在高分辨率的图像可以表示低分辨率的图像,即存在
V − ∞ ⊂ ⋯ ⊂ V − 1 ⊂ V 0 ⊂ V 1 ⊂ V 2 ⊂ ⋯ ⊂ V ∞ V_{-\infty}\subset\cdots\subset V_{-1}\subset V_{0}\subset V_{1}\subset V_{2}\subset\cdots\subset V_{\infty} V−∞⊂⋯⊂V−1⊂V0⊂V1⊂V2⊂⋯⊂V∞
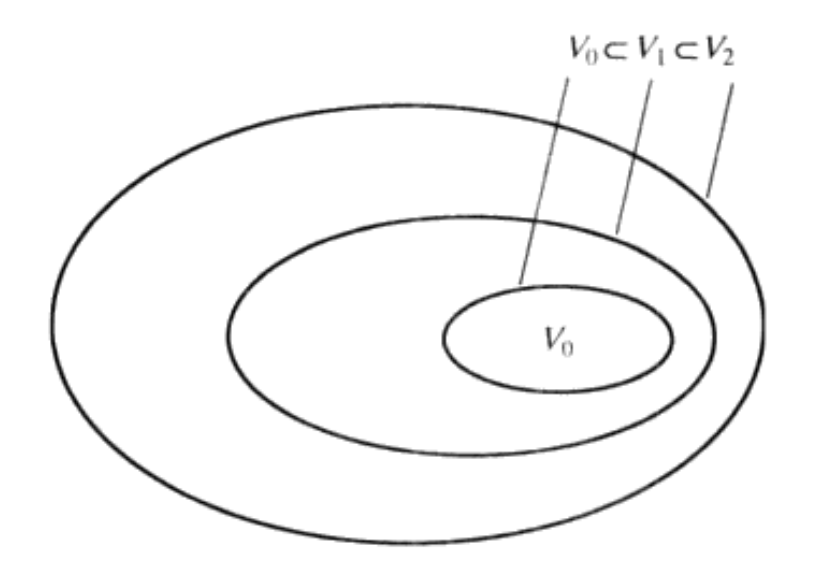
其中 V − ∞ = { 0 } , V ∞ = { L 2 ( R ) } V_{-\infty}=\left\{0\right\},V_{\infty}=\left\{L^{2}(R)\right\} V−∞={0},V∞={L2(R)}
因为 φ j , k ( x ) = 2 j / 2 φ ( 2 j x − k ) \varphi_{j,k}(x)=2^{j/2}\varphi(2^{j}x-k) φj,k(x)=2j/2φ(2jx−k),所以可得 φ j + 1 , k ( x ) = 2 ( j + 1 ) / 2 φ ( 2 j + 1 x − k ) \varphi_{j+1,k}(x)=2^{(j+1)/2}\varphi(2^{j+1}x-k) φj+1,k(x)=2(j+1)/2φ(2j+1x−k)
因为低分辨率的图像可以由高分辨率的图像所表示,所以存在
φ j , k ( x ) = ∑ n h φ ( n ) 2 ( j + 1 ) / 2 φ ( 2 j + 1 x − n ) \varphi_{j,k}(x)=\sum_{n}h_{\varphi}(n)2^{(j+1)/2}\varphi(2^{j+1}x-n) φj,k(x)=n∑hφ(n)2(j+1)/2φ(2j+1x−n)
若 j , k = 0 j,k=0 j,k=0,则可以写成
φ ( x ) = ∑ n h φ ( n ) 2 φ ( 2 x − n ) \varphi(x)=\sum_{n}h_{\varphi}(n)\sqrt{2}\varphi(2x-n) φ(x)=n∑hφ(n)2φ(2x−n)
该递归等式中的系数 h φ ( n ) h_{\varphi}(n) hφ(n)称为尺度函数系数; h φ h_{\varphi} hφ 为尺度向量。
其中简单尺度函数应符合多分辨率分析的四个条件
- **MRA要求1:**其中对于不同整数平移的简单尺度函数应是正交的
- **MRA要求2:**低尺度函数跨越的子空间应嵌入到高尺度跨越的子空间内
- **MRA要求3:**唯一对于所有 V j V_j Vj的通用的函数是 f ( x ) = 0 f(x)=0 f(x)=0
- **MRA要求4:**任何函数都可以任意精度表示
小波函数
定义小波函数 ψ ( x ) \psi\left(x\right) ψ(x)为 V j + 1 V_{j+1} Vj+1与 V j V_j Vj之差,其中
ψ j , k ( x ) = 2 j / 2 ψ ( 2 j x − k ) \psi_{j,k}(x)=2^{j/2}\psi(2^{j}x-k) ψj,k(x)=2j/2ψ(2jx−k)
其中尺度函数与小波函数的关系如下图所示
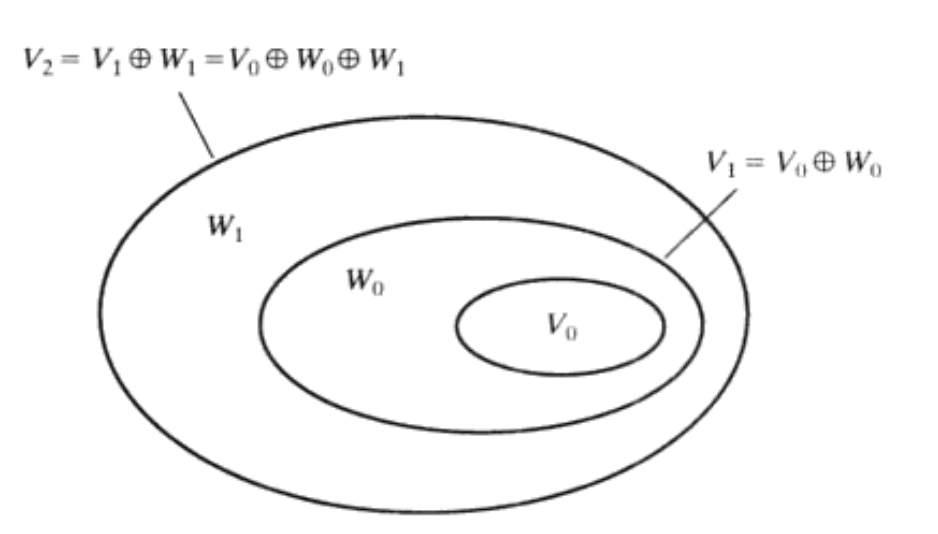
其中 W j = S p a n { ψ j , k ( x ) } ‾ W_{j}=\overline{{\mathrm{Span}\{\psi_{j,k}(x)\}}} Wj=Span{ψj,k(x)},所以存在 V j + 1 = V j ⊕ W j V_{j+1}=V_{j}\oplus W_{j} Vj+1=Vj⊕Wj
其中, ⊕ \oplus ⊕ 表示空间的并集(类似于集合的并集)。 V j + 1 V_{j+1} Vj+1 中 V j V_j Vj的正交补集是 W j W_j Wj, 且 V j V_j Vj中的所有成员对于 W j W_j Wj中的所有成员都正交。因此,
⟨ φ j , k ( x ) , ψ j , l ( x ) ⟩ = 0 \left\langle\varphi_{j,k}(x),\psi_{j,l}(x)\right\rangle=0 ⟨φj,k(x),ψj,l(x)⟩=0
对所有适当的 j , k , l ∈ Z j,k,l\in\mathbb{Z} j,k,l∈Z都成立。
索引可以将所有可度量的、平方可积的函数空间表示为
L 2 ( R ) = V 0 ⊕ W 0 ⊕ W 1 ⊕ ⋯ L^{2}(R)=V_{0}\oplus W_{0}\oplus W_{1}\oplus\cdots L2(R)=V0⊕W0⊕W1⊕⋯
L 2 ( R ) = V 1 ⊕ W 1 ⊕ W 2 ⊕ ⋯ L^{2}(\boldsymbol{R})=V_{1}\oplus W_{1}\oplus W_{2}\oplus\cdots L2(R)=V1⊕W1⊕W2⊕⋯
L 2 ( R ) = ⋯ ⊕ W − 2 ⊕ W − 1 ⊕ W 0 ⊕ W 1 ⊕ W 2 ⊕ ⋯ L^{2}(\boldsymbol{R})=\cdots\oplus W_{-2}\oplus W_{-1}\oplus W_{0}\oplus W_{1}\oplus W_{2}\oplus\cdots L2(R)=⋯⊕W−2⊕W−1⊕W0⊕W1⊕W2⊕⋯
上述表达排除了尺度函数,仅采用小波进行表示
于是存在
L 2 ( R ) = V j 0 ⊕ W j 0 ⊕ W j 0 + 1 ⊕ ⋯ L^{2}(\boldsymbol{R})=V_{j_{0}}\oplus W_{j_{0}}\oplus W_{j_{0}+1}\oplus\cdots L2(R)=Vj0⊕Wj0⊕Wj0+1⊕⋯
其中 j 0 j_{0} j0是任意开始尺度。
因为小波空间位于相邻的较高分辨率的尺度空间中,即 W i ⊂ V i + 1 W_i\sub V_{i+1} Wi⊂Vi+1,所以任何小波函数可以使用尺度函数表示,即
ψ ( x ) = ∑ n h ψ ( n ) 2 φ ( 2 x − n ) \psi(x)=\sum_{n}h_{\psi}(n)\sqrt{2}\varphi(2x-n) ψ(x)=n∑hψ(n)2φ(2x−n)
其中 h ψ ( n ) h_{\psi}(n) hψ(n)被称为小波函数系数
因为整数小波彼此正交,且与他们的互补尺度函数正交,所以存在
h ψ ( k ) = ( − 1 ) k h φ ( 1 − k ) h_{\psi}(k)=\left(-1\right)^{k}h_{\varphi}(1-k) hψ(k)=(−1)khφ(1−k)



)





 格林威治时间)




是一个字符串替换的函数,用于将指定的字符串或模式在目标字符串中进行替换)




)