一、介绍
在不断发展的机器学习领域,算法的效率至关重要。大 O 表示法成为这方面的一个关键工具,它提供了一种描述算法性能或复杂性的语言,特别是在时间和空间方面。本文探讨了 Big O 表示法在机器学习中的重要性,阐明了它在算法选择、优化和整体系统设计中的作用。
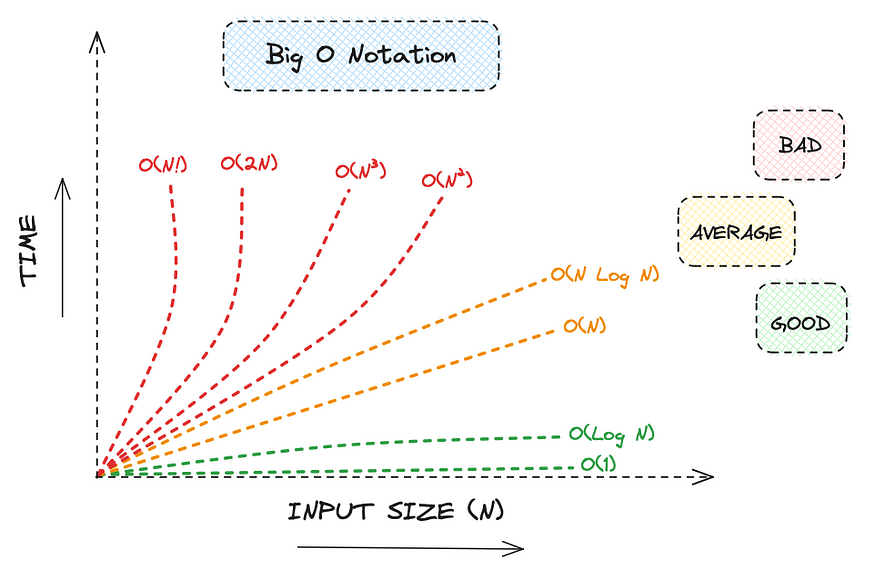
在机器学习领域,理解 Big O 表示法不仅仅是衡量复杂性;还包括测量复杂性。它是关于释放效率、可扩展性以及将数据转化为智慧的潜力。
二、理解大 O 表示法
大 O 符号根据函数的增长率来表征函数。它在算法分析中至关重要,可以提供对算法在输入大小方面的行为的高级理解。常见的 Big O 表示法包括常数时间的 O(1)、线性时间的 O(n)、对数时间的 O(log n) 以及更复杂的形式,例如二次时间的 O(n²) 和二次时间的 O(2^n)指数时间。
三、Big O 在机器学习中的作用
算法选择
在机器学习中,选择正确的算法对于有效的模型训练和预测至关重要。大 O 表示法通过提供对算法的时间和空间复杂性的洞察来帮助这个选择过程。例如,复杂度为 O(n²) 的算法对于小型数据集可能是可行的,但对于较大的数据集就变得不切实际。了解这些复杂性有助于为给定的数据大小和问题类型选择最有效的算法。
模型优化
机器学习涉及处理大型数据集和复杂模型。这些模型的优化对于提高性能和降低计算成本至关重要。 Big O 表示法有助于识别算法中的瓶颈,指导开发人员更有效地实现。例如,将复杂度从 O(n²) 降低到 O(n log n) 可以显着加快模型的训练时间。
可扩展性和实际应用
机器学习模型的可扩展性是一个至关重要的问题,特别是对于数据量巨大的现实场景中的应用程序。 Big O 表示法提供了一个评估和确保算法可扩展性的框架。复杂度较低的算法更具可扩展性,更适合大规模应用,例如实时数据分析和高频交易系统。
时间与空间的权衡
大 O 表示法还阐明了算法设计中的时空权衡。有些算法可能很快(时间复杂度较低)但消耗更多内存(空间复杂度较高),反之亦然。了解这种权衡对于机器学习至关重要,因为时间和内存资源都可能是限制因素。
挑战和考虑因素
虽然大 O 表示法是一个强大的工具,但它并非没有局限性。它提供渐近分析,可能并不总是准确反映现实世界的性能。此外,它没有考虑硬件效率、并行计算能力和数据结构选择等因素,这些因素会显着影响机器学习算法的实际性能。
四、代码
创建一个完整的 Python 示例来演示 Big O 表示法在机器学习中的应用涉及几个步骤。我们将:
- 生成合成数据集。
- 实施具有不同复杂性的机器学习算法。
- 测量并绘制这些算法相对于数据集大小的性能,以说明它们的 Big O 复杂性。
第 1 步:生成综合数据集
我们将使用sklearn.datasets.make_regression 创建回归问题的综合数据集。该函数允许我们控制样本数量,这对于分析算法在不同数据集大小下的性能至关重要。
第 2 步:实施机器学习算法
我们将重点关注两种算法:
- 线性回归 (O(n)):复杂度通常为线性或接近线性。
- K 最近邻 (KNN) (O(n²)):暴力实现的复杂度通常是二次方。
第 3 步:测量并绘制性能图
我们将测量在不同大小的数据集上训练这些模型所需的时间,并绘制这些时间以可视化 Big O 复杂性。
我们来写一下代码:
import numpy as np
import matplotlib.pyplot as plt
import time
from sklearn.linear_model import LinearRegression
from sklearn.neighbors import KNeighborsRegressor
from sklearn.datasets import make_regression# Initialize the range of dataset sizes and an empty list to store performance metrics
dataset_sizes = np.linspace(100, 1000, 10, dtype=int)
linear_regression_times = []
knn_times = []for size in dataset_sizes:# Generate a synthetic datasetX, y = make_regression(n_samples=size, n_features=5, noise=0.1)# Measure performance for Linear Regressionstart_time = time.time()linear_model = LinearRegression().fit(X, y)linear_regression_times.append(time.time() - start_time)# Measure performance for K-Nearest Neighborsstart_time = time.time()knn_model = KNeighborsRegressor().fit(X, y)knn_times.append(time.time() - start_time)# Plotting the results
plt.figure(figsize=(10, 6))
plt.plot(dataset_sizes, linear_regression_times, label='Linear Regression (O(n))')
plt.plot(dataset_sizes, knn_times, label='KNN (O(n^2))')
plt.xlabel('Dataset Size')
plt.ylabel('Training Time (seconds)')
plt.title('Algorithm Complexity Analysis using Big O Notation')
plt.legend()
plt.show()
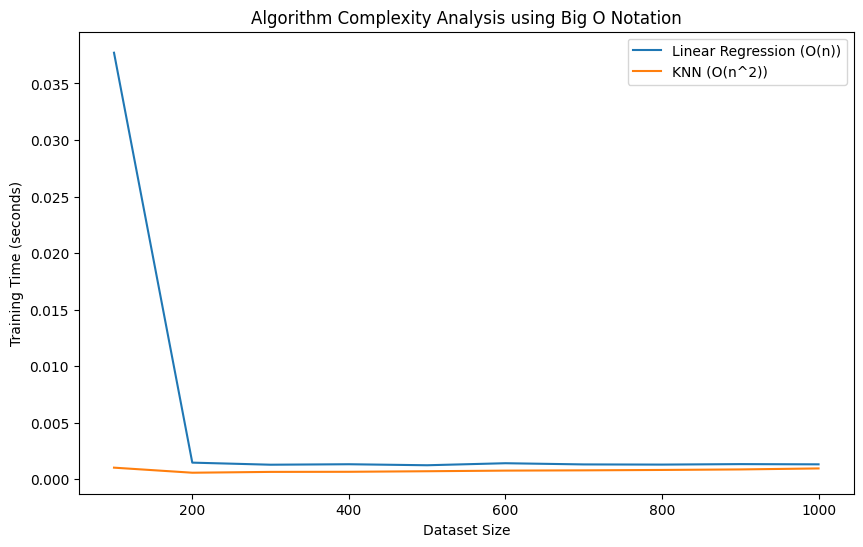
该脚本将生成一个图,显示每个算法的训练时间如何随数据集的大小变化。线性回归线应显示训练时间随数据集大小呈近线性增加,反映其 O(n) 复杂度。相比之下,KNN 线应该显示出训练时间的更快增加,反映出其更高的复杂性,对于暴力实现来说通常是 O(n²)。
五、结论
大O表示法在机器学习领域发挥着基础作用。它有助于算法的选择、优化和可扩展性评估。虽然它是一个抽象概念,可能无法捕获算法性能的所有方面,但它在指导开发人员获得高效且有效的机器学习解决方案方面的重要性怎么强调也不为过。随着机器学习的不断发展和发展,大 O 表示法在驾驭这一复杂领域的相关性仍然没有减弱。





 ——模版语法1)

PostgreSQL下载与安装)








)


)