算法训练营Day14

#Java #二叉树层次遍历 #反转二叉树

开源学习资料

二叉树的层次遍历：力扣题目链接

二叉树的层次遍历很好理解：

就是从根结点一层一层地往下遍历（同一层，从左到右）：

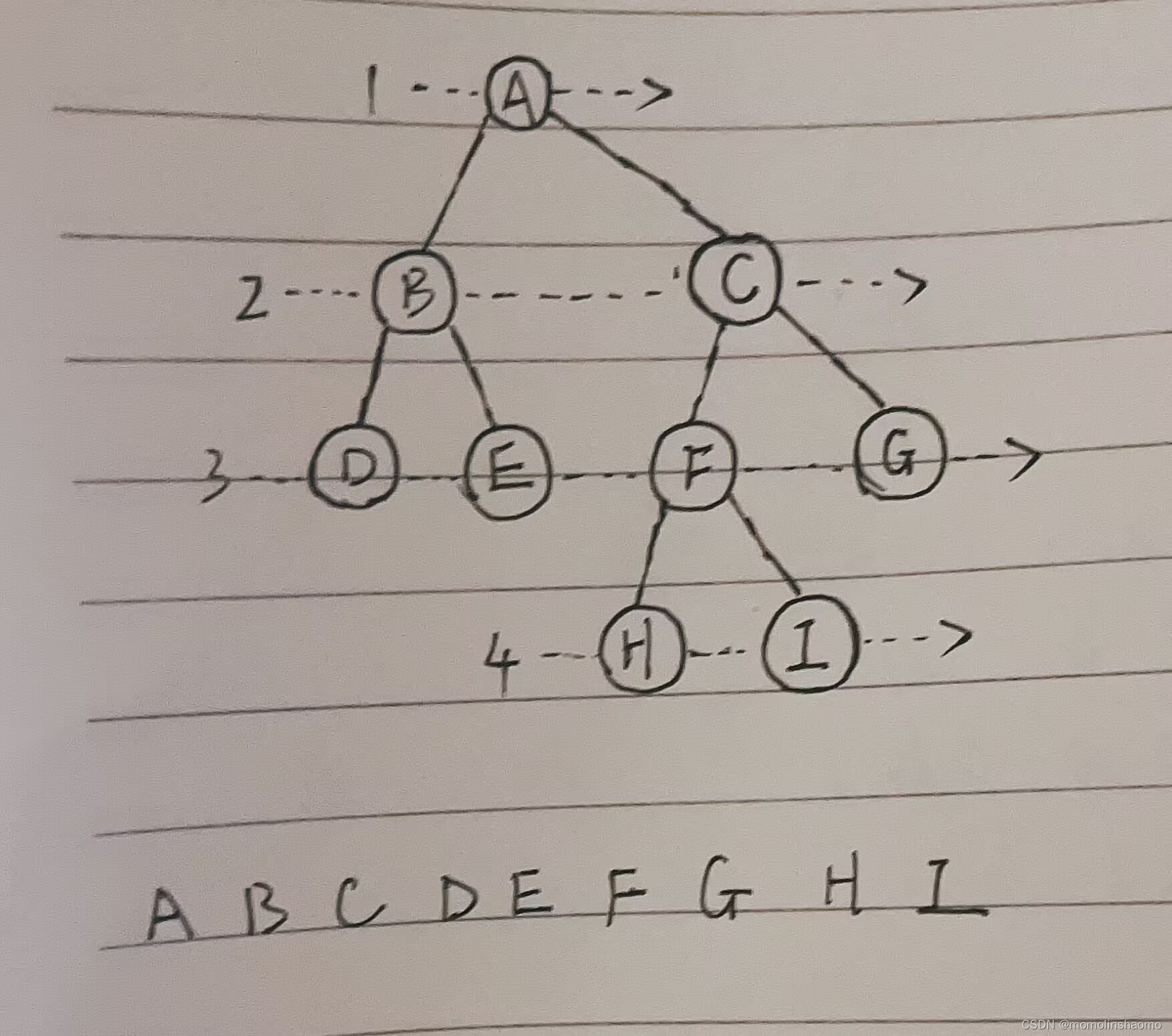
迭代的方式很好理解：就是依次入队出队。

但是判断条件怎么写？

最需要解决的就是，要把节点依次入队，那要怎么记录这些节点，防止它们丢失。

第一步把根节点先入队，这时候要想让它的左孩子和右孩子入队（如上图），就要在A出队的时候，记录它。

关键的就是在一个节点出队的时候，记录该节点，就能找到它的左右孩子。

/*** Definition for a binary tree node.* public class TreeNode {*     int val;*     TreeNode left;*     TreeNode right;*     TreeNode() {}*     TreeNode(int val) { this.val = val; }*     TreeNode(int val, TreeNode left, TreeNode right) {*         this.val = val;*         this.left = left;*         this.right = right;*     }* }*/
class Solution {public List<List<Integer>> res = new ArrayList<>();public List<List<Integer>> levelOrder(TreeNode root) {if(root == null){return res;}//模拟成一个队列//从根节点开始，依次入队（从左到右）Queue<TreeNode> queue = new LinkedList<>(); //创建一个队列//根节点先入队queue.offer(root);while(!queue.isEmpty()){int len = queue.size();List<Integer> list  = new ArrayList<>();while(len>0){//记录出队的节点TreeNode node = queue.poll();list.add(node.val);if(node.left!=null){//左孩子入队queue.offer(node.left);}if(node.right!=null){//右孩子入队queue.offer(node.right);}len--;}res.add(list);}return res;}
}

用两个while循环，主要是为了满足结果形式，保证每个结果都保存在一个新的集合中。

不然就是这样的（结果不能反映出是层次遍历）：

先使用DFS迭代遍历练习以下题目：

二叉树的层序遍历II：力扣题目链接

给你二叉树的根节点 root ，返回其节点值 自底向上的层序遍历 。（即按从叶子节点所在层到根节点所在的层，逐层从左向右遍历）

/*** Definition for a binary tree node.* public class TreeNode {*     int val;*     TreeNode left;*     TreeNode right;*     TreeNode() {}*     TreeNode(int val) { this.val = val; }*     TreeNode(int val, TreeNode left, TreeNode right) {*         this.val = val;*         this.left = left;*         this.right = right;*     }* }*/class Solution {List<List<Integer>> res = new LinkedList<>();public List<List<Integer>> levelOrderBottom(TreeNode root) {Queue<TreeNode> que = new LinkedList<>();if(root == null){return res;}//先把根节点入队que.offer(root);while(!que.isEmpty()){List<Integer> list = new ArrayList<>();int size = que.size();//每一层入队出队for(int i =0;i<size;i++){TreeNode node = que.poll();list.add(node.val);if(node.left != null){que.offer(node.left);}if(node.right != null){que.offer(node.right);}}res.add(0,list);}return res;}
}

思路相同，只是用了链表的翻转。

二叉树的右视图：力扣题目链接

给定一个二叉树的 根节点 root，想象自己站在它的右侧，按照从顶部到底部的顺序，返回从右侧所能看到的节点值。

/*** Definition for a binary tree node.* public class TreeNode {*     int val;*     TreeNode left;*     TreeNode right;*     TreeNode() {}*     TreeNode(int val) { this.val = val; }*     TreeNode(int val, TreeNode left, TreeNode right) {*         this.val = val;*         this.left = left;*         this.right = right;*     }* }*/
class Solution {public List<Integer> rightSideView(TreeNode root) {List<Integer> list = new ArrayList<>();Deque<TreeNode> que = new LinkedList<>();if (root == null) {return list;}que.offer(root);while (!que.isEmpty()) {int levelSize = que.size();for (int i = 0; i < levelSize; i++) {TreeNode node = que.poll();if (node.left != null) {que.offer(node.left);}if (node.right != null) {que.offer(node.right);}//就多一步：//只要最右边的：if (i == levelSize - 1) {list.add(node.val);}}}return list;}
}

这道题就关键的一步：只把最右边的放到结果中！

二叉树的层平均值：力扣题目链接

给定一个非空二叉树的根节点 root , 以数组的形式返回每一层节点的平均值。

/*** Definition for a binary tree node.* public class TreeNode {*     int val;*     TreeNode left;*     TreeNode right;*     TreeNode() {}*     TreeNode(int val) { this.val = val; }*     TreeNode(int val, TreeNode left, TreeNode right) {*         this.val = val;*         this.left = left;*         this.right = right;*     }* }*/
class Solution {public List<Double> averageOfLevels(TreeNode root) {List<Double> list = new ArrayList<>();Queue<TreeNode> que = new LinkedList<>();if(root==null){return list;}que.offer(root);while(!que.isEmpty()){int size = que.size();Double sum =0.0;for(int i =0 ;i<size;i++){TreeNode node = que.poll();sum+=node.val;if(node.left!=null){que.offer(node.left);}if(node.right!=null){que.offer(node.right);}}Double average = sum/size;list.add(average);}return list;}
}

一层一层计算！

N叉树的层序遍历：力扣题目链接

给定一个 N 叉树，返回其节点值的层序遍历。 (即从左到右，逐层遍历)。

/*
// Definition for a Node.
class Node {public int val;public List<Node> children;public Node() {}public Node(int _val) {val = _val;}public Node(int _val, List<Node> _children) {val = _val;children = _children;}
};
*/class Solution {public List<List<Integer>> levelOrder(Node root) {if (root == null) {return new ArrayList<List<Integer>>();}List<List<Integer>> ans = new ArrayList<List<Integer>>();Queue<Node> queue = new ArrayDeque<Node>();queue.offer(root);while (!queue.isEmpty()) {int cnt = queue.size();List<Integer> level = new ArrayList<Integer>();for (int i = 0; i < cnt; ++i) {Node cur = queue.poll();level.add(cur.val);for (Node child : cur.children) {queue.offer(child);}}ans.add(level);}return ans;}
}

在每个树行中找最大值：力扣题目链接

您需要在二叉树的每一行中找到最大的值。

/*** Definition for a binary tree node.* public class TreeNode {*     int val;*     TreeNode left;*     TreeNode right;*     TreeNode() {}*     TreeNode(int val) { this.val = val; }*     TreeNode(int val, TreeNode left, TreeNode right) {*         this.val = val;*         this.left = left;*         this.right = right;*     }* }*/
class Solution {public List<Integer> largestValues(TreeNode root) {if(root == null){return Collections.emptyList();}List<Integer> result = new ArrayList();Queue<TreeNode> queue = new LinkedList();queue.offer(root);while(!queue.isEmpty()){int max = Integer.MIN_VALUE;for(int i = queue.size(); i > 0; i--){TreeNode node = queue.poll();max = Math.max(max, node.val);if(node.left != null) queue.offer(node.left);if(node.right != null) queue.offer(node.right);}result.add(max);}return result;}
}

二叉树的最大深度：力扣题目链接

给定一个二叉树 root ，返回其最大深度。

二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。

class Solution {public int maxDepth(TreeNode root) {if (root == null)   return 0;//先创建一个队列Queue<TreeNode> que = new LinkedList<>();//利用层次遍历//加入节点que.offer(root);int deep =0;while(!que.isEmpty()){int len = que.size();while(len>0){TreeNode node = que.poll();if(node.left!=null) que.offer(node.left);if(node.right!=null) que.offer(node.right);len--;}deep++;}return deep;}
}

二叉树的最小深度：力扣题目链接

给定一个二叉树，找出其最小深度。

最小深度是从根节点到最近叶子节点的最短路径上的节点数量。

/*** Definition for a binary tree node.* public class TreeNode {*     int val;*     TreeNode left;*     TreeNode right;*     TreeNode() {}*     TreeNode(int val) { this.val = val; }*     TreeNode(int val, TreeNode left, TreeNode right) {*         this.val = val;*         this.left = left;*         this.right = right;*     }* }*/
class Solution {public int minDepth(TreeNode root) {Queue<TreeNode> que = new LinkedList<>();if(root == null){return 0;}que.offer(root);int deep=0;while(!que.isEmpty()){int size = que.size();deep++;for(int i =0;i<size;i++){TreeNode node = que.poll();if(node.left==null && node.right==null){return deep;}if(node.left!=null){que.offer(node.left);}if(node.right!=null){que.offer(node.right);}}}return deep;}
}

利用层序遍历快速刷完了这几道题，发现基本都是一个模板，只是根据每一个题的要求作出一些改变，大体上还是一模一样的。

体会：在外层while中执行的就是当前位置要做的事情，而内层的for循环/while循环，就为下一层做好准备，而size则是控制每层中的节点。

翻转二叉树：力扣题目链接

翻转一棵二叉树。

力扣示例：

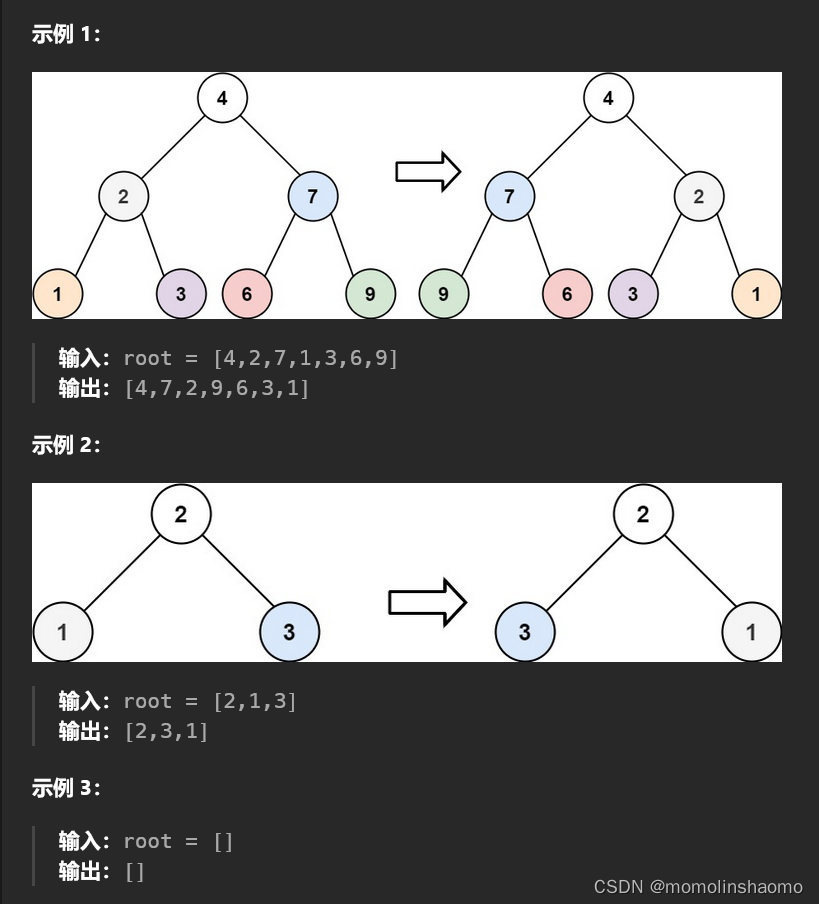
这道题用递归来写：

/*** Definition for a binary tree node.* public class TreeNode {*     int val;*     TreeNode left;*     TreeNode right;*     TreeNode() {}*     TreeNode(int val) { this.val = val; }*     TreeNode(int val, TreeNode left, TreeNode right) {*         this.val = val;*         this.left = left;*         this.right = right;*     }* }*/
class Solution {public TreeNode invertTree(TreeNode root) {//利用递归//递归出口：if(root == null){return null;}invertTree(root.left);invertTree(root.right);swap(root);return root;}//交换的方法public void swap(TreeNode root){TreeNode temp = root.left;root.left = root.right;root.right = temp;}
}

代码很简单，但是要深刻理解递归！

1.递归的出口

2.方法的返回值

当 root 为 null 时，递归的出口就是返回 null。这是因为在二叉树的递归操作中，每个递归步骤都涉及到对左右子树的处理，而 null 表示一个空节点或者叶子节点的空子树。

在这个具体的情境中，当 invertTree 方法递归到叶子节点的左右子树时，这些子树是空的，因此将它们反转后仍然为空。返回 null 可以告诉上一级递归调用，这个空节点的左右子树已经反转完成。

return root，是为了在递归结束后返回整个树反转后的根节点。

再来练习一道：

对称二叉树:力扣题目链接

给定一个二叉树，检查它是否是镜像对称的。

/*** Definition for a binary tree node.* public class TreeNode {*     int val;*     TreeNode left;*     TreeNode right;*     TreeNode() {}*     TreeNode(int val) { this.val = val; }*     TreeNode(int val, TreeNode left, TreeNode right) {*         this.val = val;*         this.left = left;*         this.right = right;*     }* }*/
class Solution {public boolean isSymmetric(TreeNode root) {if(root == null){return true;}return dfs(root.left,root.right);}boolean dfs(TreeNode left , TreeNode right){//递归结束条件：//左右子树都为空if(left == null && right ==null){return true;}//左右节点有一个为空if(left == null || right == null){return false;}//左右节点的值不相等if(left.val != right.val){return false;}return dfs(left.left,right.right) && dfs(left.right,right.left);}
}

这些都是比较简单的递归，思想主要是抓住：

方法的返回值

递归的终止条件

确定递归的单层逻辑

在代码随想录中有对这三部曲的详细概括！即时Review~~~~

我自光芒万丈，

何须他人半点光！

Fighting！