C++——红黑树

作者：几冬雪来

时间：2023年12月7日

内容：C++——红黑树讲解

前言：

红黑树的概念：

红黑树的性质：

红黑树的路径计算：

最长路径和最短路径：

AVL树与红黑树的区别：

红黑树的框架：

红黑树插入节点：

插入节点颜色的变化：

颜色变化的特殊情况：

变色与旋转：

判断是否为红黑树：

代码：

结尾：

前言：

在上一篇博客中我们讲解了在C++两棵重要的树中的一棵树，也就是AVL树。而另一棵树就是今天要对其讲解的红黑树。而红黑树也算C++板块的一个重要的知识点，在解题的时候经常被使用。

红黑树的概念：

在上一篇博客讲解AVL树的时候就有谈到过，红黑树和AVL树都属于二叉搜索树的一个延伸，二者的做法差不多，但是其性质却不一样。

这里的红黑树，顾名思义就是在每个结点上都增加一个储存为表示该节点的颜色，可以说红或者黑色。而对比起之前讲解的C++的AVL树，红黑树会在一定程度上更优一点。

红黑树在一定程度上占优，这是因为AVL树过于严格了，它必须保证最高的结点减去最短结点后高度要小于2或者大于-2。

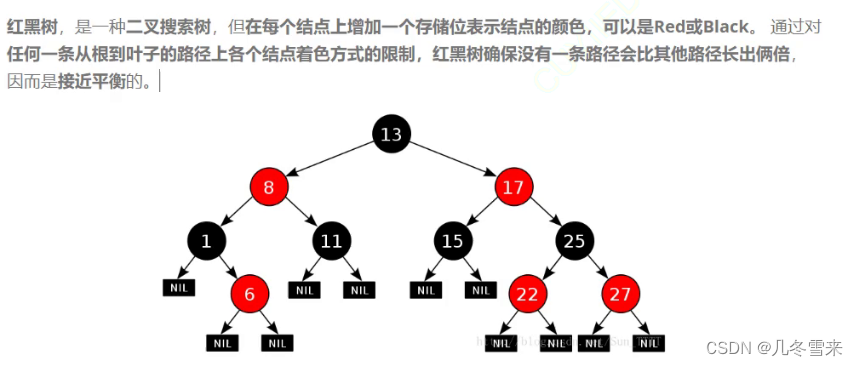
这个地方红黑树的做法是，使得每个结点都有红黑两种颜色限制达到最长路径不超过最短路径的两倍。

但是这种行为也有它的弊端，那就是对比AVL树，AVL树的平衡是几乎平衡而红黑树的平衡只是近似平衡而且，且在插入相同数量结点的情况下红黑树的高度要较高于AVL树。

虽然红黑树的高度相较于AVL树要高，但是其效率却不输AVL树。

红黑树的性质：

在讲解完了红黑树的概念之后，接下来就来说一说红黑树的性质。

这里看一下红黑树的4个性质，第一个要求每个结点不是黑的就是红色的。

接下来就是规定了根节点必须是黑色的。

第三条性质讲解了，在红黑树中的任何路径没有连续的两个同为红色的结点。

这个地方的最后一条说明了，每条路径都包含了相同数量的黑色结点。

红黑树的路径计算：

在上面最后一条性质讲了，红黑树的每条路径都包含了相同数量的黑色结点。

那么这个地方就延伸出一个问题，红黑树要怎么去数它路径的多少，就以刚刚上边的那张红黑树的图为例：

这里路径数量的计算方式是，从根节点到空节点算一条路径，因此要算该红黑树有多少路径的话，最优的方法就是看它空节点的数量是多少。

最长路径和最短路径：

在了解完了红黑树路径的计算后，接下来我们就来看看它的最长和最短路径是如何得出的。在AVL树中我们可以得知，最长路径和最短路径是相互限制的，最长路径不能超过最短路径的高度差不超过1。

而在红黑树中最长路径和最短路径有了新的变化。

首先红黑树的最短路径如上图的左子树，全为黑色结点的路径就为最短路径。而最长路径则是一红一黑相间的路径。

AVL树与红黑树的区别：

在初步了解完了红黑树之后，接下来就是要让红黑树与先前学习的AVL树做对比，对比二者的优缺点。

首先就是二者的时间复杂度。

从图中可以看出红黑树的时间复杂度是AVL树的两倍，但是先前我们又讲解过红黑树要优于AVL树，这是因为二者处于同一量级，对此一倍与两倍对编译器的效率影响可以忽略不计。

话虽如此，但是AVL树看起来时间复杂度是比AVL树小的，同时前面也有说明AVL树是被严格控制平衡的，红黑树只是近似平衡。

但是AVL树严格控制平衡会有一定的代价，那就是AVL树在插入和删除的时候需要进行大量的旋转操作，而红黑树对比AVL树不需要大量的旋转操作。

红黑树的框架：

和书写AVL一样，书写红黑树也要有一个它自己的框架，又因为红黑树不用动用到平衡因子，因此也就不需要一个整形来存放平衡因子的值，二者框架的代码也会略微不同。

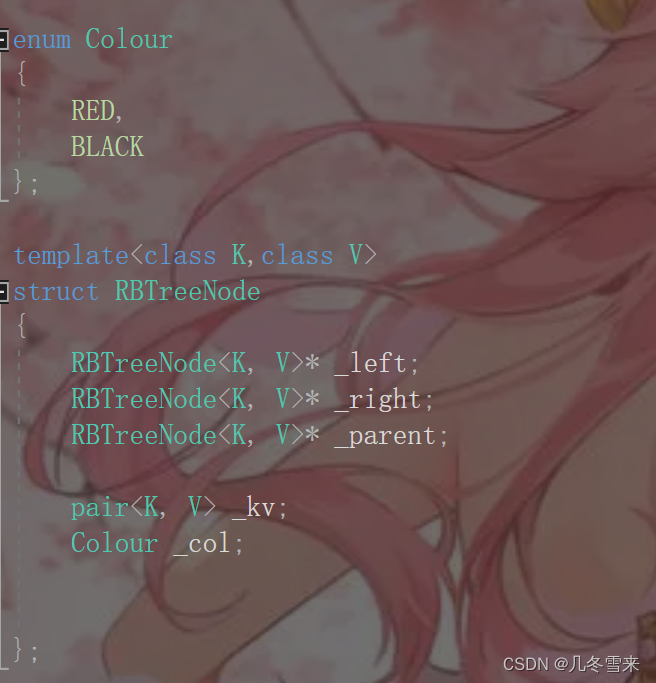
在这个地方依旧的要创建一个左结点，一个右结点和一个父结点。而后再借用map的pair创建一个_kv。

与AVL在这个地方创建一个整形类型的_bf来储存平衡因子不同，红黑树因为没有平衡因子所以不需要创建_bf来使用。

但是红黑树在这里涉及到了结点的颜色，因此此处要用一个枚举函数枚举出RED和BLACK两种颜色。

再然后对它们进行初始化，这里的col就从RED与BLACK中随机选一个颜色进行初始化即可。、

红黑树插入节点：

在书写完了框架之后，接下来就是红黑树节点的插入。

因为红黑树和AVL树都是二叉搜索树的延伸，因此在书写插入代码的时候二者十分的相似，这里我们就可以使用CV操作，将AVL树插入的代码拷贝过来。

但是在红黑树的性质那里有规定，根节点的颜色必须为黑色，因此当根节点为空第一次插入结点的时候，这里要将这个节点的颜色设计为黑色。

而在插入首个节点，接下来每个新插入节点的颜色会带来一些问题，也就是我们它的节点颜色是红色还是黑色。

要解决这个问题，这里需要返回到之前红黑树性质的4条规则那里。

在这里着重要关注的是第3条与第4条规则。

如果插入的结点颜色为黑色的话，这个地方可能会使得第四条规则违规，因为规则里面有说要保证每个路径的黑色节点的个数相同，要是增加的节点颜色为黑色的话，最终会导致该路径的黑节点的个数与其他路径的不一致。

如果新插入节点为红色，那这个地方要保证期父节点的颜色不为红色。

因此插入的新节点颜色只能为红色，并且要对新节点的父节点进行判断。

插入节点颜色的变化：

在上文我们讲解到红黑树插入的新节点的颜色必然是红色，而且如果插入的新节点的父节点也会红色的话，这里就要进行节点变色的操作。

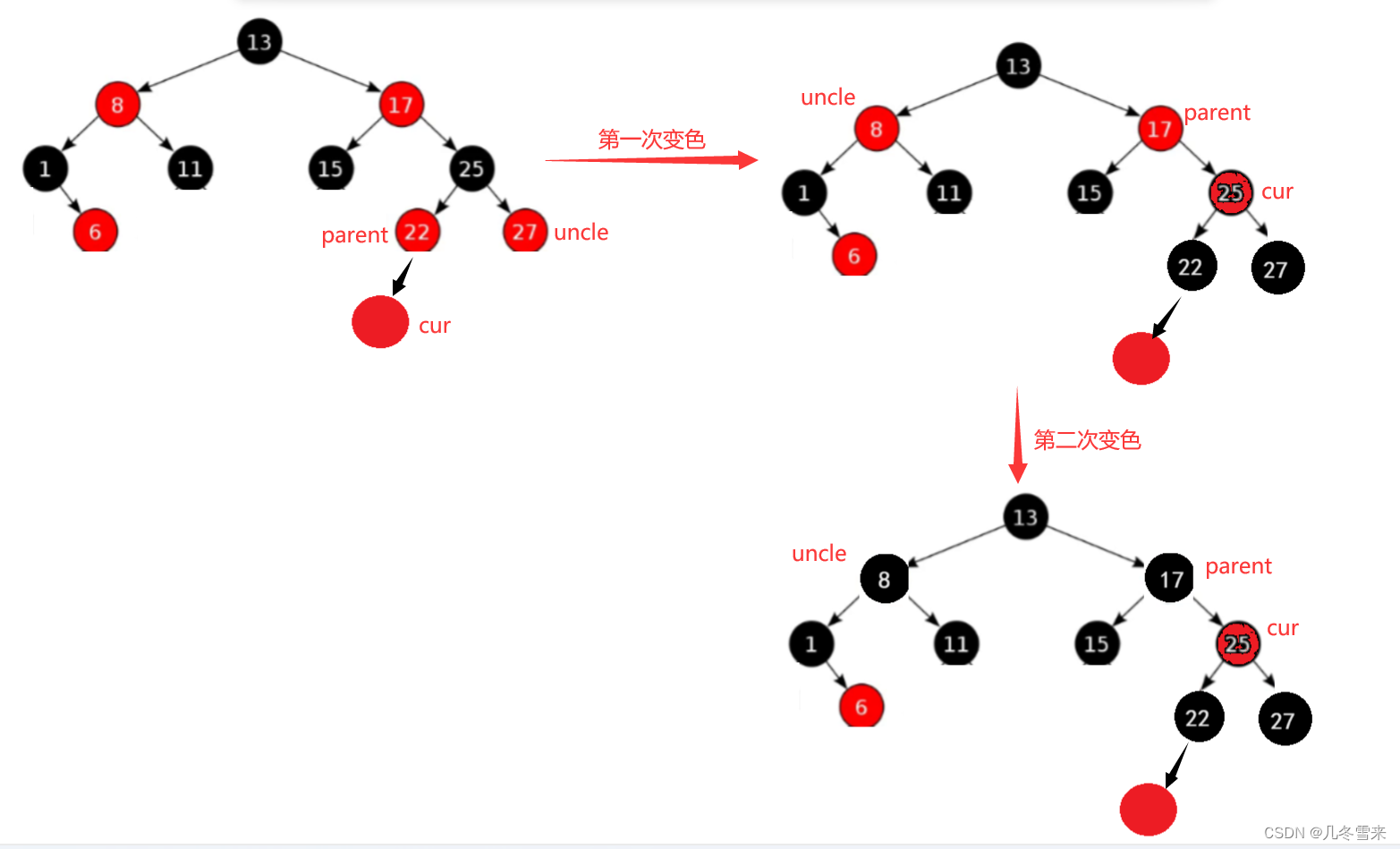
首先就是将新插入的节点定义为cur，接下来将它父节点定义为parent同时将parent的父节点的另一边节点定义为uncle。

如果新插入的节点cur与parent的颜色同为红色的话，这里就违反了规则不能有两个红色的节点连续。

因此parent结点就需要更改为黑色，又因为在红黑树中每条路径黑色结点的数量必须都一样，所以uncle要换为黑色，同时也因为每条路径黑色节点的数量不能改变，所以uncle的父节点要换为红色，如果parent的父节点为红且不为根节点的话，我们就继续向上处理。

因此这个地方就总结出来了几个情况：

1.如果grandfather没有父亲，也就是grandfather为根，只需要将其变黑即可

2.如果grandfather有父亲，且它的父亲为黑色，则结束运行

3. 如果grandfather有父亲，它的颜色为红色，这里就要向上处理，cur为第一次修改的grandfather位置

颜色变化的特殊情况：

在什么我们得知了插入节点后节点颜色变化的规律，插入的必然是红节点，如果其父节点与uncle也为红节点的话，就要将它与uncle节点都改为黑色。

接下来再判断它们的grandfather的颜色与有无父节点来决定要不要继续向上处理。

但是这里可能会出现一些特殊的情况。

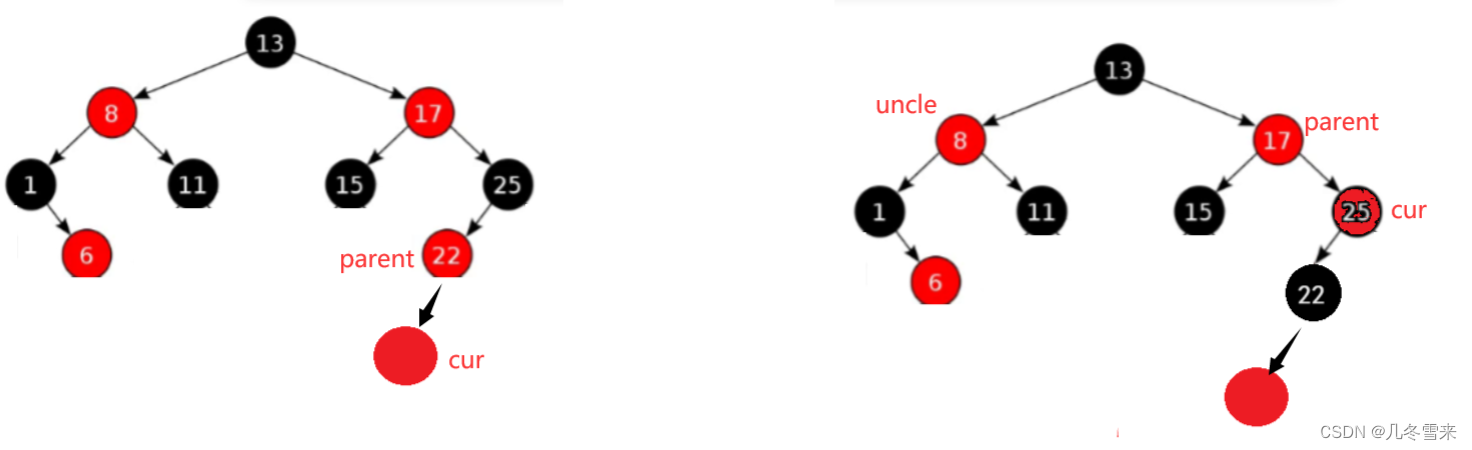
就如同上图，新添加的cur节点它的父节点为红色，但是这里并没有uncle节点。

这样就意味着，这个地方我们不能直接去修改parent与grandfather的颜色，如果修改后就会和上图一样，有一条路径的黑色节点的个数变少了。

这个地方的另一种特殊情况则是增加节点导致了最长路径超过了最短路径的两倍，在这种情况下我们也不能只是单纯的对其进行换色操作。

而且这里为了解决这些问题就要利用到AVL树中的旋转操作了，同时这里的旋转也是有单旋和双旋的做法。

就拿最长路径超过了最短路径的两倍的特殊情况来举例，这个地方要使这棵错误的红黑树变为正常的红黑树。

首先就是以值为25的结点为旋转点进行一次右旋的操作，使得最长路径与最短路径在两倍或者两倍以内，再旋转后才能判断后对节点进行上色操作。

同样的红黑树没有uncle节点也是通过旋转再上色的操作完成的。

因此这里我们就得出了一些特殊情况：

1.uncle节点不存在的情况

2.uncle节点存在，且该节点颜色为黑

3.uncle节点存在，且该节点颜色为红

同时也对上面特殊情况的处理做了总结：

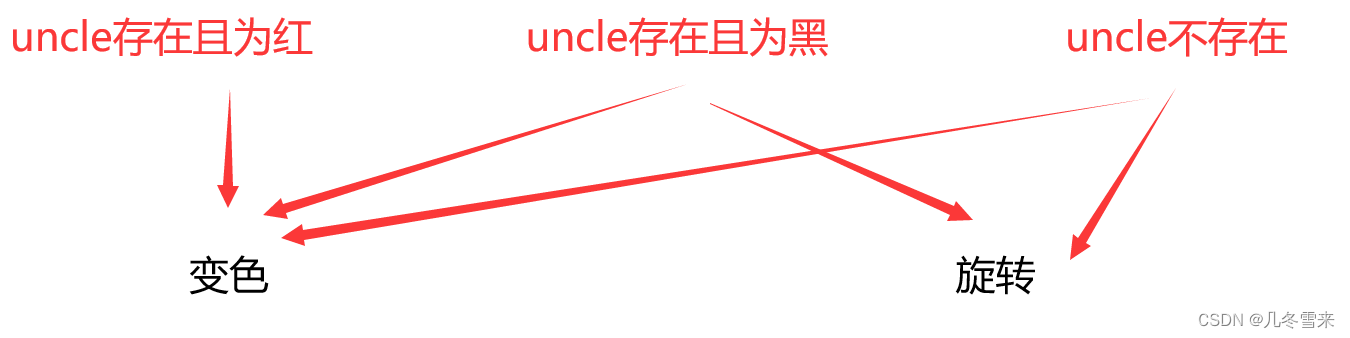
1.如果uncle存在且为红，则进行变色操作后再向上处理

2.如果uncle不存在或者存在且为黑，则先进行旋转操作后再进行换色操作

这里我们也能看出红黑树插入后的旋转或者变色操作，关键还是要看uncle。

变色与旋转：

在进行完了节点插入的操作，并且也清楚的了解了红黑树的节点颜色的一些规矩，并且也知道了红黑树的变色与旋转操作，关键是在于uncle节点的情况。

但是使得上下两个连接的节点都呈现红色的情况不单单只有parent为红节点，cur为新插入的节点这一种操作而已。

下来我们就来讲解在哪些情况会出现下上下两个连接节点都为红色的情况。

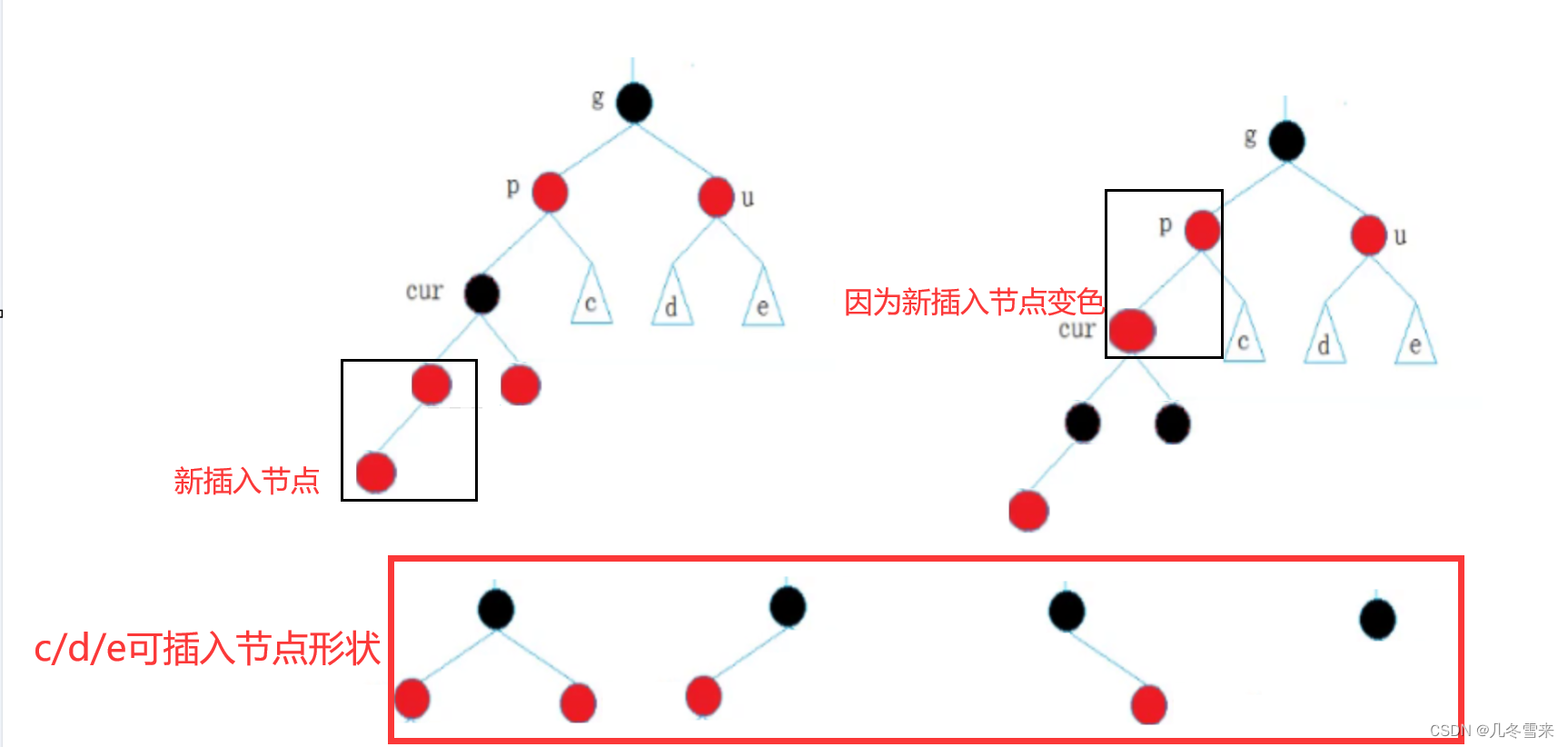
在这里的c，d，e处如果是只有一个黑节点的局部树的话有4种节点形状的插入，外加上新插入的节点有4个位置能插入，因此能计算出来这里最后能有256种（4*4*4*4）插入的结果。

并且从上图我们也可以看出来使得上下两个节点都变为红色的不止只有新插入节点的情况，也可能是新插入的节点使得grandfather变为红色，让grandfather和它的父节点颜色相同。

因此红黑树在这里有无数种组合情况。

知道红黑树在什么情况下要对其节点进行变色，在什么情况下要对其节点进行旋转操作后，接下来我们就来书写它的代码。

因为在红黑树中我们可能要不断的向上处理，首先就是一个循环判断新插入节点的父节点存不存在，存在的同时它的颜色是不是为红色，只有同时满足两个条件才能进入循环。

接下来就是确定父节点的父节点，接下来如果parent节点为grandfather节点的左边的话，这个地方我们就能确定uncle节点的位置。

再下来还是判断，如果uncle节点存在且为红色的话，这个地方我们就将parent与uncle节点更改为黑色，再将grandfather节点更改为红色。

如果第一次变色结束后修改后的parent节点不存在或者存在但是为黑的话，这里的做法就是将根节点的颜色改为黑色。

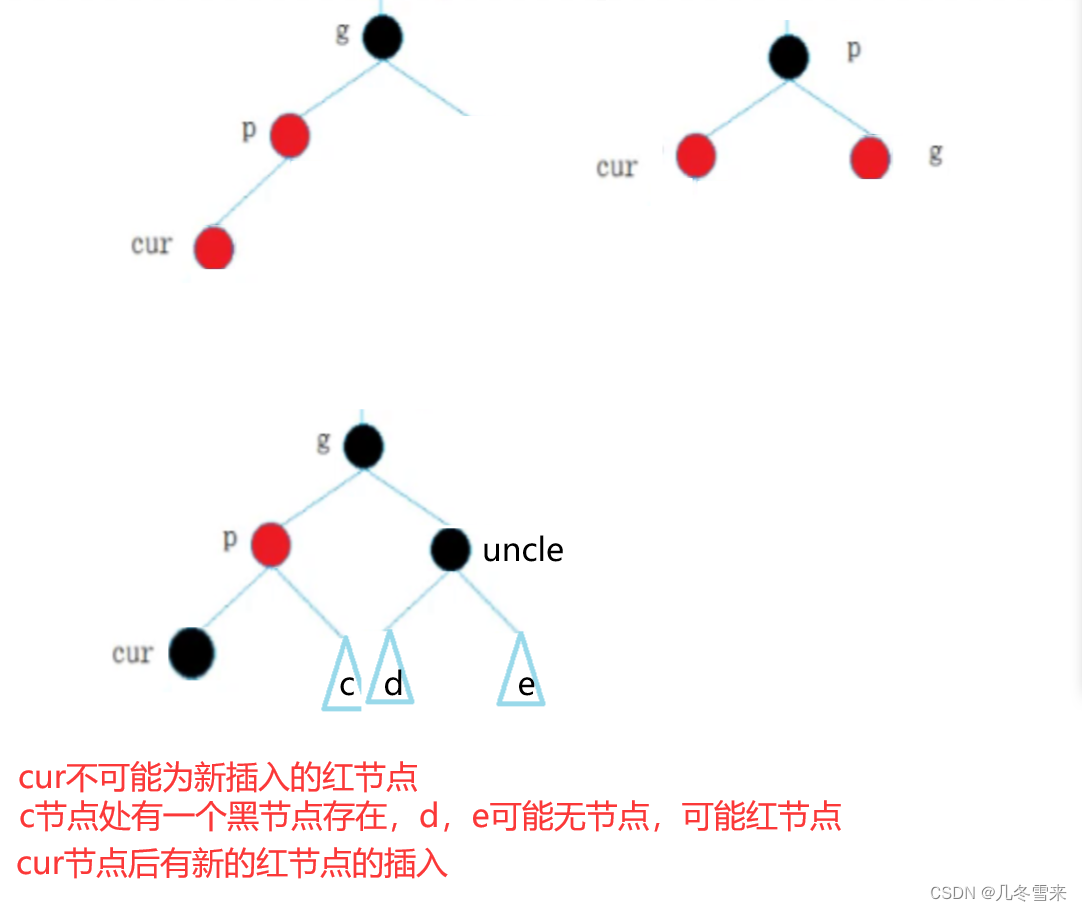
接下来就是几种比较特殊的情况，上图这种就是uncle节点不存在的情况，这种情况就需要进行旋转操作。

而下面的则是存在uncle，但是parent节点为红uncle节点的颜色为黑色的情况。在这种情况下cur节点不可能为新插入的节点，因为这会导致它们路径上的黑节点不同。

与此同时，c处应该是有一个黑色节点的局部树，d与e两个位置可以为红节点也可以为空。

并且这里旋转的代码可以从AVL树那边CV过来，唯一需要更改的就是将平衡因子删除。

这个地方在原parent为grandfather的左节点的基本上进行判断，这里如果uncle不存在或者uncle节点为黑，对其进行分类讨论。

如果parent为grandfather的左节点，cur也为parent的左节点，这里就像AVL树一样，以grandfather为旋转点进行一次右旋，而后将parent与grandfather的节点颜色进行更改。

如果cur为parent的右节点，这里也是和AVL树一样进行双旋后再对节点颜色进行更改。

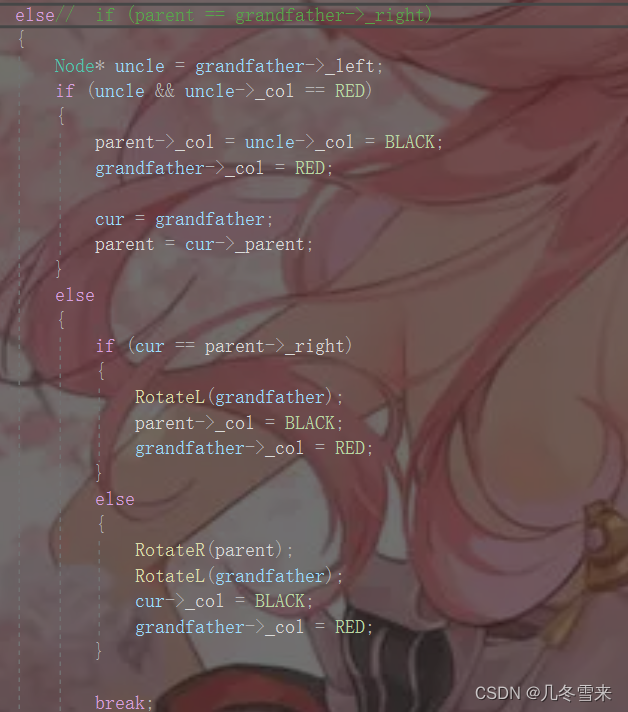
在上面我们就以parent为grandfather的左节点写了变色和处理的办法。

这个地方则继续写出当parent为grandfather的右节点的代码，其变化和旋转的方法不变，唯一变化的则是方向可能会发生改变。

判断是否为红黑树：

在书写完了红黑树之后，接下来就是一个重点知识——如何判断该树是否为红黑树，或者说改红黑树有没有错误。

就像书写AVL树一样，在代码的在最后我们也需要一个判断，判断在AVL树中它插入节点后的平衡因子会不会发生异常。

同样的红黑树也要这个操作，不同与AVL的是红黑树并没有平衡因子，而它的判断的内容则是红黑树性质的4大规则。

这里要判断的就是以上的规则：根节点是否为黑色，是否有两个红节点相连接，它每条路径的黑节点个数是否一样。

在了解完了详情之后，接下来就是对代码的书写了。

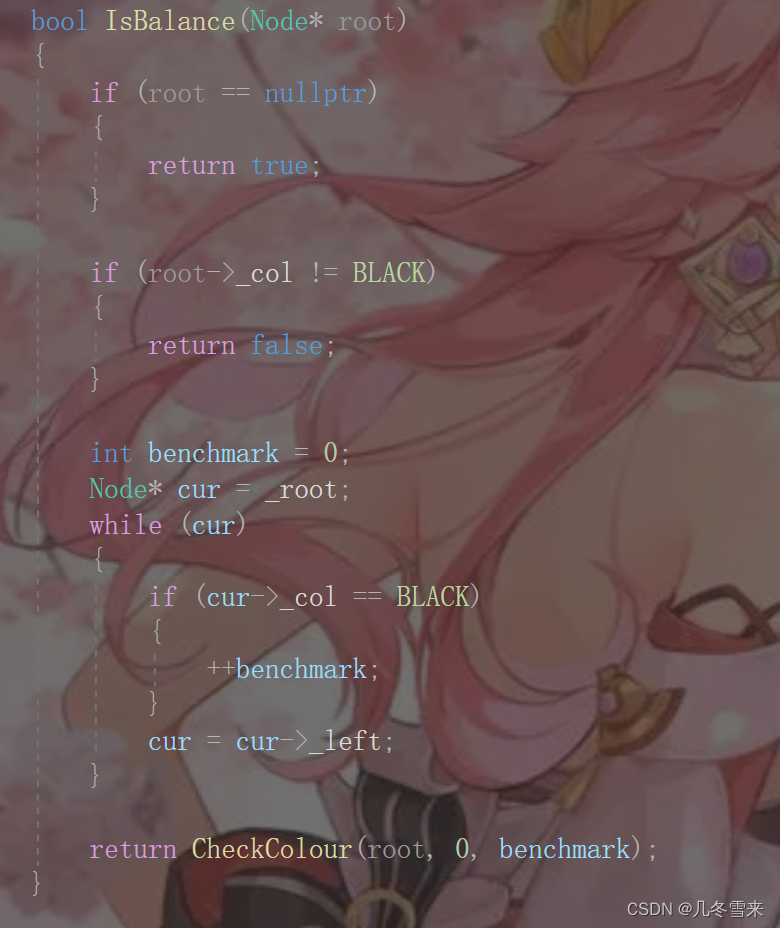
首先就是进行基础的判断，如果插入后的红黑树它的根节点为空这里就返回true，如果颜色不为黑色，这个地方就返回false。

接下来定义一个整形用来存储某条路径黑色节点的个数，这里选择的就是最左路径，统计它最左路径黑色节点的个数。

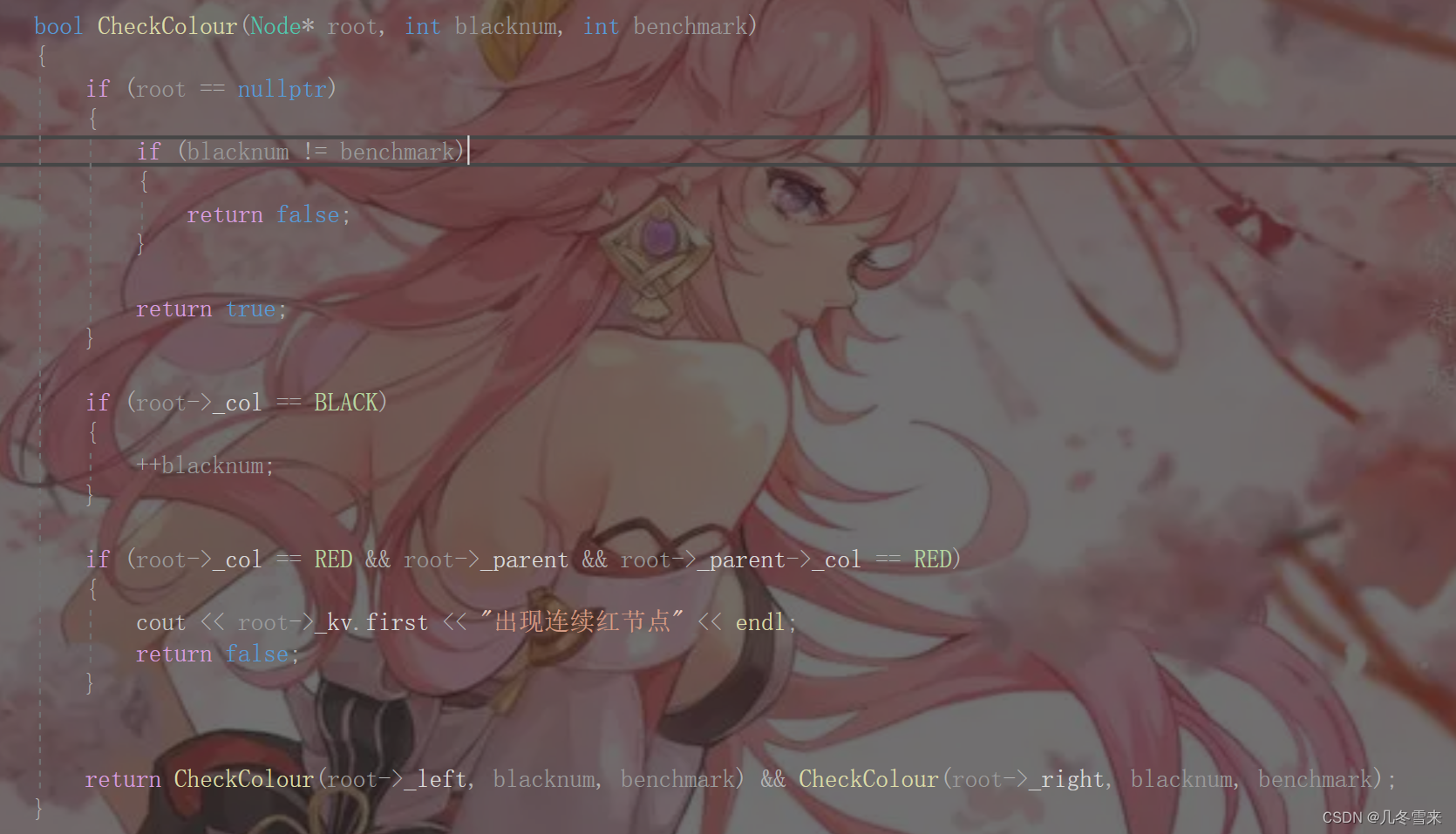
然后上面的代码就跳转到这里，也是一样先看看根节点是否为空，然后再判断里面还需要判断路径的黑色节点数是否相同（递归结束回到根节点处）。

如果root处的节点颜色为黑色，这里就对计算黑色节点的整形进行++操作。

然后就是if条件判断是否会出现连续的红节点，如果这里的root存在且为红，root的parent存在且为红，这种情况就是出现了连续的红节点，就需要报错后返回false。（这里不能用parent为红，parent的cur节点也为红的条件来判断，因为这里可能存在空节点）。

最后这里要递归root节点的左子树与右子树，递归到根节点的parent，回到开头判断各个路径黑色节点的个数是否相同。

这个地方就是我们的红黑树的判断。

代码：

RBTree.cpp

#include "RBTree.h"int main()
{int a[] = { 16,3,7,11,9 };RBTree<int, int> t;for (auto e : a){t.Insert(make_pair(e, e));cout << "Insert:" << e << "->" << t._IsBalance() << endl;}return 0;
}

RBTree.h

#pragma once
#include<iostream>
using namespace std;enum Colour
{RED,BLACK
};template<class K,class V>
struct RBTreeNode
{RBTreeNode<K, V>* _left;RBTreeNode<K, V>* _right;RBTreeNode<K, V>* _parent;pair<K, V> _kv;Colour _col;RBTreeNode(const pair<K, V>& kv):_left(nullptr),_right(nullptr),_parent(nullptr),_kv(kv),_col(RED){}
};template<class K, class V>
struct RBTree
{typedef RBTreeNode<K, V> Node;
public:bool Insert(const pair<K, V>& kv){if (_root == nullptr){_root = new Node(kv);_root->_col = BLACK;return true;}Node* cur = _root;Node* parent = nullptr;while (cur){if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else{return false;}}cur = new Node(kv);cur->_col = RED;if (parent->_kv.first < kv.first){parent->_right = cur;}else{parent->_left = cur;}cur->_parent = parent;while (parent && parent->_col == RED){Node* grandfather = parent->_parent;if (parent == grandfather->_left){Node* uncle = grandfather->_right;if (uncle && uncle->_col == RED){parent->_col = uncle->_col = BLACK;grandfather->_col = RED; cur = grandfather;parent = cur->_parent;}else{if (cur == parent->_left){RotateR(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else{RotateL(parent);RotateR(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;}}else//	if (parent == grandfather->_right){Node* uncle = grandfather->_left;if (uncle && uncle->_col == RED){parent->_col = uncle->_col = BLACK;grandfather->_col = RED;cur = grandfather;parent = cur->_parent;}else{if (cur == parent->_right){RotateL(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else{RotateR(parent);RotateL(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;}}}_root->_col = BLACK;return true;}void RotateL(Node* parent){Node* cur = parent->_right;Node* curleft = cur->_left;Node* ppnode = parent->_parent;parent->_right = curleft;if (curleft){curleft->_parent = parent;}cur->_left = parent;parent->_parent = cur;if (parent == _root){_root = cur;cur->_parent = nullptr;}else{if (ppnode->_left == parent){ppnode->_left = cur;}else{ppnode->_right = cur;}cur->_parent = ppnode;}}void RotateR(Node* parent){Node* cur = parent->_left;Node* curright = cur->_right;Node* ppnode = parent->_parent;parent->_left = cur->_right;if (curright){curright->_parent = parent;}cur->_right = parent;parent->_parent = cur;if (ppnode == nullptr){_root = cur;cur->_parent = nullptr;}else{if (ppnode->_left == parent){ppnode->_left = cur;}else{ppnode->_right = cur;}cur->_parent = ppnode;}}bool CheckColour(Node* root, int blacknum, int benchmark){if (root == nullptr){if (blacknum != benchmark){return false;}return true;}if (root->_col == BLACK){++blacknum; }if (root->_col == RED && root->_parent && root->_parent->_col == RED){cout << root->_kv.first << "出现连续红节点" << endl;return false;}return CheckColour(root->_left, blacknum, benchmark) && CheckColour(root->_right, blacknum, benchmark);}bool _IsBalance(){return IsBalance(_root);}bool IsBalance(Node* root){if (root == nullptr){return true;}if (root->_col != BLACK){return false; }int benchmark = 0;Node* cur = _root;while (cur){if (cur->_col == BLACK){++benchmark;}cur = cur->_left;}return CheckColour(root, 0, benchmark);}private:Node* _root = nullptr; 
};