LeetCode 每日一题 Day 3||深度优先搜索（DFS)

1038. 从二叉搜索树到更大和树

给定一个二叉搜索树 root (BST)，请将它的每个节点的值替换成树中大于或者等于该节点值的所有节点值之和。

提醒一下，二叉搜索树满足下列约束条件：

节点的左子树仅包含键小于节点键的节点。
节点的右子树仅包含键大于节点键的节点。
左右子树也必须是二叉搜索树。

示例 1：

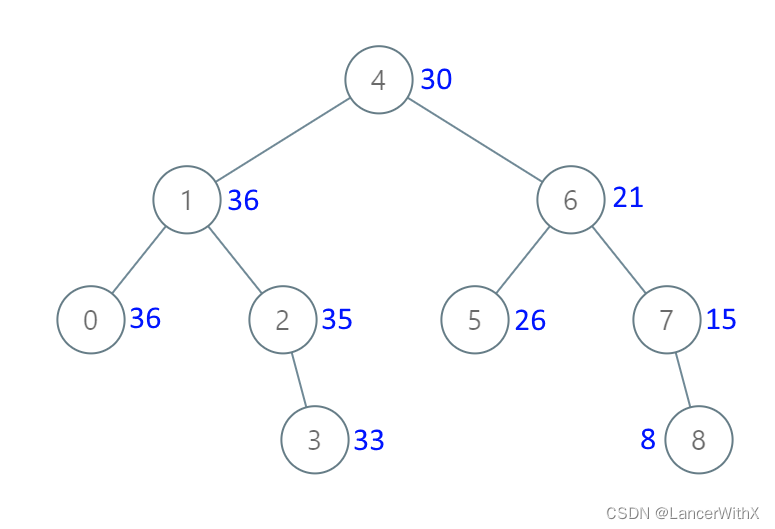
输入：[4,1,6,0,2,5,7,null,null,null,3,null,null,null,8]
输出：[30,36,21,36,35,26,15,null,null,null,33,null,null,null,8]

示例 2：

输入：root = [0,null,1]
输出：[1,null,1]
提示：

树中的节点数在 [1, 100] 范围内。
0 <= Node.val <= 100
树中的所有值均不重复。

注意：该题目与 538:把二叉搜索树转换为累加树相同

我们这里使用DFS实现，cpp代码如下：

class Solution {
public:TreeNode* bstToGst(TreeNode* root) {int sum = 0;dfs(root, sum);return root;}void dfs(TreeNode* node, int& sum) {if (node) {// 先遍历右子树dfs(node->right, sum);// 更新节点值为累加和sum += node->val;node->val = sum;// 再遍历左子树dfs(node->left, sum);}}
};

DFS

深度优先搜索（Depth-First Search，DFS）是一种用于遍历或搜索树或图的算法。在上题，DFS 用于遍历二叉搜索树（BST）的节点。

下图是一个无向图，如果我们从A点发起深度优先搜索（以下的访问次序并不是唯一的，第二个点既可以是B也可以是C,D），则我们可能得到如下的一个访问过程：A->B->E（没有路了！回溯到A)->C->F->H->G->D（没有路，最终回溯到A,A也没有未访问的相邻节点，本次搜索结束）.简要说明深度优先搜索的特点：每次深度优先搜索的结果必然是图的一个连通分量.深度优先搜索可以从多点发起.如果将每个节点在深度优先搜索过程中的"结束时间"排序（具体做法是创建一个list，然后在每个节点的相邻节点都已被访问的情况下，将该节点加入list结尾，然后逆转整个链表)，则我们可以得到所谓的拓扑排序,即topological sort.

DFS遍历

深度优先遍历图的方法是，从图中某顶点v出发：
（1）访问顶点v；
（2）依次从v的未被访问的邻接点出发，对图进行深度优先遍历；直至图中和v有路径相通的顶点都被访问；
（3）若此时图中尚有顶点未被访问，则从一个未被访问的顶点出发，重新进行深度优先遍历，直到图中所有顶点均被访问过为止。　当然，当人们刚刚掌握深度优先搜索的时候常常用它来走迷宫.事实上我们还有别的方法，那就是广度优先搜索(BFS).

也即：

判断边界，开始遍历每一种情况
选择一个起始节点作为当前节点，并将其标记为已访问。
对于当前节点的每个未访问的邻居节点，递归地进行DFS遍历。
如果当前节点没有未访问的邻居节点，回溯到上一个节点。
重复步骤2和步骤3，直到遍历完所有节点。

这两种算法的名称都非常直观，顾名思义，DFS就是一条路走到黑，直到走不动才返回重新走，而BFS则是先把所有的路都走一下，然后一层一层向下走（理解有问题的话希望大佬们指正）

具体的DFS模板：

int check(参数)
{if (满足条件) return 1;return 0;
}void dfs(int step)
{// 判断边界if (满足边界条件){// 对应操作// ...}// 遍历每一种情况for (遍历条件){if (满足check){// 标记// ...// 下一步DFSdfs(step + 1);// 回复初始状态// ...}}
}