【动态规划】LeetCode-198/LCR089.打家劫舍

🎈算法那些事专栏说明：这是一个记录刷题日常的专栏，每个文章标题前都会写明这道题使用的算法。专栏每日计划至少更新1道题目，在这立下Flag🚩
🏠个人主页：Jammingpro
📕专栏链接：算法那些事
🎯每日学习一点点，技术累计看得见

题目

题目描述

你是一个专业的小偷，计划偷窃沿街的房屋。每间房内都藏有一定的现金，影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统，如果两间相邻的房屋在同一晚上被小偷闯入，系统会自动报警。

给定一个代表每个房屋存放金额的非负整数数组，计算你不触动警报装置的情况下，一夜之内能够偷窃到的最高金额。

执行示例

示例 1：
输入：[1,2,3,1]
输出：4
解释：偷窃 1 号房屋 (金额 = 1) ，然后偷窃 3 号房屋 (金额 = 3)。
偷窃到的最高金额 = 1 + 3 = 4 。

示例2：
输入：[2,7,9,3,1]
输出：12
解释：偷窃 1 号房屋 (金额 = 2), 偷窃 3 号房屋 (金额 = 9)，接着偷窃 5 号房屋 (金额 = 1)。
偷窃到的最高金额 = 2 + 9 + 1 = 12 。

提示

1 <= nums.length <= 100
0 <= nums[i] <= 400

题解

有题目可知，由于偷盗连续的房屋将触发报警，小偷若偷窃第i家，则其不能偷窃第i-1家及i+1家，但其可以偷窃i-2家及i+2家。这种偷窃方式是“一家偷一家不偷”的方式，如下图所示↓↓↓
在这里插入图片描述
除了上面的偷窃方式，小偷可以偷完第i家后，间隔两家再偷，即“偷一家不偷不偷”的方式，如下图所示↓↓↓

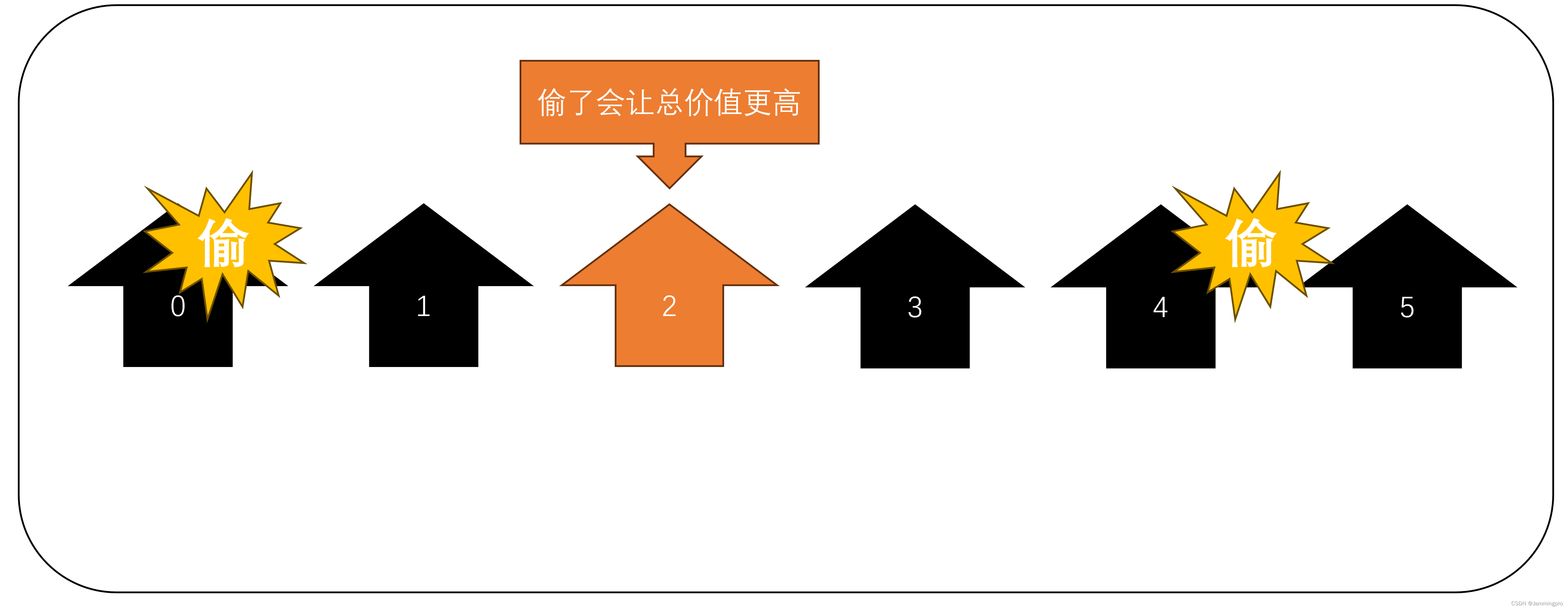
那么可不可以偷完1家，接下来的3家都不偷呢？偷一家不偷三家这种方式虽然不会出发报警，但是题目要求我们偷窃金额最大。如下图所示，小偷若偷了0号和4号房子，他还可以偷2号房子，如果不偷的话，则偷窃金额可能减小，因此必须偷。偷完1家，休息n（n≥4）家与这个同理。
在这里插入图片描述
我们另nums数组存储房子的金额，设dp表（一维数组）来存储到达第i号房子时的最大金额。则我们可以得到状态转移方程（递推公式）->dp[i]=nums[i]+max(dp[i-2],dp[i-3])。为什么是max(dp[i-2],dp[i-3])呢？因为我们偷了第i号房子，则只能偷i-2号房子及之前的房子。这里为什么只需要考虑i-2和i-3已经在前面分析过了。至此我们就可以开始编写代码了↓↓↓

class Solution {
public:int rob(vector<int>& nums) {int n = nums.size();vector<int>dp(n);dp[0] = nums[0];if(n == 1) return nums[0];dp[1] = max(nums[0], nums[1]);if(n == 2) return dp[1];dp[2] = max(nums[0] + nums[2], nums[1]);if(n == 3) return dp[2];for(int i = 3; i < n; i++)dp[i] = nums[i] + max(dp[i - 2], dp[i - 3]);return max(dp[n - 1], dp[n - 2]);}
};

这个代码在考虑n≤3时使用了许多条件语句，我们可以换个思考角度来减少这些处理操作。我们对一个房子的决策只有两种，一种是偷，一种是不偷。则此时我们可以得到另一种状态转移方程（递推公式）->dp[i]=max(dp[i-1], dp[i-2]+nums[i])，其中dp[i-1]表示不偷第i家，dp[i-2]+nums[i]表示偷第i家。因此，我们可以得到新的代码↓↓↓

class Solution {
public:int rob(vector<int>& nums) {int n = nums.size();if(n == 1) return nums[0];vector<int>dp(n);dp[0] = nums[0];dp[1] = max(nums[0], nums[1]);for(int i = 2; i < n; i++)dp[i] = max(dp[i - 1], dp[i - 2] + nums[i]);return dp[n - 1];}
};