连续性变量的组间差异分析

正态分布

正态分布检测

1：图像法

2:计算法

Shapiro–Wilk W检验（小样本推荐）

Lilliefors正态性检验

Anderson–Darling 或AD检验

D'Agostino检验（大样本推荐）

独立样本t检验

1，方差齐性检验

2，t检验

3，单侧t检验

非独立样本t检验

1，配对数据

2，配对t检验

单因素方差分析

1，单因素方差数据

2，方差齐性

3，单因素方差分析

4，可以进一步两两比较

TukeyHSD函数

Bonferroni法

非正态分布

Wilcoxon秩和检验（独立t）

Wilcoxon符号检验（配对t）

Kruskal-Wallis检验(单因素方差)

PMCMRplus包（非参数两两比较）

t检验（连续变量）和卡方检验（分类变量）-CSDN博客

正态分布

正态分布检测

1：图像法

##连续变量的统计分析##
rm(list = ls())
library(ggpubr)
data <- iris##鸢尾花数据集#查看数据分布类型
##1.1：图像法密度图
ggdensity(data$Sepal.Length, main = "Density plot",xlab = "Sepal.Length")##1.2：图像法QQ图
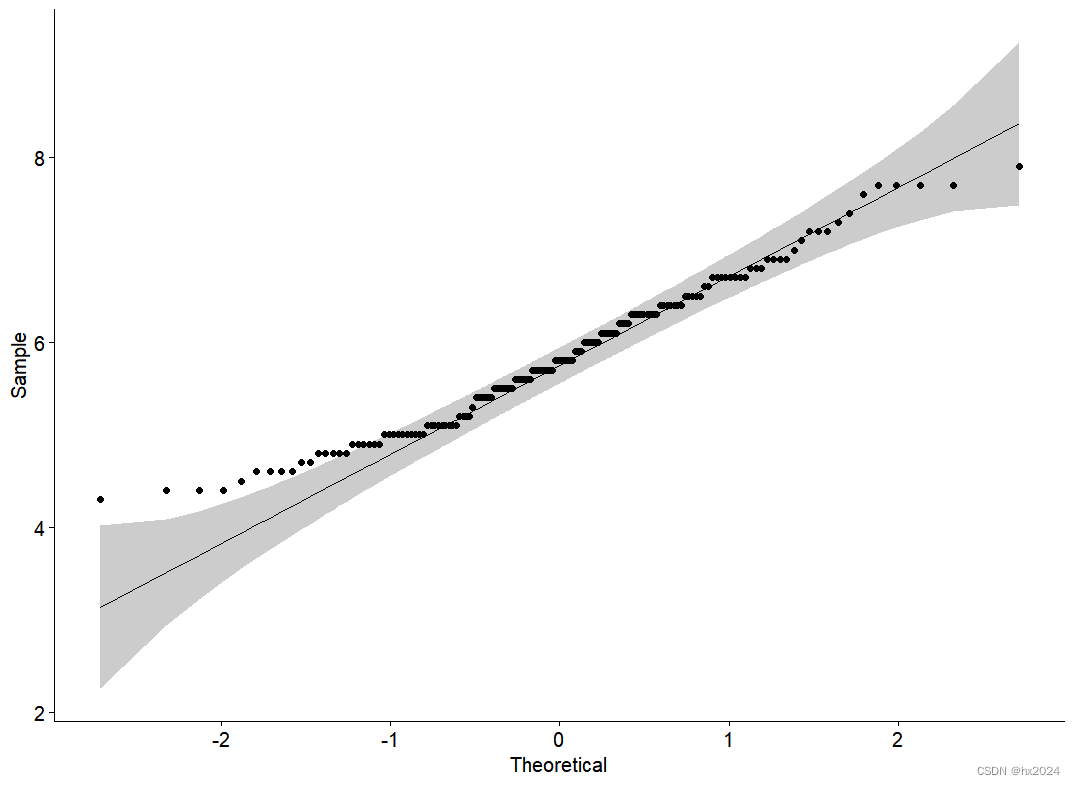
ggqqplot(data$Sepal.Length)
#定样本与正态分布之间的相关性,并给出了45度参考线，即y=x。
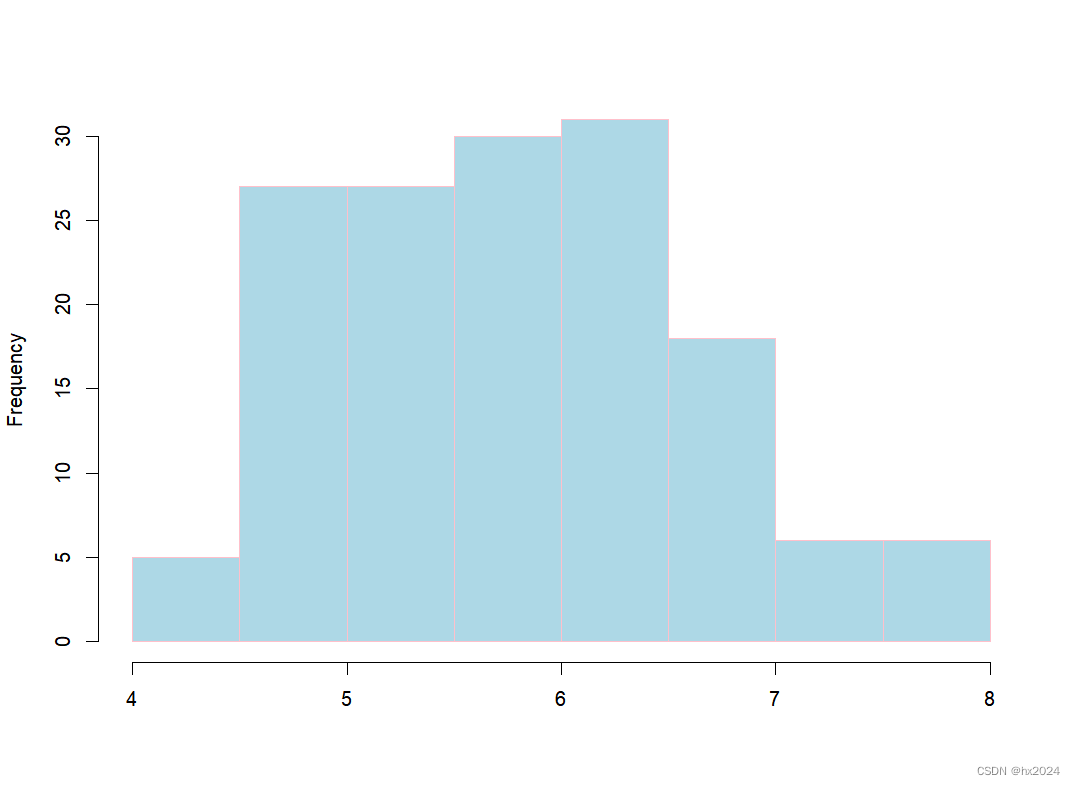
#当所有点都大致落在该参考线时，我们可以假定数据为正态。##1.3：图像法 直方图
hist(data$Sepal.Length,main = "",xlab = "", breaks = 10, col = "lightblue", border = "pink")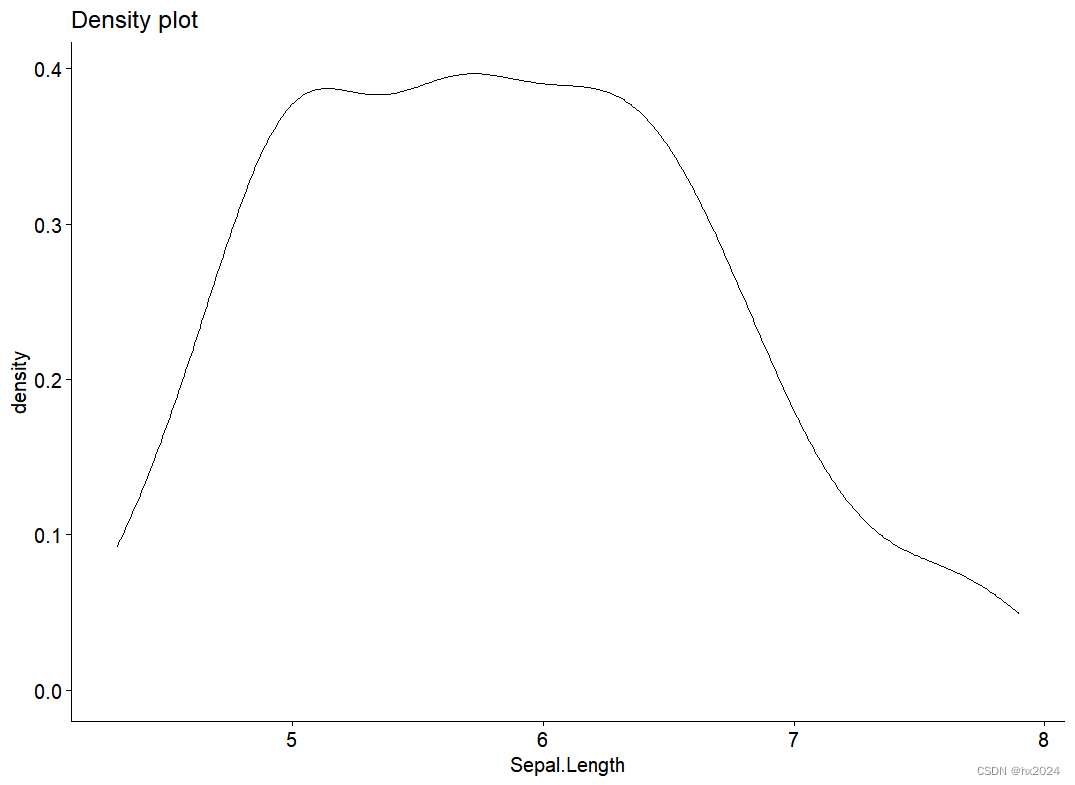

2:计算法

计算法：S.S.Shapiro&M.B.Wilk 提出的W检验法(Shapiro-Wilk检验)和 Ralaph.B.D.Agostino 提出的D检验法(D'Agostino检验)。此外，x²检验适用于任意频数分布的拟合优度检验，并非检验正态性的专用方法，效率不够高。

W检验和D检验是我国制定的正态性检验的国家标准GB4882-85推荐的正态性检验的专用方法，都需要通过专用的计算表来确定临界值；其中W检验在3≤n≤50时使用，D检验在50<n≤1000时使用。

常见检验方法介绍：

①Kolmogorov-Smirnov检验：用样本数据与期望的理论分布进行对比，如果差异不大，则可以认为数据服从正态分布。假设总体的参数是已知的，但这在实际应用中是很难做到的。

②Lilliefors正态性检验（第一个改良）：用样本均值和标准差代替总体均值和标准差。

③Anderson–Darling 或AD检验：把所有的差平方后求和，有点像计算方差。

④Shapiro–Wilk W检验：用的是经验累积概率与目标理论累积概率之差的最大值，有点像计算极差

（W检验适合于样本量在3～50之间的样本数据。有其他统计学家把其适用范围扩展到5000，因此可以说W检验几乎适用于所有的正态检验。）

R-概率统计 | 正态分布检验 - 知乎 (zhihu.com)、

R语言统计分析 01 正态性检验及方差齐性检验 - 知乎 (zhihu.com)

Shapiro–Wilk W检验（小样本推荐）

#2:Shapiro-Wilk方法
shapiro.test(data$Sepal.Length)Shapiro-Wilk normality testdata:  data$Sepal.Length
W = 0.97609, p-value = 0.01018本数据含有150个样本，超过30，且从前视觉判断，数据不存在明显的分布不均匀。视情况考虑。

假设检验H0，总体符合正态分布

W值：W越小，越接近0，表示样本数据越接近正态分布

p值：p小于显著性水平α(0.05)，表示样本数据不符合正态分布（注意使用范围）

Lilliefors正态性检验

## Lilliefor检验
library(nortest)
lillie.test(data$Sepal.Length)Lilliefors (Kolmogorov-Smirnov) normality testdata:  data$Sepal.Length
D = 0.088654, p-value = 0.005788

原假设 H0：样本服从正态分布；备择假设 H1：样本不服从正态分布。

P值>指定水平0.05,接受原假设，可以认为样本数据服从正态分布

P值<指定水平0.05,拒绝原假设，认为样本数据在5%的显著性水平下不服从正态分布

Anderson–Darling 或AD检验

#Performs the Anderson-Darling test 
#for the composite hypothesis of normality
ad.test(data$Sepal.Length)Anderson-Darling normality testdata:  data$Sepal.Length
A = 0.8892, p-value = 0.02251

零假设H0：数据服从正态分布

备择假设H1：数据不服从正态分布

P＜0.05，要拒绝原假设，说明数据是不服从正态分布。

D'Agostino检验（大样本推荐）

#D'Agostino skewness test
library(moments)
agostino.test(data$Sepal.Length, alternative = "two.sided")D'Agostino skewness testdata:  data$Sepal.Length
skew = 0.31175, z = 1.59630, p-value = 0.1104
alternative hypothesis: data have a skewness原假设为符合正态分布，认为是正态分布

CSDN博主「Pterosaur_Zero」

（1）由于每个正态性检验方法的检验角度不同，因此同一批数据用不同的检验方法可能得到的结果会不尽相同，所以在实际操作中可以根据样本量大小选择多种检验方法进行正态性检验，同时通过QQ图等图示法辅助判断；

（2）正态性检验只是检验样本数据来自正态分布总体的可能性有多大，或者说只是检验样本数据的总体是否近似正态分布，因此样本的总体并不是一定服从标准正态分布，但已有大量实验表明，即使总体仅为近似的正态分布，也能很好地进行 t -test、方差分析等参数检验。

（3）有些样本的总体可能仅为近似的正态分布，但没有一种直接的方法可以决定“偏离正态性的严重程度”是否足以改变“进行参数检验”的选择。正态性检验的意义本身并不全是为了决定什么时候使用非参数检验，还包括在确定一个样本的总体如果近似服从正态分布后，可以使用更加简单的方法来制定参考值范围、对数据进行质量控制等等。决定使用参数检验还是非参数检验是一个非常复杂且困难的问题，在实际研究中，不应该仅基于正态性检验的结果来自动断定是否使用非参数检验，还需要根据实际问题更深入地考虑其他影响因素（具体问题具体分析）。

（4）正态性检验在大多数情况下并不是十分有用。因为在样本量很少的情况下，正态检验对于检测“非正态分布”的作用不是很大；而当样本量足够大的时候，数据是否需要严格通过正态性检验、是否需要严格服从正态分布就显得不那么重要了，因为t 检验和方差分析等对于近似正态分布数据的检测结果是非常稳定的（根据大数定律和中心极限定理，当样本量足够大时，所有分布都近似于正态分布）。因此正态性检验只是一个测试方法，用于告诉我们自己的数据偏离理想正态分布的情况是否严重到足以使以正态分布为前提条件的统计方法失效，正态性检验的结果只是一个参考。
原文链接：https://blog.csdn.net/qq_33924470/article/details/114668701

独立样本t检验

如果两个样本是从两个总体中独立抽取的，即一个样本中的元素与另一个样本中的元素相互独立，则称为独立样本(Independent Samples)。

假设变量的分布呈正态分布，针对两组的独立样本，t检验可以用于两个总体均值之间的比较。通常我们需要先用函数vartest()检查两组间是否具有方差齐性，即方差是否相等。比较吸烟组和不吸烟组产妇的新生儿体重。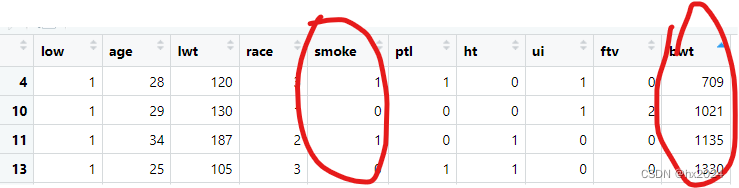

1，方差齐性检验

##连续变量的统计分析##
rm(list = ls())
library(MASS)
data <- birthwt
var.test(bwt~smoke,data =birthwt)F test to compare two variancesdata:  bwt by smoke
F = 1.3019, num df = 114, denom df = 73, p-value = 0.2254
alternative hypothesis: true ratio of variances is not equal to 1
95 percent confidence interval:0.8486407 1.9589574
sample estimates:ratio of variances 
1.301927

F = 1.3019, num df = 114, denom df = 73, p-value = 0.2254

结果表明，吸烟组和不吸烟组两组数据方差的差异没有统计学意义(p=0.2254),即组间具有方差齐性。接下来用函数t.test()进行t检验。

2，t检验

#var.equal = FALSE(默认)
t.test(bwt ~smoke,var.equal =TRUE,#这里需要选择T，前面检验相等data =birthwt)##拆开写
group1 <-birthwt$bwt[birthwt$smoke =="0"]
group2 <-birthwt$bwt[birthwt$smoke =="1"]
t.test(group1,group2,var.equal =TRUE)#一样的

	Two Sample t-testdata:  bwt by smoke
t = 2.6529, df = 187, p-value = 0.008667
alternative hypothesis: true difference in means between group 0 and group 1 is not equal to 0
95 percent confidence interval:
  72.75612 494.79735
sample estimates:
mean in group 0 mean in group 1 3055.696        2771.919

3，单侧t检验

t.test(bwt ~smoke,var.equal =TRUE,#这里需要选择T，前面检验相等alt = "greater",#设置为单侧检验（不吸烟比吸烟）conf.level = 0.95,#CI区间可以修改data =birthwt)

	Two Sample t-testdata:  bwt by smoke
t = 2.6529, df = 187, p-value = 0.004333
alternative hypothesis: true difference in means between group 0 and group 1 is greater than 0
95 percent confidence interval:106.9528      Inf
sample estimates:
mean in group 0 mean in group 1 3055.696        2771.919

非独立样本t检验

组间不是独立的：(1)同体配对，即同一受试对象分别接受两种不同处理；(2)异体配对，即两同质受试对象配成对子后分别接受两种不同的处理。在比较两组的差异时，由于组间不是独立的，需要用配对的t检验。此时，在函数t.test()里，我们需要将参数paired设为TRUE。

1，配对数据

下面建立两组数据，分别代表用脂肪酸水解法和罗紫-戈特里法对10份乳酸饮料中脂肪含量测定的结果，现欲比较两种测定结果是否存在差异。（一个样本两种方法）

x<-c(0.84,0.59,0.67,0.63,0.69,0.98,0.75,0.73,1.20,0.87)
y<-c(0.58,0.51,0.50,0.32,0.34,0.52,0.45,0.51,1.00,0.51)
data <- data.frame(x,y)
data$ID <- paste0("A",1:nrow(data))t.test(x,y,paired =TRUE)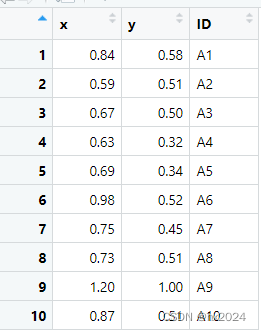

2，配对t检验

t.test(x,y,paired =TRUE)paired	
a logical indicating whether you want a paired t-test.

	Paired t-testdata:  x and y
t = 7.871, df = 9, p-value = 2.52e-05 X Y两种方法检测存在差异
alternative hypothesis: true mean difference is not equal to 0
95 percent confidence interval:0.1931133 0.3488867
sample estimates:
mean difference 0.271

单因素方差分析

多个组之间差异分析（分类>2），如果数据是从正态总体中独立抽样而得的，且满足方差齐性，我们可以用方差分析(Analysis of Variance,ANOVA)。在分类变量只有一个时，这种方差分析被称为单因素方差分析(one-way ANOVA)。

1，单因素方差数据

##数据查看：有3亚型
table(birthwt$race)
1  2  3 
96 26 67#进行正态性检验
tapply(birthwt$bwt,birthwt$race,shapiro.test)

data:  X[[i]]
W = 0.98727, p-value = 0.4861

data:  X[[i]]
W = 0.97696, p-value = 0.8038

data:  X[[i]]
W = 0.97537, p-value = 0.2046

2，方差齐性

bartlett.test()函数

bartlett.test(bwt ~race,data =birthwt)Bartlett test of homogeneity of variancesdata:  bwt by race
Bartlett's K-squared = 0.65952, df = 2, p-value = 0.7191

Bartlett检验对数据的正态性非常敏感。p-value = 0.7191 各组方差齐

3，单因素方差分析

race.aov <-aov(bwt ~race,data =birthwt)
summary(race.aov)Df   Sum Sq Mean Sq F value  Pr(>F)   
race          1  3790184 3790184   7.369 0.00726 **
Residuals   187 96179472  514329                   
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

4，可以进一步两两比较

TukeyHSD函数

需要将亚型转变为因子才能进行分析

#转换为因子
birthwt$race <- as.factor(birthwt$race)
race.aov <-aov(bwt ~race,data =birthwt)
summary(race.aov)
TukeyHSD(race.aov)Tukey multiple comparisons of means95% family-wise confidence levelFit: aov(formula = bwt ~ race, data = birthwt)$racediff       lwr        upr     p adj
2-1 -383.02644 -756.2363  -9.816581 0.0428037
3-1 -297.43517 -566.1652 -28.705095 0.0260124
3-2   85.59127 -304.4521 475.634630 0.8624372

Bonferroni法

其他进行两两比较的方法：Bonferroni法、Holm法等，这些方法的核心问题都是如何控制总的犯第一类错误的概率。

pairwise.t.test(birthwt$bwt,birthwt$race,p.adjust.method ="bonferroni")Pairwise comparisons using t tests with pooled SD data:  birthwt$bwt and birthwt$race 1     2    
2 0.049 -    
3 0.029 1.000P value adjustment method: bonferroni #从四格表中找对应的P值

多因素方差学习：R语言方差分析总结_r语言方差分析结果解读-CSDN博客

非正态分布

Wilcoxon秩和检验（独立t）

如果数据无法满足t检验(不符合正态分布)或者方差分析（方差不齐）的假设，例如变量呈明显的偏态分布，或者组间不具有方差齐性，我们可以采用非参数方法。对于两组独立样本，可以使用Wilcoxon秩和检验来评估观测值是否是从相同的分布中抽得的。

这里使用wilcox.test()测试前面数据

rm(list = ls())
library(MASS)
data <- birthwt
wilcox.test(bwt~smoke,data =birthwt)Wilcoxon rank sum test with continuity correctiondata:  bwt by smoke
W = 5249.5, p-value = 0.006768
alternative hypothesis: true location shift is not equal to 0

与上面t检验的结果相同，再次拒绝了吸烟组和非吸烟组新生儿体重相同的假设(p< 0.01)。

Wilcoxon符号检验（配对t）

Wilcoxon符号秩检验可以看作非独立样本t检验的一种非参数替代方法。

rm(list = ls())
x<-c(0.84,0.59,0.67,0.63,0.69,0.98,0.75,0.73,1.20,0.87)
y<-c(0.58,0.51,0.50,0.32,0.34,0.52,0.45,0.51,1.00,0.51)
data <- data.frame(x,y)
data$ID <- paste0("A",1:nrow(data))wilcox.test(x,y,paired = T)

Kruskal-Wallis检验(单因素方差)

对于多于两组间比较的情况，如果无法满足方差分析的假设条件，也需要借助非参数方法。如果各组之间相互独立，可以使用Kruskal-Wallis检验；如果各组之间不独立(如重复测量设计),则应该使用Friedman M检验。在R里，进行这两种检验的函数分别为kruskal.test()和friedman.test(),其使用方法类似。以Kruskal-Wallis检验为例：

kruskal.test(bwt ~race,data =birthwt)Kruskal-Wallis rank sum testdata:  bwt by race
Kruskal-Wallis chi-squared = 8.5199, df = 2, p-value = 0.01412

这个p值比用t检验得到的p值更大，这也验证了对于同样的数据，非参数检验的结论相比参数检验更为保守。

PMCMRplus包（非参数两两比较）

PMCMRplus包进行非参数方法的组间两两比较。

library(PMCMRplus)
comp <-bwsAllPairsTest(bwt ~race,data =birthwt)
summary(comp)

Pairwise comparisons using BWS All-Pairs Testdata: bwt by race
alternative hypothesis: two.sided
P value adjustment method: holm
H0B value Pr(>|B|)  
2 - 1 == 0   3.980 0.026755 *
3 - 1 == 0   3.517 0.030137 *
3 - 2 == 0   0.729 0.535124  
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

参考：

1：医学统计学/孙振球，徐勇勇主编.—4版.—北京：人民卫生出版社，2014

2：R语言医学数据分析实战/赵军编著.--北京：人民邮电出版社，2020.8