UVA437 巴比伦塔 The Tower of Babylon
题面翻译
题目描述
你可能已经听说过巴比伦塔的传说。现在这个传说的许多细节已经被遗忘。所以本着本场比赛的教育性质,我们现在会告诉你整个传说:
巴比伦人有 n n n 种长方形方块,每种有无限个,第 i i i 种方块的三边边长是 x i , y i , z i xi,yi,zi xi,yi,zi。对于每一个方块,你可以任意选择一面作为底,这样高就随着确定了。举个例子,同一种方块,可能其中一个是竖着放的,一个是侧着放的,一个是横着放的。
他们想要用堆方块的方式建尽可能高的塔。问题是,只有一个方块的底的两条边严格小于另一个方块的底的两条边,这个方块才能堆在另一个上面。这意味着,一个方块甚至不能堆在一个底的尺寸与它一样的方块的上面。
你的任务是编写一个程序,计算出这个塔可以建出的最高的高度。
输入格式
输入会包含至少一组数据,每组数据的第一行是一个整数 n ( n ≤ 30 ) n(n\le30) n(n≤30),表示方块的种类数。 这组数据接下来的 n n n 行,每行有三个整数,表示 x i , y i , z i xi,yi,zi xi,yi,zi。输入数据会以 0 0 0 结束。
输出格式
对于每组数据,输出一行,其中包含组号(从 1 1 1 开始)和塔最高的高度。按以下格式:Case i: maximum height = __。
题目描述

输入格式

输出格式
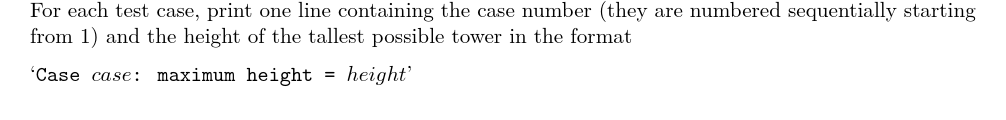
样例 #1
样例输入 #1
1
10 20 30
2
6 8 10
5 5 5
7
1 1 1
2 2 2
3 3 3
4 4 4
5 5 5
6 6 6
7 7 7
5
31 41 59
26 53 58
97 93 23
84 62 64
33 83 27
0
样例输出 #1
Case 1: maximum height = 40
Case 2: maximum height = 21
Case 3: maximum height = 28
Case 4: maximum height = 342
Solution
因为方块数目不限,每一个方块有长宽高三个参数,方块放置有6种方式分别为:
- x,y,z
- y,x,z
- y,z,x
- z,y,x
- z,x,y
- x,z,y
设dp[i]表示第i个方块可以放置的最大高度,则可以建立状态转移方程,在满足一个方块的底的两条边严格小于另一个方块的底的两条边的情况下,有状态转移方程dp[i] = max(dp[j] + blocks[i].getHigh(), dp[i]);
其中对blocks进行排序是因为只有保证上层的块的底面积严格小于下层的块的时候,才可以将上层的块放到下层的块上
//
// Created by Gowi on 2023/11/24.
//#include <iostream>
#include <cstring>
#include <algorithm>#define N 200using namespace std;class block {
private:int x, y, z, area, high;
public:block() {};block(int a, int b, int c) {x = a;y = b;z = c;area = a * b;high = c;}bool operator<(block a) const {return this->area <= a.area;}int getX() const {return x;}void setX(int x) {block::x = x;}int getY() const {return y;}void setY(int y) {block::y = y;}int getZ() const {return z;}void setZ(int z) {block::z = z;}int getArea() const {return area;}void setArea(int area) {block::area = area;}int getHigh() const {return high;}void setHigh(int high) {block::high = high;}
};int n, t;
block blocks[N];
int dp[N];bool init() {t = 0;cin >> n;if (n == 0) {return false;}memset(blocks, 0, sizeof(blocks));memset(dp, 0, sizeof(dp));for (int i = 0; i < n; ++i) {int a, b, c;cin >> a >> b >> c;blocks[t++] = block(a, b, c);blocks[t++] = block(b, a, c);blocks[t++] = block(b, c, a);blocks[t++] = block(c, b, a);blocks[t++] = block(c, a, b);blocks[t++] = block(a, c, b);}sort(blocks, blocks + t);return true;
}int main() {int k = 0;while (init()) {int maxheight = 0;for (int i = t - 1; i >= 0; i--) {dp[i] = blocks[i].getHigh();for (int j = t - 1; j >= 0; j--) {if (blocks[i].getX() < blocks[j].getX() && blocks[i].getY() < blocks[j].getY()) {dp[i] = max(dp[j] + blocks[i].getHigh(), dp[i]);}}if (dp[i] > maxheight) {maxheight = dp[i];}}cout << "Case " << ++k << ": maximum height = " << maxheight << endl;}return 0;
}











边界布局,网格布局)
)




:系统设计与分析的关键视觉工具)
