这个标题涉及到电力系统领域的一些关键概念和方法。让我们逐步解读：

1. 基于Fisher时段划分：

   • "基于"表示这个策略或方法的核心基础是某个特定的理论或技术。
   • "Fisher时段划分"可能指的是使用Fisher信息矩阵进行时间划分。Fisher信息矩阵是一种在统计学和信息论中使用的工具，用于衡量概率分布的不确定性。

2. 配电网：

   • 这指的是电力系统中的一个部分，主要负责将电力从输电网引入各个用户和终端设备。

3. 源网荷储：

   • "源"可能指的是电力的来源，可以是传统的发电机或者可再生能源。
   • "网"通常指的是电力网络。
   • "荷"是负荷，即电力系统中实际消耗电能的设备。
   • "储"可能指的是能量储存系统，比如电池。

4. 多时间尺度：

   • 这意味着该策略或方法考虑了多个时间尺度，可能包括短时段、中时段和长时段。这是因为电力系统具有各种时间尺度上的变化，从瞬时的电压波动到日/夜周期性变化以及季节性变化。

5. 协调优化调控策略：

   • "协调"表明这是一个综合考虑多个因素的策略。
   • "优化"意味着该策略通过数学模型或算法来找到系统性能的最佳配置。
   • "调控"涉及到对电力系统进行实时或计划内的调整，以满足用户需求或确保系统的稳定性。

综合起来，这个标题可能描述了一种电力系统管理的策略，该策略基于Fisher信息矩阵的时间划分方法，考虑了配电网中源、网、荷、储的多个时间尺度上的协调优化调控。这种方法可能有助于提高电力系统的效率、稳定性和可靠性。

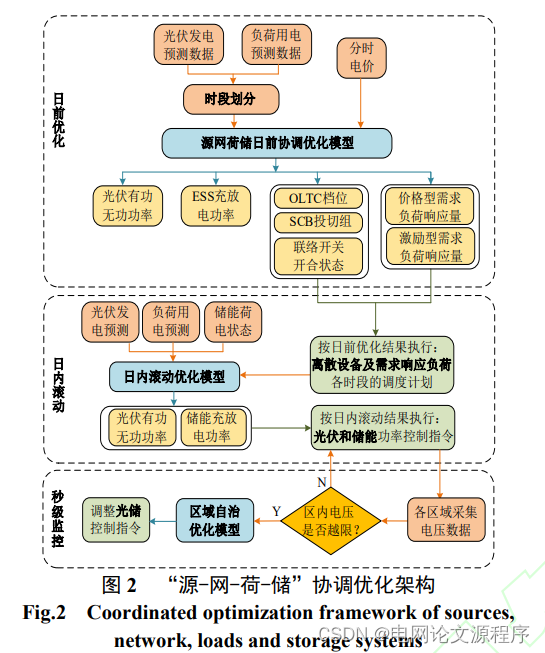
摘要：多元可控资源的联合优化调控对于提高配电网运行安全性和经济性意义重大，但同时大幅增加优化问题复杂度，降低模型求解效率。基于此，本文提出了基于Fisher时段划分的配电网源-网-荷-储协调优化调控策略。首先，构建多时间尺度“源网荷储”协调优化架构，包括日前优化、日内滚动和秒级监控三个阶段。其次，研究基于源荷功率区间数据的Fisher最优分割时段划分方法。然后，建立日前优化调控模型、日内滚动优化模型和区域自治优化模型，求解电网离散设备、需求响应负荷、光伏和储能等的最优调控指令。最后，以IEEE 33节点系统为例，对所提协调优化调控策略进行仿真验证。算例结果表明，所提方法能够大幅提高协调优化模型的计算效率，并保证电网运行安全性和经济性。

这段摘要涉及到一项研究，该研究关注电力系统中多元可控资源的联合优化调控，旨在提高配电网的运行安全性和经济性。以下是对摘要的详细解读：

1. 研究目标：

   • 目标是提高配电网运行安全性和经济性，通过联合优化调控多元可控资源。

2. 挑战和问题：

   • 强调了一个普遍问题，即联合优化调控增加了问题的复杂性，可能降低了模型求解效率。

3. 提出的策略：

   • 提出了一种基于Fisher时段划分的协调优化调控策略。

4. 方法概述：

   • 构建了一个多时间尺度的协调优化架构，包括日前优化、日内滚动和秒级监控三个阶段。这意味着该策略考虑了不同时间尺度上的优化问题，从长期计划到实时监控。
   • 使用了基于源荷功率区间数据的Fisher最优分割时段划分方法，该方法可能有助于降低优化问题的复杂性。

5. 模型细节：

   • 建立了日前优化调控模型、日内滚动优化模型和区域自治优化模型。
   • 这些模型用于求解电网离散设备、需求响应负荷、光伏和储能等的最优调控指令。

6. 仿真验证：

   • 以IEEE 33节点系统为例，对所提出的协调优化调控策略进行了仿真验证。
   • 算例结果表明，该方法在大幅提高协调优化模型的计算效率的同时，保证了电网运行的安全性和经济性。

总体而言，该研究通过引入Fisher时段划分和多时间尺度的优化架构，提出了一种能够有效解决电力系统复杂性问题的协调优化调控策略。通过仿真验证，研究者展示了这种策略在实际系统中的有效性。

关键词:主动配电网; 时段划分;源_网-荷-储; 优化调控;

这些关键词涉及到电力系统和优化调控方面的重要概念。以下是对这些关键词的解读：

1. 主动配电网:

   • "主动"表明这是一种具有主动性质的配电网，可能意味着它能够主动调整和管理电力流动，而不仅仅是被动地传输电能。
   • "配电网"是指将电力从输电网引入各个用户和终端设备的网络。

2. 时段划分:

   • 这指的是将时间分割成不同的时段，可能是为了更好地适应电力系统的不同运行状态。
   • 在这个上下文中，可能是使用Fisher信息矩阵等方法进行时段划分。

3. 源-网-荷-储:

   • "源"通常指电力的来源，可以包括传统的发电机、可再生能源等。
   • "网"是指电力网络，包括输电网和配电网。
   • "荷"是负荷，即实际消耗电能的设备。
   • "储"可能指能量储存系统，如电池。

4. 优化调控:

   • "优化"表明这涉及到通过数学模型或算法来找到系统性能的最佳配置。
   • "调控"涉及到对电力系统进行实时或计划内的调整，以满足用户需求或确保系统的稳定性。

综合而言，这些关键词一起描述了一种具有主动性质的配电网系统，该系统通过时段划分考虑了不同时间段内的源、网、荷和储的协调优化调控。这可能涉及到对电力系统进行综合管理，以提高其效率、稳定性和经济性。

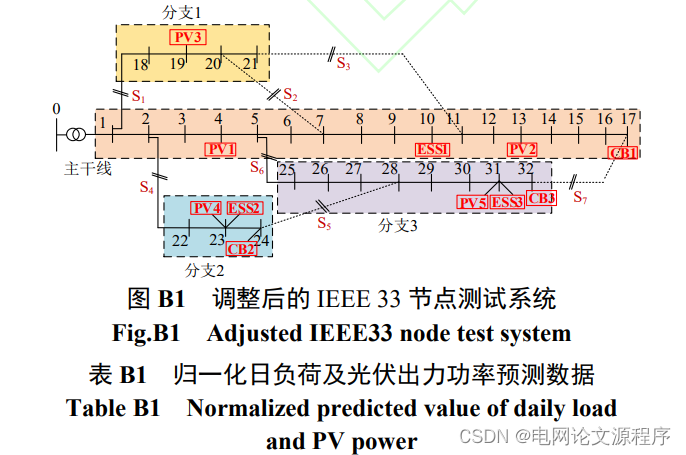
仿真算例：本文采用调整的 IEEE 33 节点配电系统对所提源网荷储协调优化调控策略的可行性和有效性进行仿真验证。系统拓扑图如附录图 B1 所示，基准容量设为 10MVA，基准电压为 12.66kV。平衡节点0 的电压幅值设为 1.03pu，有载调压变压器两侧电压变比的可调范围为 0.95~1.05pu，变比调节步长为0.0125pu。系统包含 7 个馈线开关 S1~S7，设定馈线开关的初始状态为 S1、S4 和 S6 闭合而其他开关断开。在秒级监控阶段，系统分为一个主干线和三个分支线共 4 个区域进行自治优化，如附录图 B1 所示。各节点负荷的预测数据参考文献[26]。节点 4、13、19、23 和 31 接入光伏系统，其中节点 4 和 31的光伏装机容量均为 0.8MVA，节点 13 光伏装机1MVA，节点 19 和 23 光伏装机 1.5MVA。归一化的日负荷及光伏发电功率预测数据见附录表 B1。节点 10、23 和 31 接入储能系统，容量均为 2MWh，最大充放电功率为其容量的 15%。节点 17、24 和32 接入并联电容器组，无功补偿范围为 0~500kvar。节点 6 和 23 的激励型需求响应负荷可直接控制，其时序负荷功率及最大削减量见附录表 B2。节点18和31的电价型需求响应负荷参与分时电价响应，其负荷数据及最大平移量见附录表 B3。本文参考文献[27]和[28]设定各可控资源的补偿成本和分时电价，分别如附录表 B4 和附录表 B5 所示。

仿真程序复现思路：

复现这篇文章的仿真涉及到建立一个能够模拟 IEEE 33 节点配电系统，并实施源网荷储协调优化调控策略的仿真环境。由于文章中没有具体提到使用哪种仿真工具或语言，以下是一种可能的复现思路，以Python为例，使用相关库进行仿真。

1. 建立系统模型：
   • 使用相关库（如NetworkX）建立 IEEE 33 节点配电系统的拓扑图。
   • 设定节点参数，包括基准容量、基准电压、节点负荷等。

import networkx as nx# 创建图
G = nx.Graph()# 添加节点
G.add_nodes_from(range(33))# 添加边（具体边的连接关系根据附录图 B1 设定）
G.add_edges_from([(1, 2), (2, 3), ...])# 设置节点参数
nx.set_node_attributes(G, {0: {'voltage_amplitude': 1.03}, 1: {'load': ...}, ...})

1. 设定系统初始状态：
   • 根据文章描述，设定初始状态，包括馈线开关状态、光伏系统容量、储能系统容量等。

# 设定馈线开关初始状态
switch_states = {1: 'closed', 4: 'closed', 6: 'closed', ...}# 设定光伏系统容量
pv_capacity = {4: 0.8, 31: 0.8, 13: 1, 19: 1.5, 23: 1.5}# 设定储能系统容量
storage_capacity = {10: 2, 23: 2, 31: 2}

1. 执行仿真：
   • 制定仿真算法，按照秒级监控阶段的自治优化划分系统区域。
   • 在每个时间步内，更新系统状态，考虑光伏发电、储能系统的充放电、激励型需求响应、电价型需求响应等。

# 在每个时间步内更新系统状态
for timestep in range(total_timesteps):# 执行优化调控策略，更新系统状态update_system_state(G, switch_states, pv_capacity, storage_capacity, ...)# 记录仿真结果record_simulation_results(G, timestep, ...)# 仿真结束后，进行结果分析和可视化
analyze_and_visualize_results(G, ...)

1. 结果分析和可视化：
   • 使用相关库（如Matplotlib、Pandas等）对仿真结果进行分析和可视化。

import matplotlib.pyplot as plt
import pandas as pd# 可以根据仿真结果的数据结构调整以下示例
results_df = pd.DataFrame(simulation_results)# 可视化结果
plt.plot(results_df['timestep'], results_df['node_voltage'])
plt.xlabel('Timestep')
plt.ylabel('Node Voltage')
plt.title('Simulation Results')
plt.show()

以上只是一个简化的示例，具体的仿真过程和算法需要根据文章中提供的详细信息进行具体设计。