738. Monotone Increasing Digits
An integer has monotone increasing digits单调递增数字 if and only if each pair of adjacent digits x and y satisfy x <= y.
Given an integer n, return the largest number that is less than or equal to n with monotone increasing digits.

violent solution:
Time complexity: O(n × m) m is the length of the number n
Space complexity: O(1)
class Solution:def monotoneIncreasingDigits(self, n: int) -> int:for i in range(n, -1, -1):if self.check_num(i):return i#return 0def check_num(self, n):max = 10while n:t = n % 10if max >= t:max = telse:return Falsen = n//10return True
greedy:
1. A local optimum leads to a global
2. traversal from right to the left
class Solution:def monotoneIncreasingDigits(self, n: int) -> int:n_str = list(str(n))for i in range(len(n_str) - 1, 0, -1):if n_str[i] < n_str[i - 1]: #string can compare the value, but you can still use int()n_str[i - 1] = str(int(n_str[i - 1]) - 1)for j in range(i, len(n_str)):n_str[j] = '9'return int(''.join(n_str))Time complexity: O(n), n is the length of the number
Space complexity: O(n), need a string, it is more convenient to convert to string operation
968. Binary Tree Cameras
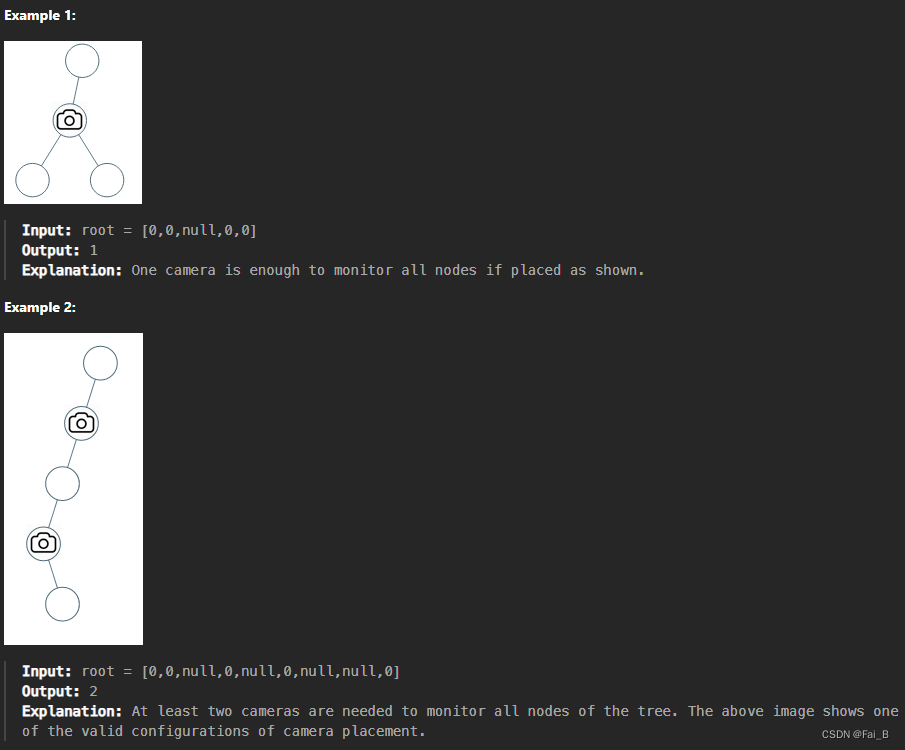
You are given the root of a binary tree. We install cameras on the tree nodes where each camera at a node can monitor监控 its parent, itself, and its immediate children.
Return the minimum number of cameras needed to monitor all nodes of the tree.
Local optimization: let the parent of a leaf node plant a camera, the least number of cameras used.
Overall optimization: minimize the number of cameras used for all.
Case 1: Both left and right nodes are covered
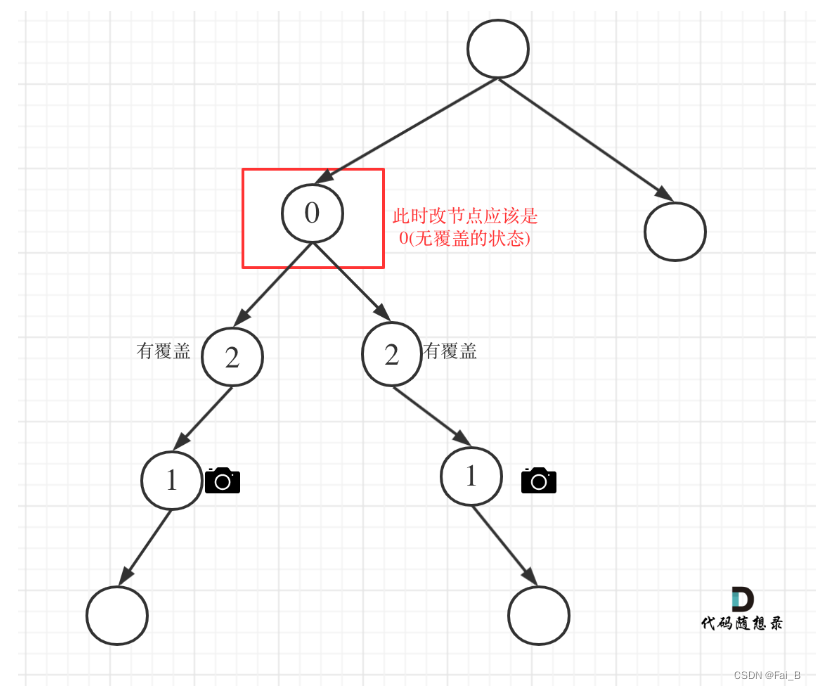
Case 2: At least one of the left and right nodes is uncovered
Case 3: At least one of the left and right nodes has a camera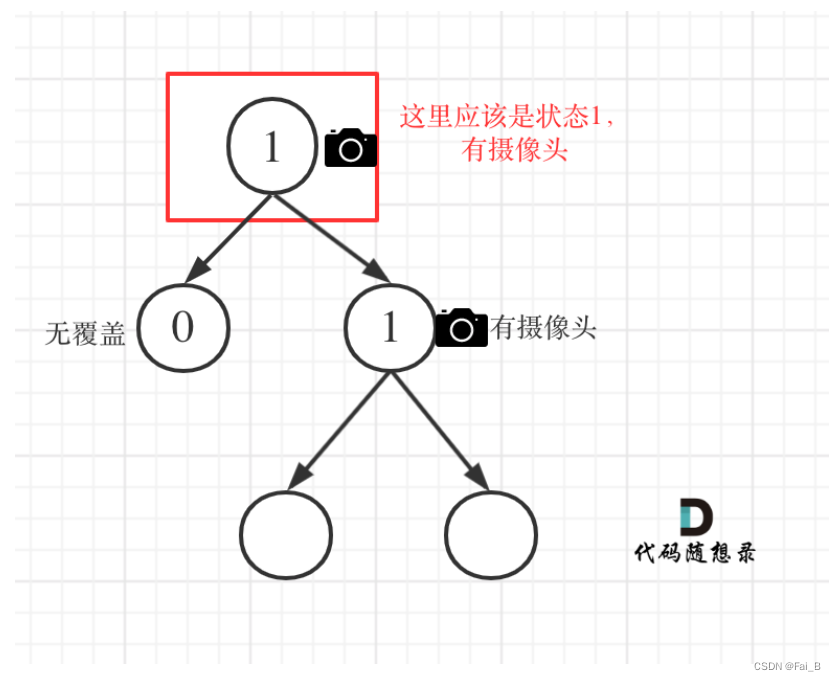
Case 4: Header node not covered
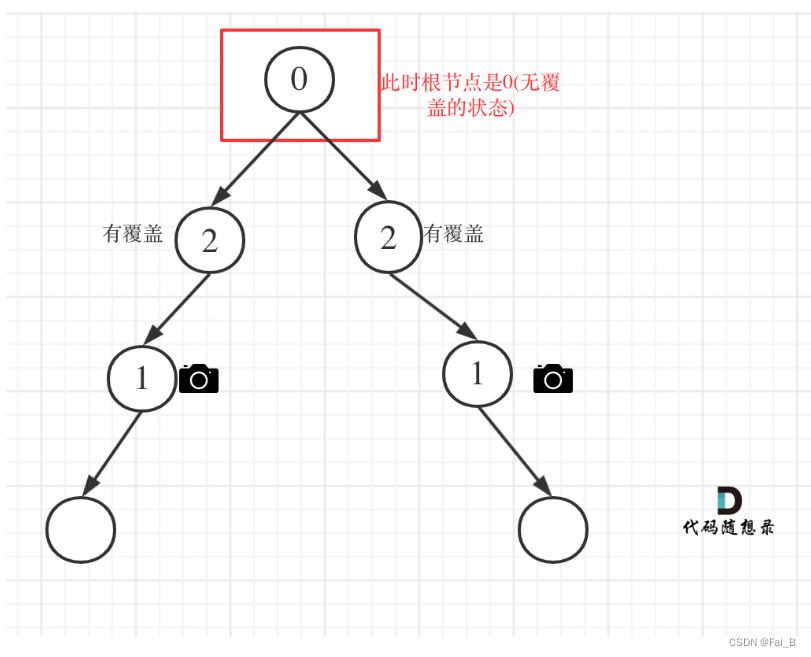
class Solution:# Greedy Algo:# 从下往上安装摄像头:跳过leaves这样安装数量最少,局部最优 -> 全局最优# 先给leaves的父节点安装,然后每隔两层节点安装一个摄像头,直到Head# 0: 该节点未覆盖# 1: 该节点有摄像头# 2: 该节点有覆盖def minCameraCover(self, root: TreeNode) -> int:# 定义递归函数result = [0] # 用于记录摄像头的安装数量if self.traversal(root, result) == 0:result[0] += 1return result[0]def traversal(self, cur: TreeNode, result: List[int]) -> int:if not cur:return 2left = self.traversal(cur.left, result)right = self.traversal(cur.right, result)# 情况1: 左右节点都有覆盖if left == 2 and right == 2:return 0# 情况2:# left == 0 && right == 0 左右节点无覆盖# left == 1 && right == 0 左节点有摄像头,右节点无覆盖# left == 0 && right == 1 左节点无覆盖,右节点有摄像头# left == 0 && right == 2 左节点无覆盖,右节点覆盖# left == 2 && right == 0 左节点覆盖,右节点无覆盖if left == 0 or right == 0:result[0] += 1return 1# 情况3:# left == 1 && right == 2 左节点有摄像头,右节点有覆盖# left == 2 && right == 1 左节点有覆盖,右节点有摄像头# left == 1 && right == 1 左右节点都有摄像头if left == 1 or right == 1:return 2










)






)

