文章目录
机器学习专栏
无监督学习介绍
聚类
K-Means
使用方法
实例演示
代码解析
绘制决策边界
本章总结
机器学习专栏
机器学习_Nowl的博客-CSDN博客

无监督学习介绍
某位著名计算机科学家有句话:“如果智能是蛋糕,无监督学习将是蛋糕本体,有监督学习是蛋糕上的糖霜,强化学习是蛋糕上的樱桃”
现在的人工智能大多数应用有监督学习,但无监督学习的世界也是广阔的,因为如今大部分的数据都是没有标签的
上一篇文章讲到的降维就是一种无监督学习技术,我们将在本章介绍聚类
聚类
聚类是指发现数据集中集群的共同点,在没有人为标注的情况下将数据集区分为指定数量的类别
K-Means
K-Means是一种简单的聚类算法。能快速,高效地对数据集进行聚类
使用方法
from sklearn.cluster import KMeansmodel = KMeans(n_clusters=3)
model.fit(data)这段代码导入了KMeans机器学习库,指定模型将数据划分为三类
实例演示
import numpy as np
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt# 生成一些随机数据作为示例
np.random.seed(42)
data = np.random.rand(100, 2) # 100个数据点,每个点有两个特征# 指定要分成的簇数(可以根据实际情况调整)
num_clusters = 3# 使用KMeans算法进行聚类
kmeans = KMeans(n_clusters=num_clusters)
kmeans.fit(data)# 获取每个数据点的所属簇标签
labels = kmeans.labels_# 获取每个簇的中心点
centroids = kmeans.cluster_centers_print(centroids)
# # 可视化结果
for i in range(num_clusters):cluster_points = data[labels == i]plt.scatter(cluster_points[:, 0], cluster_points[:, 1], label=f'Cluster {i + 1}')# 绘制簇中心点
plt.scatter(centroids[:, 0], centroids[:, 1], marker='X', s=200, color='red', label='Centroids')plt.scatter(centroids[0][0], centroids[0][1])plt.title('K-means Clustering')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.legend(loc='upper right')
plt.show()
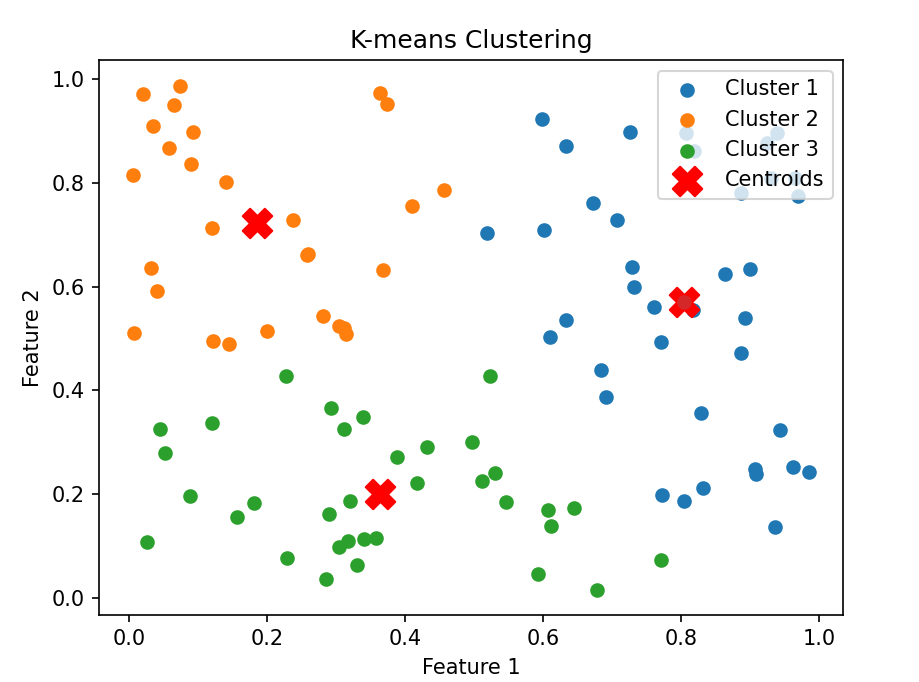
代码解析
-
导入必要的库: 导入NumPy用于生成随机数据,导入
KMeans类从scikit-learn中进行K-means聚类,导入matplotlib.pyplot用于可视化。 -
生成随机数据: 使用NumPy生成一个包含100个数据点的二维数组,每个数据点有两个特征。
-
指定簇的数量: 将
num_clusters设置为希望的簇数,这里设置为3。 -
应用K-means算法: 创建
KMeans对象,指定簇的数量,然后使用fit方法拟合数据。模型训练完成后,每个数据点将被分配到一个簇,并且簇中心点将被计算。 -
获取簇标签和中心点: 使用
labels_属性获取每个数据点的簇标签,使用cluster_centers_属性获取每个簇的中心点。 -
可视化聚类结果: 使用循环遍历每个簇,绘制簇中的数据点。然后,使用
scatter函数绘制簇中心点,并为图添加标题、轴标签和图例。 -
显示图形: 最后,使用
show方法显示可视化结果
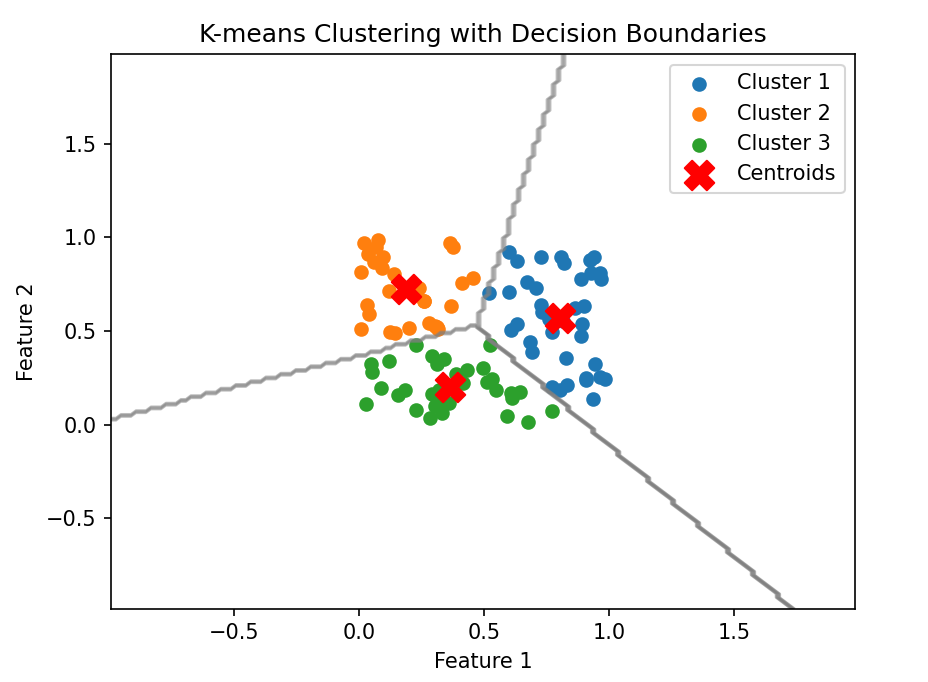
绘制决策边界
我们使用网格坐标和predict方法生成决策边界,然后使用contour函数在图上绘制边界。
主要代码
import numpy as np
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt# 生成一些随机数据作为示例
np.random.seed(42)
data = np.random.rand(100, 2) # 100个数据点,每个点有两个特征# 指定要分成的簇数(可以根据实际情况调整)
num_clusters = 3# 使用KMeans算法进行聚类
kmeans = KMeans(n_clusters=num_clusters)
kmeans.fit(data)# 获取每个数据点的所属簇标签
labels = kmeans.labels_# 获取每个簇的中心点
centroids = kmeans.cluster_centers_# 可视化结果,包括决策边界
for i in range(num_clusters):cluster_points = data[labels == i]plt.scatter(cluster_points[:, 0], cluster_points[:, 1], label=f'Cluster {i + 1}')# 绘制簇中心点
plt.scatter(centroids[:, 0], centroids[:, 1], marker='X', s=200, color='red', label='Centroids')# 绘制决策边界
h = 0.02 # 步长
x_min, x_max = data[:, 0].min() - 1, data[:, 0].max() + 1
y_min, y_max = data[:, 1].min() - 1, data[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
Z = kmeans.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)plt.contour(xx, yy, Z, colors='gray', linewidths=1, alpha=0.5) # 绘制决策边界plt.title('K-means Clustering with Decision Boundaries')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.legend()
plt.show()
本章总结
- 无监督学习的意义
- 聚类的定义
- K-Means方法聚类
- 绘制K-Means决策边界















)


)
