栈、队列、数组、列表
实现方式
队列
class Queue:def __init__(self):self.items = []def enqueue(self, item):self.items.append(item)def dequeue(self):return self.items.pop(0)def empty(self):return self.size() == 0def size(self):return len(self.items)
应用: 约瑟夫斯问题
著名的 约瑟夫斯问题(Josephus Problem)是应用队列(确切地说,是循环队列)的典型案例。
在 约瑟夫斯问题 中,参与者围成一个圆圈,从某个人(队首)开始报数,报数到n+1的人退出圆圈,
然后从退出人的下一位重新开始报数;重复以上动作,直到只剩下一个人为止。值得注意的是,Queue类只实现了简单队列,上述问题实际上需要用循环队列来解决。
在报数过程中,通过“将(从队首)出队的人再入队(到队尾)”来模拟循环队列的行为。具体代码如下:
#!/usr/bin/env python
# -*- coding: utf-8 -*-def josephus(namelist, num):simqueue = Queue()for name in namelist:simqueue.enqueue(name)while simqueue.size() > 1:for i in xrange(num):simqueue.enqueue(simqueue.dequeue())simqueue.dequeue()return simqueue.dequeue()if __name__ == '__main__':print(josephus(["Bill", "David", "Kent", "Jane", "Susan", "Brad"], 3))
20. 有效的括号-栈-简单
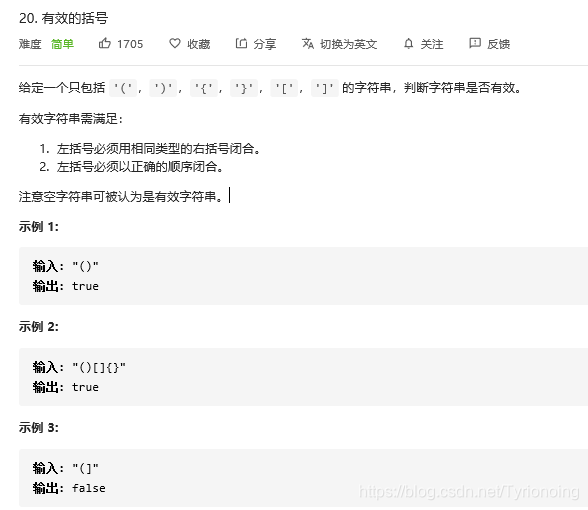
- python自己-实现
class Solution:def isValid(self, s: str) -> bool:# 栈: 遇到 '(', '[', '{'# 词典: {'{}', '()', '[]'}stack = []dict1 = {'}':'{', ']':'[', ')':'('}for i in range(len(s)):if s[i] not in dict1:stack.append(s[i])else:if not stack or stack.pop() != dict1[s[i]]:return Falsereturn False if stack else True
32. 最长有效括号-困难

⭐最长有效括号powcai
⭐手画图解-栈、动态规划 的思路
解题思路一:常规-栈
对于这种括号匹配问题,一般都是使用栈;
先找到所有可以匹配的索引号,然后找出最长连续数列;
例如: s = )(()()), 可以使用栈找到:
位置2 和 位置3 匹配;
位置4 和 位置5 匹配;
位置1 和 位置6 匹配;
这个数组玮 2,3,4,5,1,6 ,这是通过栈找到的,按照递增序列排序,找出该数组的最长连续数列的长度就是最长有小括号长度:
所以复杂度来自于: O ( n l o g n ) O(nlogn) O(nlogn).
接下来思考: 怎么省略排序的过程,在弹栈的时候进行操作呢。
- python实现: 时间复杂度: O ( n ) O(n) O(n);
class Solution:def longestValidParentheses(self, s: str) -> int:if not s:return 0stack = [-1]res = 0for i in range(len(s)):if s[i] == '(':stack.append(i)else:# 这里思路最精彩:# l利用下标存储当前结果; # 通过栈将问题转化为 最大间隔的问题; # 预先设置为 -1, 如果出现先 ) 将 )作为参照物; stack.pop()if not stack:stack.append(i)else:res = max(res, i-stack[-1])return res